采样

统计学或研究中的采样是指从大数据中选择一个子集的方法。在数字通信中，它被定义为以离散形式测量模拟信号的瞬时值的过程。

采样是由采样器执行的过程。它几乎存在于每种类型的数字通信系统中，有助于将模拟信号转换为数字信号。模拟信号是连续的时变信号，而数字信号是离散形式的信号。采样器的功能是测量连续信号的瞬时值的样本，并将其转换为离散值。

在数字通信中，量化器和采样器的组合用作A/D（模拟到数字）转换器。它将输入的模拟信号转换为数字信号。采样器将模拟信号转换为离散值，量化器将每个级别表示为固定的离散有限值集。因此，我们可以将模拟到数字的转换定义为一个两步过程。第一步由采样器执行，第二步由量化器执行。

连续模拟信号和数字信号的波形如下图所示

当以规则的时间间隔对连续信号进行采样，并将其乘以周期性脉冲序列时，产生的信号就是采样信号，如下图所示

在这里，我们将讨论采样定理、采样率、奈奎斯特率、采样方法、抗混叠滤波器、采样的优点、采样的缺点以及采样的应用。

采样定理

采样定理基于固定的采样率，称为奈奎斯特率。因此，采样定理也称为奈奎斯特定理。它基于带限信号的理论。

让我们讨论带通信号和基带信号的采样定理。

根据带通信号的采样理论，如果采样率不大于最大频率W，则可以成功地重建信号。样本之间间隔采样时间“Ts”秒，没有零均方误差。

Ts = 1/2W

根据基带信号的采样理论，如果样本以小于或等于 1/2F_m 的均匀间隔分隔，则可以成功地重建信号。

它可以表示为

Ts ≤ 1/2F_m

采样率

采样率定义为每秒从连续信号中提取的有限值样本的数量。我们也可以将其定义为采样频率，它是采样时间的倒数。

Fs = 1/Ts

其中，

Fs 是采样频率

Ts 是采样时间

如前所述，采样率是采样器执行采样过程的重要时期。它有助于在接收端成功恢复数字信号。因此，为采样率定义了一个固定参数，称为奈奎斯特率。

奈奎斯特率

假设 H 是选择的最高频率。带限信号以低于 W Hz 的频率分量传输。因此，为了复制原始信号，采样率应该是最高频率的两倍。

它由下式给出

F_s = 2W

其中，

F_s 是采样率

W 是最高频率

这种采样率称为奈奎斯特率。以奈奎斯特率采样不会引入任何失真。

奈奎斯特率也称为最小采样率，并用条件表示

Fs = 2Fm

其中，

Fs 是采样频率或采样率

Fm 是输入信号或消息信号的最大频率

奈奎斯特间隔

奈奎斯特间隔是奈奎斯特率的倒数。它由下式给出

T_S = 1/2W

其中，

T_S 是奈奎斯特间隔

W 是最高频率

采样方法

采样方法分类如下

• 理想采样
• 自然采样
• 平顶采样

理想采样

理想采样也称为瞬时采样或脉冲采样。采样过程将输入信号和载波信号相乘，载波信号以脉冲序列的形式存在。

上图显示了消息信号、以脉冲序列形式的采样信号和采样信号的波形。将输入信号和采样信号相乘的工作原理称为乘法原理。

自然采样

自然采样被认为是脉冲幅度调制中一种有效的多路复用方法。这里，模拟信号乘以均匀间隔的矩形脉冲。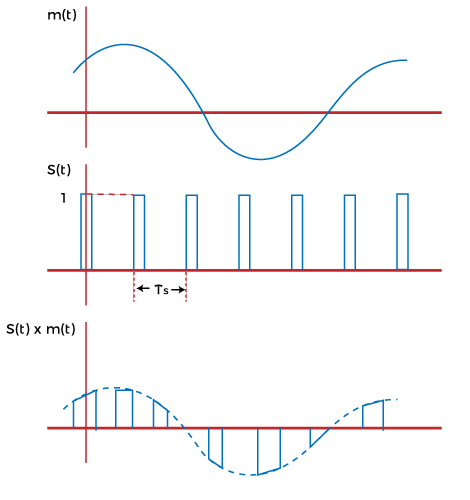

上图显示了消息信号、采样信号和采样信号的波形。

平顶采样

平顶采样的设计和重构比自然采样过程更容易。平顶采样方法中的脉冲在顶部呈扁平形状，并保持在恒定高度。这意味着样本是平坦的并且具有恒定的幅度。

抗混叠滤波器

混叠是在采样过程之后可能产生的常见效应。在混叠过程中，信号中的高频分量会覆盖低频分量。当信号频率超过采样频率的一半 (F_s/2) 时，就会发生混叠。

它可以表示为

Fm > Fs/2

2Fm > Fs

其中，

Fs 是采样频率或采样率

Fm 是输入信号或消息信号的最大频率

类似地，当采样频率超过信号频率的两倍时，可以减少混叠效应。

它表示为

Fs > 2Fm

抗混叠滤波器用于防止传输过程中的混叠效应。此类滤波器的截止频率等于采样率的一半 (F_s/2)。混叠滤波器的功能是从信号中移除和过滤高频分量。它插入在采样器之前。它也被称为低通抗混叠滤波器。通过抗混叠滤波器后的信号以高于奈奎斯特率的速率进行采样。这有助于轻松恢复信号。

为什么需要采样？

我们知道采样过程有助于将模拟信号转换为数字信号。以数字信号形式的数据传输具有各种优点，例如高效率、快速速度、低成本、低干扰、低失真和高安全性。因此，采样对于提高通过通信信道的信号的质量和传输能力至关重要。

采样的优点

采样过程的主要优点是由于传输转换为数字形式，如上所述，数字形式具有各种优点。它将模拟信号转换为离散值。

采样的优点如下

• 成本低
• 高精度
• 易于实现
• 耗时更少
• 信号损耗低
• 范围广

它通过将传入数据转换为适合传输的速率来防止信号损耗或任何信息损耗。例如，如果信号包含高频分量，则采样过程会将其转换为高速率以进行有效传输。通常，输入信号以传入信号频率的两倍的频率采样。这样做是为了保留信号中的完整信息。

采样的应用

采样描述了用于表示样本的可能的数字值的数量。采样至关重要，因为它可以在传输损耗期间防止任何信息丢失。它还可以提高系统的准确性。采样用于各种流程，例如 PAM、PCM 和 TDM。让我们详细讨论采样的应用。

PAM（脉冲幅度调制）

在脉冲幅度调制中，脉冲的幅度随消息信号的采样值而变化。脉冲调制技术广泛用于数字传输，其中非基带应用被 PPM（脉冲位置调制）取代。PAM 调制技术用于各种应用，例如 以太网、电视和 LED 照明。

PCM (脉冲编码调制)

采样器是 PCM 通信系统的重要组成部分，它将模拟信号转换为以二进制数字 0 和 1 形式表示的数字编码信号。它与 量化器 一起使用，它们共同充当模拟到数字转换器。PCM 用于电话网络中，将模拟信号（以音频信号的形式）转换为数字信号，这是在长距离上进行有效传输的首选信号。接收端的数字信号被转换回音频信号，该音频信号在输出端显示为相同的音频信号。

TDM（时分复用）

在 TDM 中，各种信号以相同的频率和相同的速率进行采样，但时间不同。多路复用是一种在同一通信信道上传输多个信号的方法。TDM 中的信号在不同的时间间隔传输，以防止任何串扰或干扰。采样率不同，因为它取决于信号的带宽。TDM 中传输的信号按顺序放置，因为它有助于在接收端轻松恢复信号。

傅里叶变换的重要性

傅里叶变换是表示和分析信号的重要现象。例如，二维傅里叶变换分析有助于从信号中移除高频分量，例如图像信号。它用于各种应用，例如数字传输、信号处理、图像重建、图像压缩、光学和概率。

傅里叶变换的各种特点和优点如下：

• 它提供了信号及其各种域的内部视图。
• 它将信号分解为正弦和余弦分量。
• 它有助于对信号进行平滑分析。
• 它将信号分解为复指数函数的总和。