文氏电桥振荡器

维恩电桥振荡器是一种产生输出正弦波的相移振荡器。 维恩电桥振荡器以 Max Karl Wien 的名字命名，该电路基于 1890 年代开发的电桥电路。 它是最简单的振荡器之一，以其在音频方面的应用而闻名。

构建

维恩电桥振荡器包括两个电容器（储能元件）和四个电阻器。该电路的另一个组成部分是反相放大器，如运算放大器或晶体管。 在这里，该电路使用了两个晶体管。 该电路中的两个组合是一个串联组合和一个 RC 的并联组合。

维恩电桥振荡器的电路如下图所示

它有两条反馈路径，正反馈和负反馈。

振荡频率

振荡频率由下式给出

当电阻器和电容器都具有相同值时，振荡频率由下式给出

R1 = R2 = R

C1 = C2 = C

电阻器和电容器 R1、R2、C1 和 C2 形成一个带通滤波器。

推导

推导将为我们提供持续振荡的条件。 这是克服维恩电桥振荡器缺点的其中一种方法。 维恩电桥振荡器的等效电路图可以表示为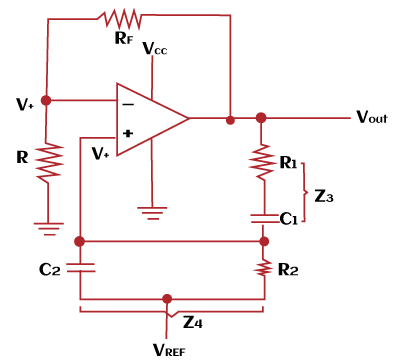

Z1 = R

Z2 = R_F

Z3 = (R₁ + 1/sC₁)

Z4 = (R₂ || 1/sC₂)

其中，

Z 是阻抗

R_F 是反馈电阻

(R₁ + 1/sC₁) 是 R₁ 和 C₁ 的串联组合。

(R₂ || 1/sC₂) 或 [(R₂/(1 + R₂sC₂)) 是 R₂ 和 C₂ 的并联组合

正反馈电压 (V+) 连接到放大器的同相端。 它由下式给出

V+ = V_O [Z4 (Z3 + Z4)]

V+ = V_O [(R₂/1 + R₁sC₂) / ((R₂/1 + R₂sC₂ + R₁ + 1/sC₁))]

B = V+ / V_O = 1/ (1 + R₁sC₂ + R₁/ R₂ + 1/ R₂sC₁ + C₂/ C₁)

设，s = jω_o (ω_o 是振荡频率)

令 ω₁ = 1/ R₁C₂ 和 ω₂ = 1/ R₂C₁ 的值相等，我们得到

B = V+ / V_O = 1/ (1 + R₁/ R₂ + C₂/ C₁ + j (ω_o/ ω₁ - ω₂/ ω_o))

电容器和电阻器可以产生总共 180 度的相移，这由振荡频率提供。 如前所述，单个 RC 网络提供最大 90 度的相移。 因此，两个 RC 网络可以贡献最大 180 度的相移。

为了找到整体反馈，我们假设，

R1 = R2 = R C1 = C2 = C，且 ω₁ = ω₂ = ω_o

反馈由下式给出

B = 1/ (1 + R/ R + C/ C + j (ω_o/ ω_o - ω_o / ω_o))

B = 1/ (1 + R/ R + C/ C +0)

B = 1/ (1 + 1 + 1)

B = 1/ 3

如果 AB = 1

B = 1/3

增益将为 (A) = 3

来自电路的反馈可以表示为

B = 1 + R_F/R

3 = 1 + R_F/R

R_F/R = 2

R_F = 2R

这是维恩电桥振荡器持续振荡的条件。

它指出，幅度和反馈的乘积是一。 振荡器的总反馈经过计算以确保正反馈，即相移为 0 或 360 度。 它进一步维持系统的周期性振荡。 持续振荡基于 Barkhausen 准则。

相移

在 RC 相移振荡器的情况下，正反馈（0 或 360 度）的总相移由反馈路径和放大器处的相网络利用。 但是，在维恩电桥振荡器的情况下，两个晶体管分别提供 180 度的相移。

因此，确保正反馈的总相移为

相移 = 180 (晶体管) + 180 (晶体管)

相移 = 360 度

相移 = 360 度 = 0 度

维恩电桥振荡器的输出和相移图如下图所示

上图表明，在低频时相移为正，而在高频时相移为负。 负相移会产生相延迟。 在图的中间，确定共振频率，由下式给出

如上推导中所讨论的，输出电压等于输入电压的 1/3，以允许振荡发生。

历史

• 1891 年，德国物理学家Max Karl Wien 开发了一种电桥电路来测量阻抗。 后来开发的振荡器基于 Karl Wien 电桥电路。
• 1937 年，基于电桥电路开发了灯丝灯和音频振荡器。
• 1937 年至 1938 年，Terman、Bill Hewlett（惠普联合创始人）和 R. R. Buss 之间就振荡器的负反馈进行了各种讨论。 然后，振荡器首先在波兰进行了演示。
• Bill Hewlett 的第一款产品 HP 200A 在加利福尼亚制造，是一种精确的维恩电桥振荡器。
• Hewlett 的振荡器可以产生正弦波形式的输出，具有较小的失真和稳定的幅度。

优点

维恩电桥振荡器的优点如下

• 它是一个简单的电路。
• 它提供恒定的输出。
• 由于存在两个晶体管，因此它产生高增益。
• 电位器可与振荡器一起使用以更改振荡频率。
• 良好的频率稳定性。
• 低失真。
• 它提供易于调谐的优势。

缺点

维恩电桥振荡器的缺点如下

• 它可能导致高输出失真。
• 它不能产生高频。
• 由于有两个晶体管，因此它具有大量的组件。

数值例子

让我们讨论两个基于维恩电桥振荡器的例子。

示例：1 在维恩电桥振荡器中，R1 = 10k 欧姆，R2 = 5k 欧姆，X_C1 = 10k 欧姆，X_C2 = 5k 欧姆。 求电路的两个阻抗。

解决方案：给定： R1 = 10k 欧姆 = 10⁴ 欧姆

R2 = 5k 欧姆 = 5 x 10³ 欧姆

XC₁ = 10k 欧姆 = 10⁴ 欧姆

XC₂ = 5k 欧姆 = 5 x 10³ 欧姆

X 是电抗，定义为电阻和共振共同作用产生的、阻碍电流的效应。 维恩电桥振荡器中有两个阻抗，串联和并联。 设两个阻抗为 Z1 和 Z2。

Z1 = R1 + X_C1 = 20k 欧姆

1/Z2 = 1/R2 + 1/ X_C2

1/Z2 = 1/5000 + 1/5000

1/Z2 = 2/5000

Z2 = 2500 欧姆 = 2.5k 欧姆

因此，电路的两个阻抗为 20k 欧姆和 2.5k 欧姆。

示例：2 在维恩电桥振荡器中，R1 = R2 = 100k 欧姆，C1 = C2 = 200 p 法拉。 求电路振荡的频率。

解决方案：给定： R1 = R2 = 100k 欧姆 = 100 x 10³ 欧姆 = 10⁵ 欧姆

C1 = C2 = 200 pF = 200 x 10^-12 法拉 = 2 x 10^-10 法拉

可以使用以下公式计算振荡频率

F = 1/ (2 x 3.1415 x 10⁵ x 2 x 10^-10)

F = 10⁵/ 12.566

F = 7958 赫兹

因此，振荡频率为 7958 赫兹或 7.958k 赫兹。