TensorFlow Playground

2024年11月14日 | 阅读7分钟

TensorFlow Playground 是一个用 d3.js (JavaScript) 编写的 Web 应用程序。它是学习神经网络 (NN) 而无需数学的最佳应用程序。在我们的 Web 浏览器中，我们可以创建一个 NN（神经网络） 并立即查看结果。它已获得 Apache 2.0 许可，2004 年 1 月 (https://apache.ac.cn/licenses/)。

Daniel Smilkov 和 Shan Carter 创建了它，并基于许多先前作品的延续。它的贡献成员是 Fernanda Viegas 和 Martin Wattenberg 以及 Big Picture 和 Google Brain 团队，以提供反馈和指导。

TensorFlow Playground 是一个 Web 应用程序，允许用户使用 TensorFlow 机器学习库测试人工智能 (AI) 算法。

TensorFlow Playground 不熟悉高级数学和使用神经网络进行深度学习和其他机器学习应用程序的编码。神经网络操作是交互式的，并在 Playground 中表示。

该开源库专为教育需求而设计。

现在转到链接 http://playground.tensorflow.org。

网站的顶部是 Epoch、学习率、激活、正则化率、问题类型， 这些将在下面逐一描述。

每次对训练集进行训练时，Epoch 数量都会增加，如下所示。

学习率决定了学习的速度；因此，我们需要选择合适的学习率。

节点的 激活函数 定义了该节点或一组数据的输出。标准计算机芯片电路可以是数字 激活函数 的网络，它可以是“ON”（1）或“OFF”（0），具体取决于其输入。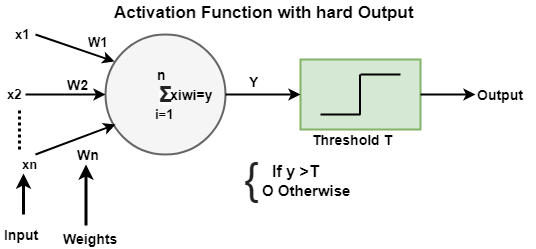

软输出激活函数

ReLU （修正线性单元） g(y) = max(0,y)
Tanh (双曲正切) t(y) =
Sigmoid （逻辑 Sigmoid） σ(y) =
线性（例如，α=1） l(y)= αy

正则化 用于避免过度拟合。

TensorFlow playground 实现了两种类型的正则化：L1、L2。

正则化可以增加或减少固定或弱连接的权重，以使模式分类更清晰。

L1 和 L2 是流行的正则化方法。

L1 正则化

L1 在稀疏特征空间中很有用，在这种空间中，需要在众多特征中选择少数特征。
L1 将进行选择并分配重要的权重值，并将未选择的权重设置为很小（或零）

L2 正则化

L2 适用于相关输入
L2 将控制权重值，使其与相关性水平相同。

Dropout 也是一种正则化方法。

较高的 正则化率 将使权重的范围更有限。

在问题类型中，从以下两种类型的问题中选择

分类
回归

我们必须根据我们在这里指定的数据集来查看我们要解决的问题的类型。根据我们在下面定义的数据集解决。

总共有四种分类类型，以及两种回归问题类型，如下所示。

此处蓝色和橙色点形成数据集，这意味着

橙色点的值为 -1。蓝色点的值为 +1

使用训练测试数据的比率，可以使用此处的控制模块控制训练集的百分比。

例如：如果为 50%，则点与默认设置相同，但如果我们将控制更改为 10%。那么我们可以看到那里的点变得不那么像给定的图了。

可以控制数据集的噪声水平。我们可以使用控制模块来做到这一点。随着噪声的增加，数据模式变得更加不可靠。当噪声为零时，问题在其区域中被清楚地区分。但是，通过将其设置为 50，我们可以看到蓝色点和橙色点都混在一起了，并且强制分配。

批处理大小决定了用于每次训练迭代的数据速率，我们根据下面的屏幕截图来控制它。我们可以使用以下方法控制它。

现在，我们需要进行特征选择。 特征选择将使用此处给出的 x1 和 x2；

X1 是横轴上的值。
X2 是纵轴上的值。

x1 和 x2 的示例 - 该点大约有一个 x1 值 3.1 和 x2 值 4，就像我们可以在下面的图表中看到的那样。

隐藏层结构如下所示，我们最多可以设置六个隐藏层。如果我们想通过添加隐藏层来控制隐藏层的数量，请单击加号。并且我们也可以在每个隐藏表中添加最多八个神经元，并通过单击加号来控制此操作，以便向隐藏层添加神经元。

按下箭头按钮开始 NN（神经网络） 训练，其中 Epoch 将增加 1，并且 反向传播 用于训练神经网络。如果我们需要刷新整个实践，那么我们可以通过单击刷新按钮来做到这一点。

NN（神经网络） 最小化 测试损失 和 训练损失。测试损失和训练损失的变化将显示在右侧下方的小性能曲线中。测试损失将有一个白色性能曲线，而训练损失将有一个灰色性能曲线。如果损失减少，曲线将下降。

神经网络模型/感知器

神经网络模型或感知器是一个由称为神经元的简单组件组成的网络，这些神经元接收输入，根据数据更改其内部状态。并根据数据和激活生成输出（0 和 1）。我们只有一个输入和输出，最多一个隐藏层，在最容易访问的神经网络中称为 浅层神经网络。

Playground 中的所有颜色含义

橙色和蓝色用于不同的可视化，但在真实世界中，橙色显示负值，蓝色显示正值。

数据点被涂成橙色或蓝色，这对应于正数和负数。

在隐藏层中，线条的颜色由神经元之间连接的权重决定。蓝色显示实际权重，橙色显示负权重。

在输出层中，点根据原始值着色为橙色或蓝色。背景颜色显示网络正在预测特定区域的内容。

用例

为什么我们可以在隐藏层中增加神经元？

我们可以从隐藏层中的单个神经元的基本模型（浅层神经网络）开始。让我们选择数据集“Circle”，特征“X1”和“X2”，0.03 学习率和“ReLU”刺激。

我们将按下运行按钮并等待一百个 epoch 完成，然后单击“暂停”。

在完成 100 个 epoch 后，训练损失和测试损失超过 0.4。现在，我们将使用添加按钮在隐藏层中添加四个神经元，然后再次运行。

现在，我们的测试和训练损失为 0.02，并且输出在两个类别（橙色和蓝色）中被很好地分类。在隐藏层中添加神经元提供了分配不同权重和并行计算的灵活性。但是，在某个程度上添加神经元会付出高昂的代价，但收益甚微。

为什么我们在分类问题中使用非线性激活函数？

在神经网络中，我们使用非线性激活函数来解决分类问题，因为我们的输出标签在 0 到 1 之间，而线性激活函数可以提供 -∞ 到 +∞ 之间的任何数字。结果，输出不会在任何时候收敛。

在上图中，我们运行了相同的模型，但使用线性激活，并且它没有收敛。在 100 个 epoch 之后，测试和训练效率超过 0.5。

为什么我们可以在 Playground 中增加隐藏层？

现在，我们添加了一个带有双神经元的隐藏层，并按下了运行按钮。我们的测试和精度在 50 个 epoch 中降低到 0.02 以下，几乎是任何单个隐藏层模型的一半。与神经元类似，为所有情况添加隐藏层将不是正确的选择。它会变得昂贵，而没有任何好处。这一点在图中得到了很好的解释。即使运行 100 个 epoch，我们也无法获得良好的结果。