Moore 机

摩尔机是一种有限状态机，其中下一个状态由当前状态和当前输入符号决定。 给定时间的输出符号仅取决于机器的当前状态。 摩尔机可以用 6 个元组 (Q, q0, ∑, O, δ, λ) 描述，其中，

示例 1

摩尔机的状态图是

摩尔机的转换表是

在上面的摩尔机中，输出用每个输入状态表示，并用 / 分隔。 摩尔机的输出长度比输入大 1。

输入 010

转换: δ (q0,0) => δ(q1,1) => δ(q1,0) => q2

输出: 1110(q0 为 1，q1 为 1，q1 再次为 1，q2 为 0)

示例 2

设计一个摩尔机来生成给定二进制数的 1 的补码。

解决方案: 要生成给定二进制数的 1 的补码，简单的逻辑是如果输入为 0，则输出为 1，如果输入为 1，则输出为 0。这意味着有三种状态。 一种状态是起始状态。 第二种状态是将 0 作为输入并产生 1 作为输出。 第三种状态是将 1 作为输入并产生 0 作为输出。

因此，摩尔机将是，

例如，取一个二进制数 1011，然后

因此，我们得到 00100 作为 1011 的 1 的补码，我们可以忽略初始 0，我们得到的输出是 0100，它是 1011 的 1 的补码。 交易表如下

因此摩尔机 M = (Q, q0, ∑, O, δ, λ); 其中 Q = {q0, q1, q2}, ∑ = {0, 1}, O = {0, 1}。 转换表显示了 δ 和 λ 函数。

示例 3

为二进制输入序列设计一个摩尔机，如果它有一个子串 101，机器输出 A，如果输入有一个子串 110，它输出 B，否则它输出 C。

解决方案: 为了设计这样的机器，我们将检查两个条件，即 101 和 110。如果我们得到 101，输出将是 A，如果我们识别 110，输出将是 B。对于其他字符串，输出将是 C。

部分图将是

现在我们将插入每个状态的 0 和 1 的可能性。 因此，摩尔机变为

示例 4

构造一个摩尔机，确定输入字符串是否包含偶数或奇数个 1。 如果字符串中有偶数个 1，机器应给出 1 作为输出，否则给出 0。

解决方案

摩尔机将是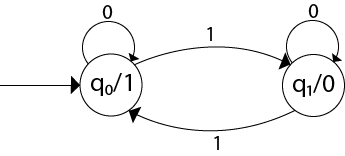

这是所需的摩尔机。 在这台机器中，状态 q1 接受奇数个 1，状态 q0 接受偶数个 1。 对零的数量没有限制。 因此，对于 0 输入，自环可以应用于两种状态。

示例 5

设计一个输入字母 {0, 1} 和输出字母 {Y, N} 的摩尔机，如果输入序列包含 1010 作为子字符串，则产生 Y 作为输出，否则产生 N 作为输出。

解决方案

摩尔机将是