GATE || GATE-CS-2014 (Set 1)17 Mar 2025 | 51 分钟阅读 1) 下列哪个选项与下面句子中带下划线的短语意思最接近? 看到生命形式适应各种环境条件,真是令人着迷。
答案: B 解释:在上面的短语中,带下划线的部分是 *cope with*。 “Cope” - 这是一个动词。 “adopt” - 动词。 “adapt” - 动词。 “adept” - 形容词 “accept” - 动词 因此,只有“adapt”符合问题中所描述的短语。 2) 选择下面选项中最合适的词来完成以下句子。 他无法理解法官授予她一等奖,因为他认为她的表演相当。 。 。 。 。 。 。 。 。 。 。
答案:C 解释:在这里,superb 和 exhilarating 都意味着表演很出色。但是,他无法理解她为什么获得一等奖这一事实表明,他认为她的表演并不那么令人印象深刻。所以 A 和 D 是错误的。 Medium 通常用作名词,表示质量、价值等的中等水平。所以 B 是错误的 Mediocre 用作形容词(表示质量),意思是表现平平,即普通,不非凡。所以 C 是正确选项。 3) 在关于近期丑闻的新闻发布会上,部长说:“责任到此为止”。部长通过这句话传达了什么?
答案:C 解释:“The buck stops here”(责任到此为止)的意思是 - 责任不会超出此点。 选项(C)是正确的。 4) IF (z + 1 / z)2 = 98,计算 (z2 + 1 / z2)
答案: A 解释: (z + 1 / z)2 = (z2 + 1 / z2) + 2 * z * 1 / z (z2 + 1 / z2) = (z + 1 / z)2 - 2 = 98 - 2 = 96 5) ax2 + bx + c 的根是实数且为正。a、b 和 c 是实数。那么 ax2 + b|x| + c 有
答案: D 解释:第二个方程具有第一个方程根的正值和负值。 6) 帕尔加特山口(或帕拉卡德山口)是印度西部盖茨山脉南部一个约 30 公里宽的地区,比其南北的山地低。形成这个山口的确切原因尚不清楚。它导致泰米尔纳德邦邻近地区从西南季风获得更多降雨,而喀拉拉邦邻近地区夏季气温更高。从这段文字可以推断出什么?
答案:C 解释:这里的问题是,“可以推断出什么?”也就是说,它询问的是这段文字隐藏的结论。 为什么不是选项 A?- 因为这段文字清楚地说明了:“形成这个山口的确切原因尚不清楚。” 为什么不是选项 B?- 因为这段文字没有谈论泰米尔纳德邦和喀拉拉邦靠近帕尔加特山口的低洼地区。 为什么不是选项 D?- 因为这段文字只说:“喀拉拉邦邻近地区夏季气温更高”,并没有说这种高温会导致降雨。 注意:我们必须根据文字中给出的信息进行思考和得出结论。我们不能自己下结论。为什么选项 C?- 因为这段文字说:“它导致泰米尔纳德邦邻近地区从西南季风获得更多降雨,而喀拉拉邦邻近地区夏季气温更高。” 因此,选项 C 是正确的。 7) 遗传学家说,他们非常接近确认精神疾病(如抑郁症和精神分裂症)的遗传根源,因此,医生将能够通过早期识别和基因疗法根除这些疾病。 上述陈述依赖于以下哪项假设?
答案: B 说明
所以,B 是正确选项。 8) 前往旅游目的地的往返机票可享受总票价 10% 的折扣。此外,4 人或 4 人以上团体可享受总票价 5% 的折扣。如果单程单人票价为 100 卢比,那么 5 名游客购买往返机票的总费用为 卢比。 . . . . . . . . . . . . . . .
答案:a 解释:单程单人票价为 100。因此,往返票价为 200。 5 人为 200 x 5 = 1000 现在第一个折扣是总票价的 10%,即 100(1000 的 10%)。并且由于团体人数超过 4 人,总票价可额外享受 5% 的折扣,即 50(1000 的 5%)。 因此总折扣为 100 + 50 = 150。 因此,机票价格为 1000 - 150 = 850 卢比。 9) 在一项调查中,向 300 名受访者询问他们是否拥有车辆。如果拥有,他们会被进一步要求说明他们拥有汽车还是踏板车,或者两者都拥有。他们的回应如下表所示。  不拥有踏板车的受访者百分比是多少?
答案:a 解释:不拥有踏板车的受访者人数 = 仅拥有汽车的人数 + 两人都不拥有的人数。 男性中有 40 + 20 = 60,女性中有 34 + 50 = 84。 总计 60 + 84 = 144。 现在百分比为 (144 / 300) *100 = 48 10) 当一个点连接到四面体(具有四个三角形表面)的顶点时,会产生多少(新的)内部平面? . . . . . . . . . . . . . . . . . . . .
答案:a 解释:四面体有 4 个三角形表面,4 个顶点/角(假设为 A、B、C 和 D)。现在,如果您取四面体内的任意一点(假设为 O)并将其与任意两个顶点(假设为 A 和 B)连接,您将得到 1 个内部平面,即 OAB。 因此,我们可以从这里看出,新内部平面的数量 = 不同顶点对的数量。 同样,您可以选择任意其他 2 个顶点,如 (A, C) 或 (A, D) 或 (B, C) 或 (B, D) 或 (C, D)。 我们也可以使用组合公式来计算可能的顶点对, 11) 考虑陈述 并非所有闪闪发光的都是金子。 谓词 glitters(x) 在 x 闪闪发光时为真,谓词 gold(x) 在 x 是金子时为真。以下哪个逻辑公式代表上述陈述? 
答案:d 解释:陈述“并非所有闪闪发光的都是金子”可以表示如下 ¬(∀x(glitters(x)⇒gold(x)). . . . . . . . . . . . . . . . . . (1) 其中 ∀x(glitters(x)⇒gold(x) 表示所有闪闪发光的都是金子。现在, ∃x¬(glitters(x)⇒gold(x)) . . . . . . . . . . . . . . . . . . . . . . .(2) , 因为我们知道 ¬∀x() = ∃x¬() (其中 ∀ 表示 -> 所有,∃x 表示 -> 存在某些)。 我们知道,A⇒B 仅在 A 为假或 B 为真时才为真。它也可以用另一种方式定义 A⇒B=¬A∨B(非A 或 B) . . . . . . . . . . . . . . . . . . . . . . .(3) 从方程 (2) 和 (3) 中,我们有 ⇒∃x(glitters(x)∧¬gold(x)) . . . . . . . . . . . . . . . . . . . . (4) , 非否定消除 ¬(¬) = () : and ¬(()∨()) = (¬()∧¬()) . 所以答案是 (D)。 12) 假设您在随机选择的单位长度的木棍上将其折断。那么较短木棍的期望长度是 . . . . . . . . . . . .
答案:a 解释:较短的木棍长度范围从几乎 0 单位到最多 0.5 单位,每种长度的可能性均等。 因此,平均长度约为 (0 + 0.5) / 2 = 0.25 单位,这是答案。 13) 令 G=(V,E) 为一个有向图,其中 V 是顶点集,E 是边集。那么以下哪个图与 G 具有相同的强连通分量? 
答案:b 解释:如果我们反转图中所有弧的方向,新图将具有与原始图相同的强连通分量集。 14) 考虑以下方程组 3x + 2y = 1 4x + 7z = 1 x + y + z = 3 x - 2y + 7z = 0 该方程组的解的数量是 . . . . . . . . . . . . . .
答案:a 解释: rank(增广矩阵) = rank(矩阵) = 未知数数量。 因此它有一个唯一的解。 15) 4x4 对称正定矩阵任意一对不同特征值对应的特征向量的点积的值是 . . . . . . . . . . . . . . .
答案:a 解释:实对称矩阵不同特征值对应的特征向量相互正交。正交向量的点积为 0。 16) 
答案:c 解释:在给定的问题中,⊝的范围从 π / 6 到 π/ 3。 当 ⊝=π / 6 时,函数的值为 0,因为行 1 和行 2 相同。 当 ⊝ = / 3 时,函数的值为 0,因为行 1 和行 3 相同。  由于它是三角函数,因此该函数在给定范围内是连续且可微的。 那么根据微分中值定理, 存在一个值 c 使得 f'(c) = 0。因此第一个陈述是正确的。 也可能存在一个值 c,使得 f'(c) ? 0。这是因为该函数不是常数函数,即范围内的所有值都不等于 c。 因此第二个陈述也是正确的。 因此正确选项是 C。 17) 考虑以下布尔表达式 F F(P, Q, R, S) = PQ + P'QR + P'QR'S F 的最小积之和形式是
答案:a 解释:给定, F(P, Q, R, S) = PQ + P'QR + P'QR'S = Q(P + P'R + P'R'S) = Q(P + R + R'S) = Q(P + R + S) = PQ + QR + QS 注意 A + AB = A 和 A + A'B = A + B。 所以,选项 (A) 是正确的。 18) 使得以下方程成立的数制(或基数)是 . . . . . . 312/20 = 13.1
答案:c 解释:设 x (≠ 0) 为给定方程的基数。 我们有, LHS = ( 3x2 + x + 2 ) / ( 2x) = ( 3x / 2 ) + ( 1 / 2 ) + ( 1 / x ) RHS = x + 3 + ( 1 / x ) 现在,为了使方程成立,LHS = RHS ( 3x / 2 ) + ( 1 / 2 ) + ( 1 / x ) = x + 3 + ( 1 / x ) ⇒ 3x + 1 = 2x + 6 ⇒ x = 5 所以,基数是 5。 19) 考虑以下 C 语言程序 以下哪个陈述是正确的?
答案:d 解释:程序没有问题,因为 pi 指向一个有效的位置。 另外,在 scanf() 中我们传递变量的地址,而 pi 是一个地址。 20) 令 G 为一个有 n 个顶点和 m 条边的图。深度优先搜索 G 的运行时间的紧密上界是什么?假设图使用邻接矩阵表示。
答案:c 解释:当图使用邻接表表示时,深度优先搜索需要 O(m + n) 时间。 在邻接矩阵表示中,图被表示为“n x n”矩阵。为了进行 DFS,对于每个顶点,我们遍历该顶点对应的行以查找所有相邻顶点(在邻接表表示中,我们只遍历顶点的相邻顶点)。因此时间复杂度变为 O(n2) 21) 考虑使用指针表示的根二叉树。确定具有正好 4 个节点的子树所需时间的最佳上界是 O(na Logn b)。那么 a + 10b 的值是 . . . . . . . .
答案:a 解释:我们可以在 O(n) 时间内找到有 4 个节点的子树。以下是一个简单的方法。 1) 以自底向上的方式遍历树,并找到以当前节点为根的子树的大小。 2) 如果大小为 4,则打印当前节点。 以下是 C 实现 22) 考虑下面的有向图。以下哪个是正确的? 
答案:c 解释:该图不包含任何循环,因此存在拓扑排序。 P 和 S 必须出现在 R 和 Q 之前,因为 P 到 R 和 Q 有边,S 到 R 和 Q 有边。 23) 令 P 为一个使用第一个元素作为枢轴对数字进行升序排序的快速排序程序。令 t1 和 t2 分别是 P 对输入 {1, 2, 3, 4, 5} 和 {4, 1, 5, 3, 2} 进行比较的次数。以下哪个成立?
答案:c 解释:当选择第一个或最后一个元素作为枢轴时,快速排序的最坏情况发生在已排序的数组上。 在快速排序的每一步中,数字按以下递推关系划分。 T(n) = T(n - 1) + O(n) 24) 以下哪个是正确的? 
答案:c 解释:(A) L = {a n b n |n >= 0} 不是正则语言,因为不存在一个有限自动机可以推导出这个文法。直观地说,有限自动机只有有限的内存,因此它无法跟踪状态的数量。它是标准的上下文无关语言。 (B) L = {a n b n |n 是素数} 仍然不是正则语言,因为没有办法记住/检查当前的 n 是否为素数。因此,不存在有限自动机来推导这个文法,所以它 (C) L = {w|w 包含 3k+1 个 b} 是正则语言,因为 k 是一个固定常数,我们可以轻松地将 L 模拟为 a ∗ba∗ . . . . . . . . . ba∗,使得有正好 3k + 1 个 b,并且在 D) L = {ww | w ∈ Σ ∗ } 不是正则文法,事实上它甚至不是 CFG。没有办法使用有限自动机来记住和推导双倍单词。 因此,正确答案是 (C)。 25) 
答案:a 说明  因此,对于输入字符串 0011,q0、q1 和 q2 是可达状态,但 q3 不是。 所以,选项 (A) 是答案。 26)一台机器具有 32 位架构,指令长度为 1 字。它有 64 个寄存器,每个寄存器长 32 位。它需要支持 45 条指令,这些指令除了两个寄存器操作数外,还有一个立即数操作数。假设立即数操作数是无符号整数,立即数操作数的最大值是 . . . . . . . .
答案:a 解释:1 字 = 32 位 每条指令有 32 位。为了支持 45 条指令,操作码必须包含 6 位。 寄存器操作数 1 需要 6 位,因为寄存器总数为 64。寄存器操作数 2 也需要 6 位。因此,所有 45 条指令和两个寄存器操作数总共需要 18 位。所以, 32-18 = 14 剩下 14 位用于立即数操作数,现在 2^14 - 1 = 16383 我们可以给出最大值 16383。 27) 以下哪个是错误的?
答案:d 解释:(A) 基本块是指令序列,控制在序列的开头进入,在结尾退出,这是正确的。 (B) 可用表达式分析可用于公共子表达式消除,这是正确的。可用表达式是一种分析算法,它确定程序中每个点的表达式集合,这些表达式无需重新计算。可用表达式分析用于全局公共子表达式消除 (CSE)。如果在某一点表达式可用,则无需重新评估它。 (C) 活动变量分析可用于死代码消除,这是正确的。 (D) x = 4 * 5 => x = 20 是公共子表达式消除的一个例子,这是错误的。 公共子表达式消除 (CSE) 指的是编译器优化,当有益时,用保存计算值的单个变量替换相同的表达式(即它们都计算为相同的值)。 以下是一个例子 在以下代码中 a = b * c + g; d = b * c * e; 可以考虑将代码转换为 tmp = b * c; a = tmp + g; d = tmp * e; 28) 匹配以下项 
答案:b 说明
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
29) 假设有一个磁盘有 201 个磁道,编号从 0 到 200。在某个时间,磁盘臂位于磁道 100,并且有一系列磁盘访问请求,请求的磁道是 30、85、90、100、105、110、135 和 145。如果使用最短寻道时间优先 (SSTF) 进行磁盘访问调度,则为磁道 90 的请求将在服务了 . . . . . . . . . . . . . . . . . . 2 个请求后服务。
答案:c 解释:在最短寻道时间优先算法中,首先处理最接近磁盘臂和磁头当前位置的请求。 在本题中,磁臂当前位于磁道号 100。现在,请求按顺序出现在磁道号 30、85、90、100、105、110、135 和 145 的队列中。 磁盘将首先服务其磁道号最接近其磁臂的请求。因此,第一个服务的请求是磁道号 100(因为磁臂本身就指向它),然后是 105,然后是 110,然后磁臂来服务磁道 90 的请求。因此,在服务磁道 90 的请求之前,磁盘将已经服务了 3 个请求。 因此选项 C。 30) 以下哪个是错误的?
答案:d 说明
31) 考虑关系模式 R = {E, F, G, H, I, J, K, L, M, N} 和 R 上的函数依赖集 {{E, F} -> {G}, {F} -> {I, J}, {E, H} -> {K, L}, K -> {M}, L -> {N}}。R 的键是什么?
答案:b 说明 所有属性都可以从 {E, F, H} 推导出来。 要解决这些经常在 GATE 试卷中出现的问题,请尝试使用捷径来节省足够的时间。 第一种方法 使用给定的选项,尝试获得每个选项的闭包。解决方案是包含 R 并且是最小超键,即候选键的那个。 A) {E, F}+ = {E, F, G, I, J} ≠ R(给定的关系)B) {E, F, H}+ = {E, F, G, H, I, J, K, L, M, N} = R(正确,因为确定了给定关系的每个成员)C) {E, F, H, K, L}+ = {E, F, G, H, I, J, K, L, M, N} = R(不正确,尽管给定关系的每个成员都可以确定,但它不是最小的,因为根据候选键的定义,它应该是最小的超键)D) {E}+ = {E} ≠ R 第二种方法 因为,{E, F, G, H, I, J, K, L, M, N}+ = {E, F, G, H, I, J, K, L, M, N}{E, F, G, H, I, J, K, L, M}+ = {E, F, G, H, I, J, K, L, M, N}(因为 L -> {N},所以可以用 L 替换 N)以类似的方式,K -> {M} 所以用 K 替换 M{E, F, G, H, I, J, K, L}+ = {E, F, G, H, I, J, K, L, M, N} 再次 {E, F, G, H, I, J}+ = {E, F, G, H, I, J, K, L, M, N}(因为 {E, H} -> {K, L},所以用 EH 替换 KL){E, F, G, H}+ = {E, F, G, H, I, J, K, L, M, N}(因为 {F} -> {I, J} ){E, F, H}+ = {E, F, G, H, I, J, K, L, M, N}(因为 {E, F} -> {G} ) 32) 考虑以下两个陈述 S1:可以用等效的 Check 断言在 SQL 中替换外键声明。 S2:给定表 R(a,b,c),其中 a 和 b 共同构成主键,以下是一个有效的表定义。 以下哪个陈述是正确的?
答案:d 解释:检查断言不足以替换外键。外键声明可能有级联删除,这仅通过检查插入是不可能的。 使用检查条件,我们可以在向子表添加元素时获得与外键相同的影响。但是,当我们从父表中删除元素时,引用完整性约束不再有效。因此,检查约束无法替换外键。 所以,我们不能用一个检查来替换它。 S2:给定表 R(a, b, c),其中 a 和 b 共同构成主键,以下是一个有效的表定义。 False 一个表中的外键应唯一标识另一个表中的行。在上表定义中,表 S 有一个外键引用 R 的字段 'a'。表 S 中的字段 'a' 不能唯一标识 R 表中的行。 33) 考虑以下关于链路状态和距离向量路由协议的三个陈述,用于具有 500 个网络节点和 4000 个链路的大型网络。 [S1] 链路状态协议的计算开销高于距离向量协议。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - [S2] 距离向量协议(带水平分割)可避免持久性路由循环,但链路状态协议则不能。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - [S3] 在拓扑结构更改后,链路状态协议的收敛速度比距离向量协议快。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 以下关于 S1、S2 和 S3 的哪个是正确的?
答案:d 说明 链路状态 每个节点收集完整的图结构,每个节点计算到它的最短路径,每个节点生成自己的路由表。 距离向量没有一个节点拥有图的副本,节点通过迭代构建自己的表,每个节点将表信息发送给邻居 [S1] 链路状态协议的计算开销高于距离向量协议。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - [S2] 距离向量协议(带水平分割)可避免持久性路由循环,但链路状态协议则不能。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - [S3] 在拓扑结构更改后,链路状态协议的收敛速度比距离向量协议快。 S1 显然是真的,因为在链路状态协议中,所有节点都计算整个网络图的最短路径。 S3 也是真的,因为距离向量协议存在“计数到无穷”问题并且收敛速度较慢。 S2 是假的。在距离向量协议中,带毒逆转的水平分割可以减少形成循环的可能性,并使用最大跳数来对抗“计数到无穷”问题。这些措施在某些情况下可以避免路由循环的形成,但并非在所有情况下。 34) 以下哪些用于通过网络安全协议生成消息摘要? (P) RSA (Q) SHA-1 (R) DES (S) MD5
答案:c 说明
Q 和 S,即 SHA 1 和 MD5,用于通过网络安全协议生成消息摘要。 所以,C 是正确选项。 35) 确定 Web 浏览器和 Web 服务器之间交互中发生以下操作的正确顺序。 1. Web 浏览器使用 HTTP 请求一个网页。 2. Web 浏览器与 Web 服务器建立 TCP 连接。 3. Web 服务器使用 HTTP 发送请求的网页。 4. Web 浏览器使用 DNS 解析域名。
答案:a 解释:Web 浏览器首先需要使用 DNS 从 URL 中找出站点的 IP 地址,然后建立一个 TCP 连接,通常是在端口 80 上。一旦建立 TCP 连接,浏览器就使用 GET 发送 HTTP 请求。最后,Web 服务器以 HTTP 响应进行响应。 36) 考虑一个长度为 2 公里、有 10 个站(包括一个监控站)的令牌环网络。信号传播速度为 2 × 108 m/s,且忽略令牌传输时间。如果每个站允许持有令牌 2 μsec,那么监控站在假定令牌丢失之前应等待的最短时间(以 μsec 为单位)是 . . . . . . . . . .
答案:a 说明 长度 = 2 公里 传播速度 v = 2 * 10^8 m/s 令牌持有时间 = 2 微秒 等待时间 = 长度 / 速度 + (#站数 - 1) * (令牌持有时间) 长度 / 速度 + (#站数) * (令牌持有时间) = 28 至 30 37) 假设 TCP 连接的拥塞窗口大小在超时时为 32 KB。连接的往返时间为 100 毫秒,使用的最大段大小为 2 KB。TCP 连接恢复到 32 KB 拥塞窗口所需的时间(以毫秒为单位)是 . . . . . . . . . . ..
答案:a 说明 当前拥塞窗口大小(按段数计算)=(字节大小)/(最大段大小)= 32KB / 2KB = 16 MSS 在 TCP 的慢启动算法中发生超时时,阈值 减半至 16KB 或 8MSS。并且,慢启动阶段开始 其中拥塞窗口加倍。 因此,从 1MSS 到 8 MSS,窗口大小将呈指数增长。 一个 RTT 后拥塞窗口变为 2MSS,经过 2 个 RTT 后变为 4MSS,经过 3 个 RTT 后变为 8MSS。在 8MSS 时,达到阈值, 并且开始拥塞避免阶段。在拥塞避免阶段, 窗口线性增加。因此,要覆盖从 8MSS 到 16MSS,需要 8 个 RTT。 总共需要 11 个 RTT(慢启动阶段 3 个,拥塞避免阶段 8 个)。 38) 考虑一个选择性重复滑动窗口协议,它使用 1 KB 的帧大小在 1.5 Mbps 的链路上发送数据,单向延迟为 50 毫秒。要实现 60% 的链路利用率,表示序列号字段所需的最小位数是 . . . . . . . . .
答案:c 说明 传输延迟 = 帧大小/带宽 = (1 * 8 * 1024) / (1.5 * 10^6) = 5.33ms 传播延迟 = 50ms 效率 = 窗口大小 / (1 + 2a) = .6 a = 传播延迟/传输延迟 因此,窗口大小 = 11.856(约) 最小序列号 = 2 * 窗口大小 = 23.712 最小序列号所需的位数 = log2(23.712) 答案是 4.56 => 向上取整(4.56) = 5 39) 考虑由三个事务(由下标表示)在使用数据项 x 上的读写操作引起的以下四个调度,分别表示为 r(x) 和 w(x)。哪个是冲突可串行化的。 
答案:d 解释:在选项 D 中,操作没有交错。选项 D 首先是事务 2 的所有操作,然后是事务 3,最后是事务 1。不可能有冲突,因为它是一个序列为 2 -> 3 -> 1 的串行调度。 40) 考虑以下两个陈述 以下哪个是正确的?
答案:a 说明 S1:具有两个单值属性的每个表都处于 1NF、2NF、3NF 和 BCNF。 关系模式 R 处于 BCNF 当且仅当在每个非平凡函数依赖 X->Y 中,X 是超键。如果我们能证明关系处于 BCNF,那么它默认也处于 1NF、2NF、3NF。 令 R(AB) 为一个双属性关系,那么
因此,可以证明具有两个单值属性的关系处于 BCNF,因此它也处于 1NF、2NF、3NF。 因此 S1 为真。 S2:AB -> C, D -> E, E -> C 是函数依赖集 {AB -> C, D -> E, AB -> E, E -> C} 的最小覆盖。 AB -> C, D -> E, AB -> E, E -> C 是函数依赖集 {AB -> C, D -> E, AB -> E, E -> C} 的最小覆盖。 我们知道最小覆盖是消除函数依赖集中冗余函数依赖和多余属性的过程。 因此,F = {AB -> C, D -> E, AB -> E, E -> C} 的每个依赖都应包含在最小覆盖中。 正如我们所见,AB -> E 未包含在最小覆盖中,因为 {AB}+ = ABC 在给定的覆盖 {AB -> C, D -> E, E -> C} 中。 因此,S2 为假。 41) 操作系统在使用三个资源类型 X、Y 和 Z 管理三个进程 P0、P1 和 P2 的分配时,使用了银行家算法进行死锁避免。下表显示了当前系统状态。其中,Allocation 矩阵显示了分配给每个进程的每种资源类型的当前数量,Max 矩阵显示了每个进程在其执行期间所需的每种资源类型的最大数量。  还有 3 个 X 类型、2 个 Y 类型和 2 个 Z 类型单位可用。系统 REQ1:P0 请求 0 单位 X,0 单位 Y 和 2 单位 Z REQ2:P1 请求 2 单位 X,0 单位 Y 和 0 单位 Z 以下哪个是正确的?
答案:b 解释:这是当前的安全状态。 可用 X=3, Y=2, Z=2  现在,如果允许 REQ1 请求,状态将变为 可用 X=3, Y=2, Z=0  现在,利用当前的可用性,我们可以满足 P1 的需求。状态将变为 可用 X = 6, Y = 4, Z = 0  利用由此产生的可用性,由于缺少 Z 资源,将无法满足 P0 或 P2 的需求。 因此,系统将处于死锁状态。 ⇒ 我们不允许 REQ1。 现在,在给定的安全状态下,如果我们接受 REQ2 可用 X = 1 , Y = 2, Z = 2  利用这种可用性,我们服务 P1(也可以服务 P2)。因此,状态是  利用当前的可用性,我们服务 P2。状态变为  最后,我们服务 P0。状态现在变为  由此获得的状态是安全状态。⇒ REQ2 可以允许。 所以,只能允许 REQ2。 因此,B 是正确选项。 42) 考虑以下需要在一个 CPU 上调度的进程集。所有时间均以毫秒为单位。  使用最短剩余时间优先调度算法,平均进程周转时间(以毫秒为单位)为 . . . . . . .
答案:a 解释:进程的周转时间是进程提交到完成的总时间。最短剩余时间(SRT)调度算法选择剩余完成时间最短的进程进行执行。 解决方案 令进程为 A、C、D 和 E。这些进程将按以下顺序执行。甘特图如下  前 3 秒,A 运行,然后剩余时间 A=3, B=2,C=4,D=6,E=3。现在 B 将有机会运行 2 秒,然后剩余时间。A=3, B=0,C=4,D=6,E=3 现在 A 将有机会运行 3 秒,然后剩余时间。A = 0, B = 0,C=4,D=6,E=3 这样做,您将获得上面的甘特图。 调度表  AT = 到达时间,BT = 突发时间,CT = 完成时间,TAT = 周转时间 我们知道,周转时间是进程提交到完成的总时间。即,周转时间=完成时间-到达时间。即,TAT=CT-AT A 的周转时间 = 8 (8 - 0) B 的周转时间 = 2 (5 - 3) C 的周转时间 = 7 (12 - 5) D 的周转时间 = 14 (21 - 7) E 的周转时间 = 5 (15 -10) 平均周转时间为 (8 + 2 + 7 + 14 + 5) / 5 = 7.2。 答案是 7.2。 替代解释 绘制甘特图后,进程 A、B、C、D 和 E 的完成时间分别为 8、5、12、21 和 15。周转时间 = 完成时间 - 到达时间 43) 假设有 3 个页面框,最初是空的。如果页面引用字符串是 1, 2, 3, 4, 2, 1, 5, 3, 2, 4, 6,使用最佳替换策略产生的缺页次数是 . . . . . . . . . .
答案:c 解释:在最佳页面替换策略中,我们替换将来最长一段时间内不使用的页面。 给定三个页面框。 引用字符串是 1, 2, 3, 4, 2, 1, 5, 3, 2, 4, 6 最初,有三次缺页,条目是 1 2 3 页面 4 引起缺页并替换 3(3 是未来最远的),条目变为 1 2 4 总缺页次数 = 3+1 = 4 页面 2 和 1 不引起任何错误。 5 引起缺页并替换 1,条目变为 5 2 4 总缺页次数 = 4 + 1 = 5 3 引起缺页并替换 5,条目变为 3 2 4 总缺页次数 = 5 + 1 = 6 3、2 和 4 不引起任何缺页。 6 引起缺页。 总缺页次数 = 6 + 1 = 7 44) 以下是一个规范的项目集 S --> L.> R Q --> R. 在输入符号 '<' 时,集合有
答案:d 解释:问题是关于符号 ' < ',它不包含在给定的规范项目集中。因此,它在符号 '<' 上既不是移入-归约冲突也不是归约-归约冲突。 因此D是正确选项。 但是,如果问题是关于符号 ' > ',那么它将是一个移入-归约冲突。 45) 令 L 为一个语言,L' 为其补集。以下哪个不是一种可行可能性?
答案:c 说明 A) 如果 L 本身不是 RE,则这是可能的。那么 L' 也不是 RE。 B) 假设存在一种语言,其图灵机在输入时停止。给定的语言是 RE 但非递归,而其补集不是 RE。 C) 这是不可能的,因为如果我们能为两种语言及其补集编写枚举过程,那么该语言就是递归的。 D) 这是可能的,因为如果 L 是递归的,它在补集下是闭合的。 因此,C 是正确选项。 46) 以下哪个正则表达式代表以下 DFA?  I) 0*1(1+00*1)* II) 0*1*1+11*0*1 III) (0+1)*1
答案:b 说明 I) 0 * 1(1 + 00 * 1) * II) 0 * 1 * 1 + 11 * 0 * 1 III) (0 + 1) * 1 (I) 和 (III) 代表 DFA。 (II) 不代表,因为 DFA 接受像 11011 这样的字符串,但正则表达式不接受。 47) 有 5 个袋子,编号从 1 到 5。给定袋子中的所有硬币重量都相同。有些袋子装有重 10 克的硬币,有些装有重 11 克的硬币。我分别从袋子 1 到 5 中取出 1、2、4、8、16 枚硬币。它们的总重量为 323 克。那么装有 11 克硬币的袋子的标签乘积是 . . . . . . . . .
答案:b 说明 有 5 个编号为 1 到 5 的袋子。 我们不知道有多少袋子装有 10 克和 11 克的硬币。 我们只知道总重量是 323。 现在这里的想法是得到总和的个位数 3。 标记 1 号袋子装有 11 克硬币。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 标记 2 号袋子装有 10 克硬币。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 标记 3 号袋子装有 11 克硬币。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 标记 4 号袋子装有 11 克硬币。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 标记 5 号袋子装有 10 克硬币。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 注意:上述标记是在得到一些不同排列的错误 结果后完成的,这些排列在总和的个位数上产生 3。 现在,我们分别从袋子 1 到 5 中取出了 1、2、4、8、16 枚硬币。 因此,每个袋子从 1 到 5 的总和分别为 11、20、44、88、160 克。 对于上面的组合,我们得到的总和个位数是 3。 让我们找出总和,它是 11 + 20 + 44 + 88 + 160 = 323。 所以它是正确的。 现在装有 11 克硬币的袋子是 1、3 和 4。 因此,乘积是:1 x 3 x 4 = 12。 替代解决方案 有装有 11 克和 10 克硬币的袋子。从袋子 1、2、3、4、5 中取出的 1、2、4、8、16 枚硬币的总重量为 323 克。 现在我们需要找出多少枚 10 克和 11 克的硬币可以得到 323 克的总和。 设 x 为 10 克硬币的数量,y 为 11 克硬币的数量 因此 10x + 11y = 323. . . . . . . . . . . . . .1 现在我们知道取出的总硬币数量,即 1+2+4+8+16=31。 因此 x + y = 31. . . . . . . . . . . . . . . . .2 求解方程 1 和 2 得到 x=18, y=13。 因此袋子 2 和 5(2+16=x=18)装有 10 克硬币,袋子 1、3 和 4(1+4+8=y=13)装有 11 克硬币。 因此,装有 11 克硬币的袋子的标签乘积是 1 x 3 x 4 = 12。 48) 假设发现了一个多项式时间算法,可以正确计算给定图中的最大团。在这种情况下,以下哪个代表复杂度类 P、NP 和 NP 完全(NPC)的正确维恩图? 
答案:d 解释:团是一个 NP 完全问题。如果一个 NP 完全问题可以在多项式时间内解决,那么所有 NP 完全问题都可以。因此 NPC 集等于 P。 49) 找到 100 个数字的最小值和最大值所需的最小比较次数是 . . . . . . . . . .
答案:a 说明 查找 n 个数字的最小和最大元素的步骤
因此,对于每 2 个元素,我们需要 3 次比较,所以所需的总比较次数为 (3n)/2 - 2,因为在第一步中我们不需要更新 min 或 max。 递推关系为 T(n) = T(⌈n/2⌉)+T(⌊n/2⌋)+2 = 2T(n/2)+2 = ⌈3n/2⌉-2 将值 n=100 代入,(3*100/2)-2 = 148,这就是答案。 50) 考虑以下 C 函数,其中 size 是数组 E 中的元素数量。 函数 MyX 返回的值是
答案:a 说明 函数执行以下操作 Y 用于存储迄今为止看到的最大总和,Z 用于存储当前总和 1) 初始化 Y 为所有元素的总和 2) 对于每个元素,计算以 arr[i] 开头的所有子数组的总和。将当前总和存储在 Z 中。如果 Z 大于 Y,则更新 Y。 51) 考虑以下伪代码。需要执行的总乘法次数是多少?
答案:c 说明 语句“D = D * 3”被执行 n*(n+1)*(n-1)/6 次。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 让我们看看如何。 对于 i = 1,乘法语句执行 (n-1) + (n-2) + . . . . . . 2 + 1 次。 对于 i = 2,语句执行 (n-2) + (n-3) + . . . . . . . . . . . 2 + 1 次 对于 i = n-1,语句执行一次。 对于 i = n,语句不执行。 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 因此,总的来说,该语句被执行的次数如下 [(n-1) + (n-2) + . . . . . . . . . . . 2 + 1] + [(n-2) + (n-3) + . . . . . . . . . . . 2 + 1] + . . . . . . . . . . . .+ 1 + 0 上述级数可以写成 S = [n*(n-1)/2 + (n-1)*(n-2)/2 +. . . . . . . . . . . + 1] 可以通过从标准级数 S1 = n2 + (n-1)2 + . . . . . . . . . . 12 中减去该级数来获得该级数的总和。该标准级数的总和为 n*(n+1)*(2n+1)/6。 S1 - 2S = n + (n-1) + . . . . . . . . . . 1 = n*(n+1)/2 2S = n*(n+1)*(2n+1)/6 - n*(n+1)/2 S = n*(n+1)*(n-1)/6 上述解决方案 依赖于一个技巧来获得级数的总和,但有一个更直接的方法可以获得相同的结果。 对于 i = 1,乘法语句执行 (n-1) + (n-2) + .. 2 + 1 次。 对于 i = 2,语句执行 (n-2) + (n-3) + . . . . . . . . . ..2 + 1 次 因此,对于每个 i,语句执行的次数为  这是从 1 到 n - i 的 n 个自然数的总和。因此,它可以简化为  - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 相乘,我们将得到以下结果  现在,这是语句将执行的次数。因此,总共执行该语句的次数为  - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 暂时忽略一半。展开求和很简单。您可以将其分配到表达式中以获得  - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 使用 n 个自然数求和以及 n 个自然数平方求和的公式,我们得到  - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 进一步简化并取 n/6 作为公项将得到  现在,取 2 作为公项,并用它来抵消之前忽略的一半。这给你  最后,使用 a^2-b^2,你得到所需答案  这应该使解决方案对您来说更清晰! 52) 考虑一个有 9 个槽的哈希表。哈希函数为 ?(k) = k mod 9。通过链表解决冲突。按顺序插入以下 9 个键:5、28、19、15、20、33、12、17、10。哈希表中的最大、最小和平均链长度分别为
答案:a 说明 以下是所有键的哈希函数值 5 --> 5 28 --> 1 19 --> 1 [与 28 链接] 15 --> 6 20 --> 2 33 --> 6 [与 15 链接] 12 --> 3 17 --> 8 10 --> 1 [与 28 和 19 链接] 最大链长度为 3。键 28、19 53) 考虑一个 6 阶段的指令流水线,其中所有阶段都完美平衡。假设流水线没有周期时间开销。当应用程序在这个 6 阶段流水线上执行时,与非流水线执行相比,如果 25% 的指令产生 2 个流水线停顿周期,则实现的加速比是
答案:a 说明 这是一个数字类型的题目,所以答案必须是 4。 对于 6 个阶段,非流水线需要 6 个周期。 25% 的指令有两个停顿周期 所以流水线时间 = (1 + (25 / 100) * 2) = 1.5 加速比 = 非流水线时间 / 流水线时间 = 6 / 1.5 = 4 54) 缓存块地址的访问序列长度为 N,包含 n 个唯一的块地址。在相同块地址的两次连续访问之间,唯一块地址的数量上限为 k。如果访问序列通过关联度 A >=k 的缓存,并执行最近最少使用替换策略,那么命中率是
答案:a 说明 有 N 次缓存块访问请求,其中 n 个块是唯一的。在同一个块的两次访问之间,有 (k-1) 其他块的请求。如果它们的关联度 >=k 并且使用 LRU,那么对于每个唯一块,即 n,只会发生一次缓存未命中,即当它们第一次进入缓存时。因此,未命中率 =(缓存未命中)/(请求数)= n / N 55) 考虑一个 4 对 1 的多路复用器,具有两条选择线 S1 和 S0,如下所示 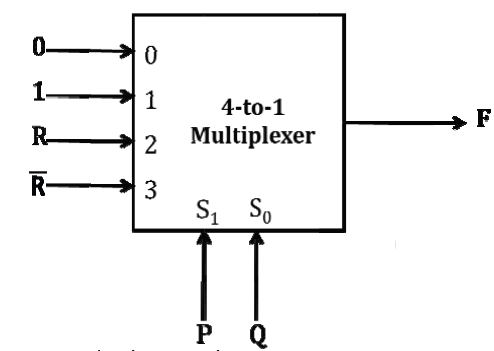 多路复用器的输出 F 的最小积之和形式是
答案:a 说明 对于 4 对 1 的多路复用器 =p'q'(0)+p'q(1)+pq'r+pqr' =p'q+pq'r+pqr' =q(p'+pr')+pq'r =q(p'+r')+pq'r =p'q+qr'+pq'r 答案 (a) 56) 函数 f(x) = x sinx 满足以下方程 f"(x) + f(x) + t cosx = 0。t 的值是
答案:b 说明 我们有 f(x) = x sin x ⇒ f'(x) = x cos x + sin x ⇒ f′′(x) = x (− sin x ) + cos x + cos x = (−x sin x ) + 2 cos x 现在,给定 f(x)=x sin x 满足方程 f′′(x) + f(x) + t cos x = 0 ⇒ (−x sin x ) + 2 cos x + x sin x + t cos x = 0 ⇒ 2 cos x + t cos x = 0 ⇒ cos x ( t + 2 ) = 0 ⇒ t + 2 = 0 ⇒ t = −2 因此,B 是正确选项。 57) 一个函数在区间 [0, 2] 上是连续的。已知 f(0) = f(2) = -1 且 f(1) = 1。以下哪个陈述必须为真 . . . . . . . . .?
答案:a 说明  由于函数是连续的,在 0 和 1 之间必须有一个点,它变为 0,并且在 1 和 2 之间也必须有一个点,它变为 0。 58) 掷四颗公平的六面骰子。总和为 22 的概率为 X/1296。X 的值是 . . . . . . . . . . . . .
答案:d 说明 一般来说,概率(事件)=有利结果数/随机实验中的总可能结果数。 这里,掷 4 个六面骰子,对于一个骰子可以有 6 个等可能且互斥的结果。 将 4 个骰子一起考虑,总共有 6*6*6*6 = 1296 种可能的结果。 现在,事件的有利情况数:这里事件是总和为 22。 因此,只有 2 种可能的情况。 情况 1:三个 6 和一个 4,例如:6,6,6,4(总和为 22) 因此,获得此结果的方法数 = 4!/3! = 4 种方法(3! 用于消除所有三个 6 相互交换的情况) - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 情况 2:两个 6 和两个 5,例如:6,6,5,5(总和为 22) 因此,获得此结果的方法数 = 4!/( 2! * 2!) = 6 种方法(2! 用于消除两个 6 相互交换的情况,对两个 5 也一样) 因此,有利情况的总数 = 4 + 6 = 10。 因此概率 = 10/1296。 因此选项 D。 59) 旗帜是数字序列,每个数字是 1 或 2。n-旗帜是总和等于 n 的数字序列。例如,(1,1,2) 是一个 4-旗帜。所有可能的 1-旗帜的集合是 {(1)},所有可能的 2-旗帜的集合是 {(2), (1,1)},所有 3-旗帜的集合是 {(2,1), (1,1,1), (1,2)}。请注意,旗帜 (1,2) 与旗帜 (2,1) 不同。10- 旗帜的数量是 - - - - - - - - - - - - -
答案:a 说明 1 - 旗帜 {(1)} - - - - - - - - - - - - - -- - - - - #1 2 - 旗帜 {(1, 1), (2)} - - - - - - - - - - - - - - -#2 3 - 旗帜 {(1, 1, 1), (1, 2), (2, 1)} - - - - - - - - - - - #3 4 - 旗帜 {(1, 1, 1, 1), (2, 2), (1, 1, 2), (1, 2, 1), (2, 1, 1)} - - - - - - - - - - - - - #5 5 - 旗帜 {(1, 1, 1, 1, 1), (2, 1, 1, 1), (1, 2, 1, 1), (1, 1, 2, 1 ), (1, 1, 1, 2), (2, 2, 1), (2, 1, 2),(1, 2, 2)} - - - - - - - - - - - - - --#8 如果仔细观察,它们是斐波那契数列的项(一部分)。(0, 1, 1, 2, 3, 5, 8, 13 . . . . . . . . . . . . . 因此,10-旗帜的数量是该数列的第 12 项,即 89。 60) 令 S 为所有函数 f: {0,1}4 -> {0,1} 的集合。令 N 为 S 到集合 {0,1} 的函数数量。Log2Log2N 的值是 . . . . . . . . . . . . . .
答案:d 说明 给定的映射 S 定义为 f:{0,1}^4 -> {0,1}。 所以,S 的函数数量将是 2^16。 现在 N 定义为 f: S-> {0,1}。 所以,S 到 {0,1} 的函数数量将是 2^S。 因此 log2log2N = log2S = 16 61) 考虑一个无自环的无向图 G。G 的顶点集为 {(i,j): 1 <= i<= 12, 1 <= j <= 12}。当 |a - c| <= 1 且 |b - d| <= 1 时,顶点 (a, b) 和 (c, d) 之间存在一条边。 图中边的数量是。 . . . . . . . . . . . . . . . . .
答案:c 说明 给定 G 的顶点集为 {(i, j): 1 <= i<= 12, 1 <= j <= 12}。 当 |a - c| <= 1 且 |b - d| <= 1 时,顶点 (a, b) 和 (c, d) 之间存在一条边。 总共有 12*12 = 144 个可能的顶点。这些顶点是 (1, 1), (1, 2) . . . .. . . .(1, 12) (2, 1), (2, 2), . . . . . . . . . . . 图中边的数量是多少? 边的数量等于满足上述条件的顶点对的数量。例如,顶点对 {(1, 1), (1, 2)} 满足上述条件。 对于顶点 (1, 1),它可以连接到 (1, 2), (2, 1), (2, 2)。请注意,正如问题中所述,可能存在自环。 对于 (12, 12), (1, 12) 和 (12, 1) 的计数相同。 对于顶点 (1, 2),它可以连接到 (1, 1), (2, 1), (2, 2), (2, 3), (1, 3)。 对于 (1, 3), (1, 4). . . . . . . . . . .(1, 11), (12, 2), . . . . . . . . . . .(12, 11) 的计数相同。 对于顶点 (2, 2),它可以连接到 (1, 1), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2), (3, 3)。 对于剩余的顶点,计数相同。 对于所有顶点 (i, j),如果 i 和 j 不在 {1, 12} 中,则总共有 8 个顶点与它们相连。 总共有 100 个不包含 1 或 12 的顶点。所以总共有 800 条边。 对于包含 1 的顶点,总边数 = (1 作为第一部分的边的数量) + (1 作为第二部分但不是第一部分的边的数量) = (3 + 5 * 10 + 3) + (5 * 10) 条边 对于包含 12 的顶点的计数相同。 总边的数量 = 800 + [(3 + 5 * 10 + 3) + 5 * 10] + [(3 + 5 * 10 + 3) + 5 * 10] = 800 + 106 + 106 = 1012 由于图是无向的,从 v1 到 v2 和从 v2 到 v1 的两条边 应被计为一条。 因此,无向边的总数为 1012 / 2 = 506。 62) 一个有序 n-元组 (d1, d2,. . . . . , dn) 满足 d1 >= d2 >=. . . . . . . . .>= dn,如果存在一个具有 n 个顶点且度数分别为 d1, d2, . . . . . . . ., dn 的简单无向图,则称该 n-元组是图的。以下哪个 6-元组不是图的?
答案:c 解释: 使用 (3, 3, 3, 1, 0, 0) 的度数集合,无法构成所需的图。使用这个 6-元组,形成的图将是一个不连通的无向图,其中图的两个顶点不应连接到图中的任何其他顶点(即,两个顶点的度都为 0)。对于剩余的 4 个顶点,图需要满足 (3, 3, 3, 1) 的度数。 让我们通过图的逻辑结构来理解这一点。 假设顶点标记的度数分别为 <3, 3, 3, 1, 0, 0>。  现在 E 和 F 不应与图中的任何顶点相连。A、B、C 和 D 的度数应分别为 <3, 3, 3, 1>。现在,为了满足 A、B 和 C 的要求,节点 D 将永远无法达到其度为 1 的要求。它的度数也将变为 3。这在上面的图中显示了出来。 因此,元组 <3, 3, 3, 1, 0, 0> 不是图的。 63) 当 p, q, r 中恰好有两个为 TRUE 时,以下哪个命题逻辑公式为 TRUE? 
答案:b 解释: 画出三个变量的真值表,只有当恰好有两个变量为 1 (true) 时输出才为 1 (true),否则输出为 0 (false)。 因此, p q r Output (f) - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 0 f = ( ~p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) ∨ (p ∧ q ∧ ~r) f = {( ~p ∧ q ) ∨ (p ∧ ~q )} ∧ r ∨ (p ∧ q ∧ ~r) f = {(p ⊕ q )} ∧ r ∨ (p ∧ q ∧ ~r) f = {~ (p ↔ q )} ∧ r ∨ (p ∧ q ∧ ~r) 因此,选项 (b) 是正确的。 64) 给定以下模式 employees(emp-id, first-name, last-name, hire-date, dept-id, salary) departments(dept-id, dept-name, manager-id, location-id) 您想显示位于 location ID 1700 的各个部门的最新入职员工的姓氏和入职日期。您执行了以下查询 结果是什么?
答案:b 解释: 给定的查询使用了下面的内部查询。 SELECT dept-id, MAX(hire-date)FROM employees JOIN departments USING(dept-id)WHERE location-id = 1700GROUP BY dept-id 内部查询在 location id 为 1700 的每个部门中生成最新的入职日期。 外部查询仅选择内部查询的所有对。因此,查询产生正确的结果。 SELECT last-name, hire-date FROM employeesWHERE (dept-id, hire-date) IN(Inner-Query); 65) 考虑两个处理器 P1 和 P2,它们执行相同的指令集。假设在相同条件下,对于相同的输入,在 P2 上运行的程序所需时间比在 P1 上运行的程序少 25%,但 CPI(每条指令的时钟周期数)却高 20%。如果 P1 的时钟频率为 1GHz,那么 P2 的时钟频率(以 GHz 为单位)是 . . . . . . . . . . . . . ..
答案:a 说明 对于 P1,时钟周期 = 1ns 令 P2 的时钟周期为 t。 现在根据规格考虑以下方程 7.5 ns = 12*t ns 我们得到 t,t 的倒数将是 1.6GHz。 下一主题GATE 2013 |
我们请求您订阅我们的新闻通讯以获取最新更新。