Python统计模块

统计学是一种收集数据、将其整理成表格形式并解释数据以得出结论的方法。它是应用数学的一个领域，涉及数据的收集、分析和解释。利用统计学，我们可以分析和解释复杂问题中的复杂数据。在本文中，我们将探讨如何使用 Python 解决统计问题，还将介绍 Python 提供的统计模块。

Python 的 statistics 模块提供了各种函数来解决和查找数值数据的统计量。该模块提供了各种函数，例如 mean()、Median()、mode()、standard deviation() 等。

在统计模块中，我们通常使用描述性统计，例如均值，并通过某种表示方法（如表格、图表或 Excel 文件）来描述数据。数据以突出某些有意义的见解以发现未来趋势的方式进行表示。用单个变量描述和总结数据称为单变量分析。当我们发现两个变量之间的关系时，称为双变量分析。如果包含两个以上的变量，则称为多变量分析。

描述性统计方法

描述性统计可以通过两种方法进行评估，这两种方法可用于根据特定目的解释数据。

1. 集中趋势度量
2. 离散度度量

集中趋势度量

集中趋势度量指的是一个描述整个数据的单一数值。集中趋势度量有三种类型。

• 平均数
• 中位数
• 众数

平均数

它提供了数据中观测值之和的平均值。

均值的公式是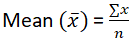

在 Python 中，mean() 函数提供作为参数传递的数据的均值。如果我们不向 mean() 函数传递任何数据，则会引发一个名为 StatisticsError 的错误。

输出

The mean of data is: 3

说明

在上面的代码中，我们将 statistics 模块导入为 st，将数据列表 input 作为 data，并使用 statistics 模块提供的 mean() 函数打印数据的均值。

中位数

中位数表示数据的中间值。它将数据分为两半。如果数据中的值数量是奇数，则中心值就是中位数；如果是偶数，则在这种情况下，中位数是两个中心值的均值。

要查找中位数，我们首先对数据进行排序，然后查找数据的中位数。在 Python 中，如果你不向 median() 函数提供任何数据，则会引发 StatisticsError。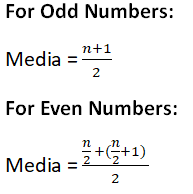

输出

Median of scores1 is 20
Median of scores2 is 8.9
Median of scores3 is 5/6
Median of scores4 is -13
Median of scores5 is 2.5

说明

在上面的代码中，我们首先使用元组创建各种分数，然后使用 Median() 方法查找分数的 Median。

Median Low

median_low() 方法在数据元素数量为奇数时提供中位数，但如果数据中的值数量为奇数，则它提供两个中间值中较小的那个。这是演示 statistics 模块提供的 median_low() 函数的 Python 代码。

输出

Median of ages is 23.5
Low Median of ages is 23

说明

上面的代码提供了年龄的中位数，数据中的值的数量是偶数；Median() 函数提供了两个中间值的均值；另一方面，median_low_() 函数提供了两个中间值中较小的那个。

Median High

如果数据中的值数量是奇数，median_high() 函数就提供数据的中位数，但如果数据中的值数量是偶数，则它提供两个中间值中较大的那个。这是 median_high 函数的 Python 代码。

输出

Median of weights is 61.0
The High Median of weights is 62

说明

在上面的代码中，我们使用 Median() 函数查找权重的 Median，它提供了中间值，而 median_high() 函数返回两个中间值中较大的那个。

众数

众数也用作集中趋势度量，它提供了数据中出现频率最高的值。如果数据中所有值的计数都相同，则数据可能不提供任何众数。如果数据中的两个或多个值具有相同的计数，则我们可以得到多个众数。在 Python 统计模块中，mode() 函数提供了数据值中的最大计数。众数可用于分类数据和数值数据。

输出

Mode of scores_a is 8
Mode of scores_b is 3.2
Mode of scores_c is 3/5
Mode of scores_d is -10
Mode of scores_e is apple

说明

在上面的代码中，我们使用元组创建了五个分数，包括数值、浮点、整数和分类数据。然后，我们使用 statistics 模块提供的 mode() 函数查找每个分数的众数。

离散度度量

仅仅衡量数据的集中趋势不足以提供数据的描述。还需要离散度度量来描述数据，也称为数据的散布，表示数据是如何散布的。离散度度量有各种类型。

• 范围
• 变化
• 标准差

范围

极差是数据中最大值和最小值之间的差值。它与数据的散布成正比，这意味着数据的散布越大，极差也越大。

极差的公式是

极差 = 最大值 - 最小值

可以使用 max() 和 min() 函数计算最大值和最小值。

输出

Maximum = 33, Minimum = 10 and Range = 23

说明

在上面的代码中，创建了一个值列表，使用函数计算了最大值和最小值，并使用极差公式计算了数据的散布。

变化

方差是偏差的平方与均值之间差值的均值。要找到方差，我们首先找到每个点与均值之间的差值，将其平方并相加，然后除以数据中存在的总数据值。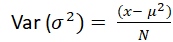

其中 N 是数据中的值数量，μ 是均值。

输出

Variance of group1 is 7.238095238095238 
Variance of group2 is 7.866666666666666 
Variance of group3 is 49.410714285714285 
Variance of group4 is 2/5 
Variance of group5 is 0.385 

说明

在上面的代码中，我们首先从 statistics 模块导入 variance 函数，创建五个数据组，然后计算数据的方差。

标准偏差

它是通过方差的平方根计算的。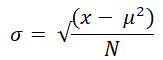

在 Python 中，statistics 模块提供了 stdev() 函数，该函数提供数据的标准差。

输出

The Standard Deviation of scores1 is 2.563479777846623
The Standard Deviation of scores2 is 2.3166067138525404
The Standard Deviation of scores3 is 6.468329437674438
The Standard Deviation of scores4 is 0.9354143466934856

说明

stdev 函数从 statistics 模块导入，使用元组创建了五个数据分数，并计算了每个分数的标准差。

调和平均数

调和平均数是通过算术平均数的倒数计算的。例如，三个点 x、y 和 z 的调和平均数将评估为 3/(1/x + 1/y + 1/z)。如果任何点的值为零，则结果为零。

输出

Harmonic mean of numbers1 is 18.604651162790695
Harmonic mean of numbers2 is 3.9887064558944534

几何平均数

几何平均数也是一种集中趋势度量，通过值的乘积计算，这与使用总和的算术平均数相反。

输出

Geometric mean of data1 is 10.95445115010332
Geometric mean of data2 is 3.443485356947653

核密度估计 (KDE)

离散数据的 KDE 使用核函数通过平滑数据提供连续概率分布，用于从数据样本中得出关于总体的结论。缩放参数 'h' 控制平滑度，称为带宽。小值会促进局部特征；另一方面，大值会提供平滑的结果。

KDE 中的核函数会评估样本数据值的相对权重。选择核函数的形状并不重要，因为它对平滑参数影响不大。

输出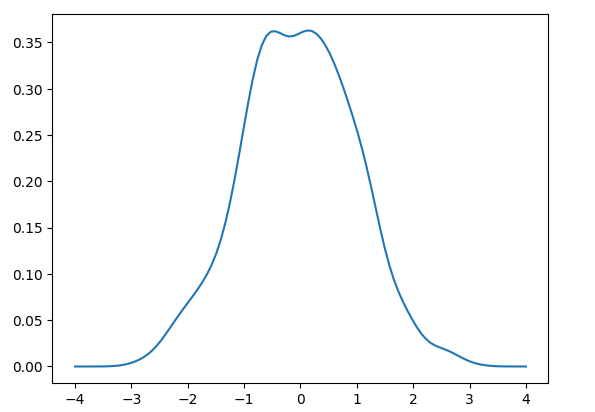

说明

在上面的代码中，导入了 scipy 模块以查找给定数据集的 KDE。

分位数

此函数将数据分成 n 个具有相等概率的连续区间。如果我们设 n 的值为 4，那么它会找到四分位数；如果 n 的值是，那么它返回十分位数；如果 n 的值为 100，那么它给出百分位数。在该函数中，我们传入了任何可迭代样本值的数据。

输出

Quartiles: [26.5, 39.0, 49.0]
Deciles: [19.2, 23.4, 29.4, 32.2, 39.0, 41.2, 46.2, 51.4, 54.2]
25th Percentile: 26.5
50th Percentile (Median): 39.0
75th Percentile: 49.0

说明

在上面的代码中，n 是分组的数量，例如四分位数为 4，十分位数为 10，百分位数为 100。

协方差

此函数提供两个输入值 a 和 b 之间的协方差。它评估两个输入值的联合变异性。

输出

Covariance between x and y: 69.2

相关性

Python statistics 模块提供的 correlation 函数返回两个输入值的皮尔逊相关系数。相关系数的值在 -1 和 +1 之间。它提供了线性关系的方向和强度。如果相关系数的值为 -1，则称为负相关；如果其值为 +1，则称为正相关。如果其值为 0，则表示没有相关性。

输出

Correlation between x and y: 0.9947213949442446

说明

在上面的代码中，我们取了两个输入变量 x 和 y，并使用 statistics 模块计算了这些变量之间的皮尔逊相关系数。