Python中的Tim排序

Python 中的 Tim Sort 是一种混合排序技术，它融合了插入排序和归并排序的优点和效率。

Python 中的 Tim Sort 方法将数组分成多个称为“Runs”的子数组，这些子数组已经是排序好的。通过合并所有较小的已排序 Runs 中的元素，最终得到一个完全排序的数组。

Tim Sort 是如何工作的？

让我们通过一个例子来深入了解 Tim Sort。

我们将以数组 arr[] = {18, 2, 1, 12, 5, 3, 8, 11, 7} 为例，并分五个步骤来理解它。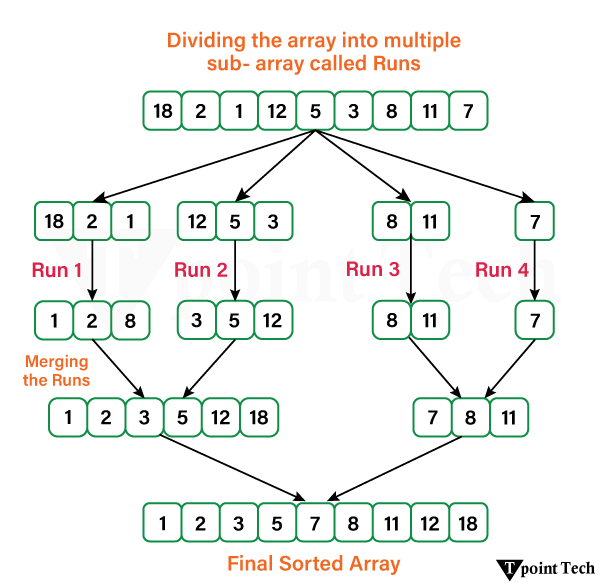

步骤 1：定义 Run 的大小

• 在这里，定义了 Run 的大小。
• 最小 Run 大小：32（这个最小大小在这里不重要，因为数组很小）

步骤 2：识别 Runs

将数组分成多个称为 Runs 的子数组。让我们逐步查看这些 Runs。

• Run 1 = 降序子数组 [18, 2, 1] 被 Tim Sort 反转为 [1, 2, 18]。
• Run 2 = [12, 5, 3] 也是降序的，所以 Tim 会将其反转为 [3, 5, 12]。
• Run 3 = [8, 11] 已经按升序排列，因此将保持不变。
• Run 4 = [7] 是一个单元素 Run，保持原样。

步骤 3：合并 Runs

在此步骤中，我们将使用修改后的 归并排序 方法来合并所有 Runs。通过合并所有 Runs，整个数组将被排序。

• 合并 [1, 2, 18] 和 [3, 5, 12]，结果为 à [1, 2, 3, 5, 12, 18]
• 合并 [8, 11] 和 [7] 得到 [7, 8, 11]
• 现在我们将进行最终合并：[1, 2, 3, 5, 12, 18] + [7, 8, 11] à [1, 2, 3, 5, 7, 8, 11, 12, 18]。
• 最终排序的数组是：[1, 2, 3, 5, 7, 8, 11, 12, 18]

步骤 4：调整 Run 的大小

• 我们需要在每次合并操作后将 Run 的大小加倍。
• 由于数组很小，这里不需要这样做。

步骤 5：继续合并

• 合并过程将重复进行，直到整个数组被排序。
• 最终合并的 Run：[1, 2, 3, 5, 7, 8, 11, 12, 18]
• 因此，我们得到了最终排序的数组：[1, 2, 3, 5, 7, 8, 11, 12, 18]

Tim Sort 的伪代码

让我们看看 Python 中 Tim Sort 的伪代码，以更好地理解这个主题。Python

说明

在上面的伪代码中，我们将最小 Run 大小定义为 32。我们使用 calcMinRun() 函数来计算数组的最小 Run 大小。之后，我们使用插入排序对小的 Runs 进行排序，然后合并这些排序后的子数组，直到整个数组被排序。

Python 中 Tim Sort 的实现

在下面的示例中，我们将看到 Python 中 Tim Sort 的实现。

输出

Given Array is
[18, 2, 1, 12, 5, 3, 8, 11, 7]
After Sorting the Array is
[1, 2, 3, 5, 7, 8, 11, 12, 18]

说明

在上面的代码中，我们将最小 Run 大小定义为32。然后，我们使用 calcMinRun() 函数为给定的数组计算最佳最小 Run 大小。之后，我们将数组分成小的 Runs 并使用插入排序方法对它们进行排序。最后，使用merge函数迭代地合并这些排序后的子数组，直到整个数组被排序。

Python 中 Tim Sort 的复杂度分析

Python 中的 Tim Sort 包括时间复杂度和空间复杂度。

时间复杂度

最佳情况时间复杂度

当数组已排序或几乎排序时，称为最佳情况时间复杂度，此时最佳情况复杂度为 O(n)。

平均情况时间复杂度

当数组中的元素是随机排列的时，会出现平均情况时间复杂度。Python 中 Tim Sort 的平均情况时间复杂度为O(n log n)。

空间复杂度：Tim Sort 的空间复杂度为O(n)，因为它在合并时需要额外的内存。

结论

Tim Sort 由两种排序方法组成：归并排序和插入排序。它将数组分成多个称为 Runs 的子数组，这些子数组已经排序。之后，通过一个遍历数组的算法将元素收集起来并合并成一个单一的排序列表。我们学习了复杂度分析，包括时间复杂度和空间复杂度。

常见问题解答 (FAQs)

1. Python 中的 Tim Sort 是什么？

Python 中的 Tim Sort 是一种混合排序技术，它融合了插入排序和归并排序的优点和效率。

2. Python 中的 Tim Sort 有什么含义？

Python 中的 Tim Sort 方法以 Tim Peters 的名字命名，他于 2002 年为 CPython 实现设计了它。

3. Python 中 Tim Sort 的时间复杂度是多少？

Tim Sort 中存在最佳情况和平均情况的 Tim 复杂度。最佳情况时间复杂度为 O(n)，平均情况时间复杂度为 O(n log n)。

4. Tim Sort 中是否存在最坏情况时间复杂度？

我们可以考虑最坏情况复杂度。TimSort 的最坏情况是 O(n log n)，这对于性能保证很重要。

5. Python 中的 Tim Sort 中“Runs”是什么？

Python 中的 Tim Sort 方法将数组分成多个称为 Runs 的子数组，这些子数组已经是排序好的。Tim Sort 使用这些 Runs 来合并它们。

6. Python 中的 Tim Sort 是如何工作的？

Python 中的 Tim Sort 方法将数组分成多个称为 Runs 的子数组，这些子数组已经是排序好的。通过合并子数组，就完成了完全排序的数组，就像在归并排序中一样。