数据挖掘中的属性选择度量

在本文中，我们将理解数据挖掘中的属性选择度量。

属性选择也称为变量选择或特征选择。它在数据挖掘中非常重要，因为它有助于构建决策树。属性、变量或特征是数据的方面。假设数据集中存在不相关的信息或数据中的噪声，这会负面影响数据挖掘模型的性能。在这种情况下，在训练阶段发现信息将变得困难。属性选择是删除训练数据集中不相关和冗余属性的过程。属性选择旨在提高数据挖掘模型的性能并减少过拟合，从而使模型更易于理解。

属性选择是一种启发式方法，用于选择最佳的划分标准，以将给定的类标记的训练元组的“D”分区划分为各个类。它选择根节点和子节点的最优属性。它指定如何划分给定节点处的元组。它为描述给定训练元组的每个属性提供一个排名。有各种属性选择度量，我们可以借助它们选择相关的属性，如下所示：

熵

该概念用于查找给定数据集中存在的混乱度。简单来说，我们可以说熵告诉我们数据集中存在的杂质。它决定了划分数据的最佳分割点。

以下是熵的数学公式

在上式中，

• Entropy (D) 是数据集“D”的熵。
• “n”是数据集中不同类或类别的数量。
• “p_i”是类别 i 中的数据点数与“D”中数据点总数的比例。

为了计算数据集的熵，公式将属于每个不同类别或类别的所有数据点比例相加。负号用于确保熵为正值。此公式通常使用以 2 为底的对数（2log₂），使熵的单位为比特。

注意：如果熵很高，则数据集的类别标签更加异构。如果熵低，则表示数据集是同质的。

信息增益 (Information Gain)

它用于查找基于属性划分数据集后熵的变化。它用于告诉我们一个属性可以为我们提供多少关于类别的信息。我们选择导致熵最大化减少的特征，因为它提供了更多信息。

信息增益可以通过以下公式计算

Information Gain (IG) = Entropy (D) - [(Weighted average)*Entropy (each Feature)
OR
IG (D, A) = H(D) - ∑ (|Dv|/|D|)⋅H(Dv)

在上式中，

• “IG (D)”是基于属性 A 的数据集“D”的信息增益。
• “H (D)”是数据集“D”的熵。
• “|D_v|”是子集 v 中的实例数。
• “|D|”是数据集“D”中的实例总数。
• “H(D_v)”是每个子集 v 的熵。

注意：具有最高信息增益的特征被选为当前节点的分割特征，以首先进行分割。

基尼指数

它也称为基尼系数、基尼杂质或基尼比率。它用于查找数据集中的杂质。它找出树内所有分割的概率。它有助于决定在构建决策树时如何分割数据集。基尼指数的值介于 0 和 1 之间。

注意：如果基尼指数值为 0，则表示数据集是纯净的，或者所有数据点都属于同一类别。如果基尼指数值为 1，则表示数据集是不纯净的，或者数据点属于多个类别。如果基尼指数值为 0.5，则表示数据集中数据点的分布在多个类别之间是均匀的，数据集是不纯净的。

在决策树中，每个节点都是一个包含信息的属性。我们将计算每个节点上的基尼指数，基尼指数最低的地方将作为树的分割标准。

计算基尼指数的数学公式如下

在上式中，

• Gini (D) 是数据集“D”的基尼指数。
• P_i 是数据集中属于第 i 个类别的数据点的概率。

计算基尼指数、信息增益和熵的示例

以下是训练数据集“D”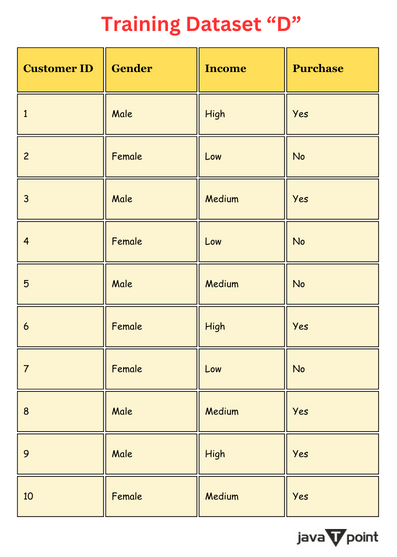

计算数据集“D”的熵

让我们计算上述数据集的熵

Entropy (D) = -p₁log₂(p₁) - p₂log₂(p₂)，其中 p₁ 和 p₂ 是数据集中“是”和“否”的比例。

对于数据集“D”，p₁ = 6/10，p₂ = 4/10

Entropy (D) = -(6/10) log₂ (6/10) - (6/10) log₂ (4/10) = 0.971

上述数据集“D”的熵为 0.971。

计算数据集“D”的信息增益

我们将计算数据集“D”对于“性别”特征的信息增益（IG）。

为此，我们首先需要计算“性别”特征的熵。

对于“男性”

|D_Male| = 5

Entropy (D_Male) = - i=1∑n pi⋅log2(pi)

Entropy (D_Male) = - (3\5) log₂ (3\5) -(2\5) log₂ (2\5)

对于“女性”

|D_Female| = 5

Entropy (D_Female) = - i=1∑n pi⋅log2(pi)

Entropy (D_Female) = -(3\5) log₂ (3\5) -(2\5) log₂ (2\5)

现在，我们将计算信息增益。

IG (D, Gender) = Entropy (D) - (5/10)Entropy (D_Male) - (5/10)Entropy (D_Female)

我们将把 Entropy (D)、Entropy (D_Male) 和 Entropy (D_Female) 的值代入上面的 IG (D, Gender) 表达式。

IG (D, Gender) = Entropy (D) - (5/10)[-(3\5) log₂ (3\5) - (2\5) log₂ (2\5)] - (5/10) [-(3\5) log₂ (3\5) -(2\5) log₂ (2\5)]

IG (D, Gender) = 0.971 + (3\10) log₂ (3\5) + (2\10) log₂ (2\5) + (3\10) log₂ (3\5) + (2\10) log₂ (2\5)

IG (D, Gender) = 0.971+(103)⋅(-0.737)+(102)⋅(-1.322)+(103)⋅(-0.737)+(102)⋅(-1.322)

IG (D, Gender) = 0.971-0.2211-0.2644-0.2211-0.2644

IG (D, Gender) ≈ 0.000

上述数据集“D”的信息增益（IG）为 0.000。

计算数据集“D”的基尼指数

我们将计算数据集“D”的基尼指数。

Gini = 1 - n∑i=1 (pi)²

p₁ 和 p₂ 是数据集中“是”和“否”的两个比例。

p₁ = 6/10;

p₂ = 4/10

Gini (D) = 1 - [(6/10)² + (4/10)²]

Gini (D) = 1 - (36/100) - (16/100)

Gini (D) = 1 - (13/25)

Gini (D) = 12/25

Gini (D) ≈ 0.480

上述数据集“D”的基尼指数为 0.480。

我们已经计算了给定数据集“D”的熵、信息增益和基尼指数。这些属性度量帮助我们分割决策树。

结论

在本文中，我们理解了数据挖掘中的属性选择度量。有三个属性选择度量：熵、信息增益和基尼指数。我们通过示例讨论了每个度量。