数据挖掘中的数值缩减

数据归约过程减少了数据量，使其适合分析。在归约过程中，必须保持数据的完整性，并减少数据量。可以使用许多技术进行数据归约，数据归约的两种主要方法是降维和数量减少。

什么是数量减少？

在数量减少中，通过选择替代的、较小形式的数据表示来减小数据量。这些技术可以是参数的，也可以是非参数的。对于参数方法，模型可以估计数据，这样只需要保存数据参数，而不是实际数据，例如，对数线性模型。非参数方法用于存储数据的减少表示，包括直方图、聚类和采样。

数量减少的类型

此方法使用替代的、较小形式的数据表示，从而减小数据量。数量减少有两种类型，如下所示：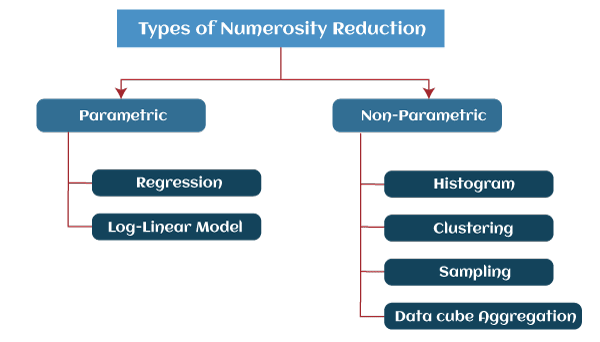

1. 参数

此方法假设一个模型来拟合数据。数据模型参数被估计，并且只存储这些参数，其余数据被丢弃。回归和对数线性方法用于创建此类模型。例如，如果数据适合线性回归模型，则可以使用回归模型来实现参数减少。

• 回归：回归可以是简单线性回归或多元线性回归。当只有一个自变量时，这种回归模型称为简单线性回归。如果有多个自变量，则此类回归模型称为多元线性回归。
  线性回归对数据集的两个属性之间的线性关系进行建模。我们需要在两个属性 x 和 y 之间拟合一个线性回归模型，其中 y 是因变量，x 是自变量或预测变量。模型可以表示为方程 y=wx+b，其中 w 和 b 是回归系数。多元线性回归模型允许我们用多个预测变量来表示属性 y。
• 对数线性模型：对数线性模型可用于基于较小子集维度组合来估计多维空间中每个数据点的概率，这些数据点具有一组离散化的属性。这允许从低维属性构建高维数据空间。对数线性模型发现两个或多个离散属性之间的关系。假设我们有一组 n 维空间中的元组；对数线性模型有助于推导出该 n 维空间中每个元组的概率。

注意：回归和对数线性模型都可以用于稀疏数据，尽管它们的应用可能受到限制。

2. 非参数

非参数数量减少技术不假设任何模型。非参数技术可实现更均匀的减少，而与数据大小无关，但它可能无法像参数方法那样实现大量数据减少。至少有四种非参数数据归约技术，即直方图、聚类、采样、数据立方体聚合、数据压缩。

• 直方图：直方图是根据频率表示的数据。它使用分箱来近似数据分布，是一种流行的数据归约形式。假设一个属性 A 的直方图，并将 A 的数据分布划分为不相交的子集或存储桶。如果每个存储桶仅定义一个属性值或频率对，则这些存储桶称为单例存储桶。
• 聚类：聚类技术将数据元组视为对象。它们将对象分区为组或簇，使得簇内对象彼此“相似”，而与其他簇中的对象“不相似”。它通常根据对象在空间中的“接近”程度来定义，基于距离函数。
  簇的质量可以由其直径定义，即簇中任意两个对象之间的最大距离。质心距离是簇质量的替代度量。它表示每个簇对象到簇质心的平均距离，该质心表示簇的“平均对象”或该区域的平均点。
• 采样：采样可用作数据归约方法，因为它允许通过更小的随机样本或信息子集来定义大型数据集。采样可以将大型数据集减少为较小的样本数据集，以表示原始数据集。有四种采样数据归约方法。
  1. 无放回简单随机抽样（大小）
  2. 放回简单随机抽样（大小）
  3. 整群抽样
  4. 分层抽样
• 数据立方体聚合：数据立方体聚合涉及将数据从详细级别移至较少维度。结果数据集的数据量较小，并且在必要的数据分析任务信息方面没有损失。
  数据立方体聚合是一种多维聚合，它使用数据立方体不同级别的聚合来表示原始数据集，从而实现数据归约。数据立方体聚合，其中数据立方体是存储数据的更有效方式，从而实现数据归约，此外还可以加快聚合操作。
• 数据压缩：它通过修改、编码或转换数据结构以占用更少空间来实现。数据压缩涉及通过消除冗余并以二进制形式表示数据来构建信息的紧凑表示。可以从其压缩形式成功恢复的数据称为无损压缩。相反，无法从压缩形式恢复原始形式的情况称为有损压缩。

数量减少与降维的区别

数据归约有两种主要方法：降维和数量减少。

在降维中，使用数据编码或转换来访问原始数据的减少或“压缩”表示。如果可以在没有任何数据丢失的情况下从压缩数据中重新生成原始数据，则称数据归约为无损。如果重构的数据仅是原始数据的近似值，则称数据归约为有损。

让我们比较降维和数量减少，例如：