数据挖掘中的FP增长算法2025年03月17日 | 阅读 9 分钟 在数据挖掘中,在大规模数据库中寻找频繁模式非常重要,并且在过去几年中得到了广泛的研究。然而,这项任务计算成本很高,尤其是在存在许多模式的情况下。 FP-Growth算法由Han等人提出。这是一种通过模式片段增长来挖掘完整频繁模式集的有效且可扩展的方法,使用了扩展的前缀树结构来存储有关频繁模式的压缩和关键信息,称为频繁模式树(FP-tree)。在他的研究中,Han证明了他的方法优于其他流行的频繁模式挖掘方法,例如Apriori算法和TreeProjection。在一些后续工作中,已经证明FP-Growth比包括Eclat和Relim在内的其他方法表现更好。FP-Growth算法的流行性和效率促成了许多提出其变种以提高其性能的研究。 什么是FP Growth算法?FP-Growth算法是一种无需生成候选集即可查找频繁项集的替代方法,从而提高了性能。为此,它使用分治策略。该方法的核心是使用一种称为频繁模式树(FP-tree)的特殊数据结构,该数据结构保留了项集关联信息。 该算法的工作原理如下: - 首先,它压缩输入数据库,创建FP-tree实例来表示频繁项。
- 在此第一步之后,它将压缩的数据库划分为一组条件数据库,每个数据库与一个频繁模式相关联。
- 最后,每个这样的数据库都会被单独挖掘。
通过这种策略,FP-Growth通过递归地查找短模式然后将它们连接成长频繁模式来减少搜索成本。 在大型数据库中,将FP树保留在主内存中是不可能的。应对此问题的一种策略是将数据库划分为一组较小的数据库(称为投影数据库),然后从每个较小的数据库中构建FP树。 FP-Tree频繁模式树(FP-tree)是一种紧凑的数据结构,用于存储数据库中频繁模式的定量信息。每个事务都被读取,然后映射到FP树中的一条路径。直到所有事务都被读取。具有共同子集的不同事务允许树保持紧凑,因为它们的路径会重叠。 频繁模式树由数据库的初始项集构成。FP树的目的是挖掘最频繁的模式。FP树的每个节点代表一个项集中的项。 根节点代表null,而较低的节点代表项集。在形成树的过程中,节点与较低节点(即项集与其他项集)的关联得以保持。 Han将FP-tree定义为如下所示的树结构: - 一个根节点标记为“null”,其子节点是一组项前缀子树和一个频繁项头表。
- 项前缀子树中的每个节点都包含三个字段:
- 项名称:记录节点代表的项;
- 计数:到达节点的部分路径所代表的事务数;
- 节点链接:链接到FP树中具有相同项名称的下一个节点,如果没有则为null。
- 频繁项头表中的每个条目包含两个字段:
- 项名称:与节点相同;
- 节点链接的头部:指向FP树中第一个带有项名称的节点的指针。
此外,频繁项头表可以包含项的计数支持。下面的图示了一个最佳情况的示例,当所有事务具有相同的项集时,FP树的大小将只有一条节点分支。 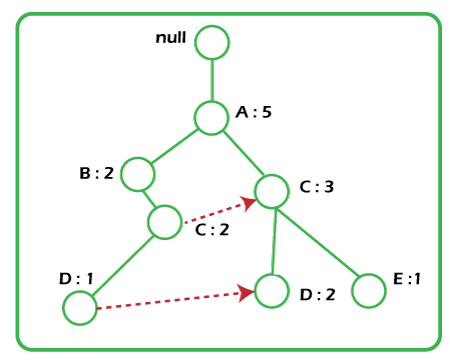 最坏情况发生在每个事务都具有唯一的项集时。因此,存储树所需的空间大于存储原始数据集的空间,因为FP树需要额外的空间来存储节点之间的指针和每个项的计数器。下面的图显示了最坏情况的FP树可能的样子。正如你所见,树的复杂性随着每个事务的独特性而增长。  Han的算法Han定义的构建FP-Tree的原始算法如下: 算法1:FP-tree构建 输入:事务数据库DB和一个最小支持阈值? 输出:FP-tree,DB的频繁模式树。 方法:FP-tree的构建如下。 - 第一步是扫描数据库以查找数据库中项集的出现次数。此步骤与Apriori的第一步相同。1-项集的数据库计数称为支持计数或1-项集的频率。
- 第二步是构建FP树。为此,创建树的根节点。根节点表示为null。
- 下一步是再次扫描数据库并检查事务。检查第一个事务并找出其中的项集。具有最大计数的项集位于顶部,然后是具有较低计数的下一个项集。这意味着树的分支是按照计数降序构建的事务项集。
- 检查数据库中的下一个事务。项集按计数降序排序。如果此事务的任何项集已存在于另一个分支中,则该事务分支将与根节点共享一个公共前缀。
这意味着公共项集链接到此事务中另一个项集的新节点。 - 另外,项的计数会随着其在事务中出现而增加。公共节点和新节点的计数在创建并根据事务链接时会增加1。
- 下一步是挖掘创建的FP树。为此,首先检查最低的节点,以及最低节点的链接。最低节点代表长度为1的频率模式。从这里,沿着FP树中的路径进行遍历。这条路径或这些路径称为条件模式基。
条件模式基是一个子数据库,由FP树中与最低节点(后缀)一起出现的前缀路径组成。 - 构建一个条件FP树,由路径中项集的计数构成。满足阈值支持的项集在条件FP树中被考虑。
- 频繁模式是从条件FP树生成的。
使用此算法,FP树在两次数据库扫描中构建。第一次扫描收集和排序频繁项集,第二次构建FP-Tree。 示例 支持阈值=50%,置信度=60% 表 1 | 交易 | 项目列表 |
|---|
| T1 | I1,I2,I3 | | T2 | I2,I3,I4 | | T3 | I4,I5 | | T4 | I1,I2,I4 | | T5 | I1,I2,I3,I5 | | T6 | I1,I2,I3,I4 |
解决方案:支持阈值=50% => 0.5*6= 3 => min_sup=3 表2:每个项目的计数 表3:按降序对项集进行排序。 构建FP Tree 让我们按照以下步骤构建FP树: - 考虑根节点为null。
- 第一次扫描事务T1:I1, I2, I3 包含三个项目 {I1:1}, {I2:1}, {I3:1},其中I2作为子节点链接,I1链接到I2,I3链接到I1。
- T2:I2, I3, I4 包含I2, I3, I4,其中I2链接到根节点,I3链接到I2,I4链接到I3。但该分支将共享已在T1中使用的I2节点。
- 将I2的计数增加1,I3作为子节点链接到I2,I4作为子节点链接到I3。计数为 {I2:2}, {I3:1}, {I4:1}。
- T3:I4, I5。类似地,创建了一个新的分支,I5作为子节点链接到I4。
- T4:I1, I2, I4。顺序将是I2, I1, I4。I2已链接到根节点。因此,它将增加1。同样,I1将增加1,因为它已与T1中的I2链接,因此 {I2:3}, {I1:2}, {I4:1}。
- T5:I1, I2, I3, I5。顺序将是I2, I1, I3, I5。因此 {I2:4}, {I1:3}, {I3:2}, {I5:1}。
- T6:I1, I2, I3, I4。顺序将是I2, I1, I3, I4。因此 {I2:5}, {I1:4}, {I3:3}, {I4 1}。
 FP树的挖掘总结如下: - 最低节点项I5不被考虑,因为它没有达到最小支持计数。因此被删除。
- 下一个较低的节点是I4。I4出现在2个分支中,{I2,I1,I3:,I41},{I2,I3,I4:1}。因此,以I4为后缀,前缀路径将是{I2, I1, I3:1}, {I2, I3: 1},这构成了条件模式基。
- 条件模式基被视为事务数据库,并构建FP树。这将包含{I2:2, I3:2},I1不被考虑,因为它不满足最小支持计数。
- 该路径将生成所有频繁模式的组合:{I2,I4:2},{I3,I4:2},{I2,I3,I4:2}
- 对于I3,前缀路径将是:{I2,I1:3},{I2:1},这将生成一个2节点FP树:{I2:4, I1:3},并生成频繁模式:{I2,I3:4}, {I1:I3:3}, {I2,I1,I3:3}。
- 对于I1,前缀路径将是:{I2:4},这将生成一个单节点FP树:{I2:4},并生成频繁模式:{I2, I1:4}。
| 项目 | 条件模式基 | 条件FP树 | 生成的频繁模式 |
|---|
| I4 | {I2,I1,I3:1},{I2,I3:1} | {I2:2, I3:2} | {I2,I4:2},{I3,I4:2},{I2,I3,I4:2} | | I3 | {I2,I1:3},{I2:1} | {I2:4, I1:3} | {I2,I3:4}, {I1:I3:3}, {I2,I1,I3:3} | | I1 | {I2:4} | {I2:4} | {I2,I1:4} |
下图描绘了与条件节点I3关联的条件FP树。  FP-Growth算法构建FP-Tree后,就可以对其进行挖掘以找到完整的频繁模式集。Han提出了一组引理和性质来完成这项工作,然后描述了以下FP-Growth算法。 算法2:FP-Growth 输入:数据库DB,由根据算法1构建的FP-tree表示,以及最小支持阈值? 输出:完整的频繁模式集。 方法:调用FP-growth(FP-tree, null)。 当FP-tree包含单个前缀路径时,完整的频繁模式集可以分为三部分生成: - 单个前缀路径P,
- 多路径Q,
- 以及它们的组合(第01至03行和第14行)。
单个前缀路径的结果模式是其子路径的最小支持枚举。之后,定义多路径Q,并处理结果模式。最后,将组合结果作为找到的频繁模式返回。 FP Growth算法的优点FP增长算法的优点如下: - 与Apriori相比,该算法只需要扫描数据库两次,而Apriori在每次迭代中都需要扫描事务。
- 该算法不进行项目配对,使其更快。
- 数据库以紧凑的形式存储在内存中。
- 它对于挖掘长短频繁模式都高效且可扩展。
FP-Growth算法的缺点该算法也存在一些缺点,例如: - FP Tree比Apriori更繁琐,构建起来更困难。
- 它可能很昂贵。
- 当数据库很大时,该算法可能不适合共享内存。
Apriori和FP Growth算法的区别Apriori和FP-Growth算法是最基本的FIM算法。这些算法之间存在一些基本差异,例如: | Apriori | FP Growth |
|---|
| Apriori通过配对生成频繁模式,例如单项集、双项集和三项集。 | FP Growth生成FP-Tree来生成频繁模式。 | | Apriori使用候选生成,其中频繁子集一次扩展一个项目。 | FP-growth为数据中的每个项目生成一个条件FP-Tree。 | | 由于Apriori在每个步骤中都会扫描数据库,因此对于项目数量较多的数据,它会变得耗时。 | FP-tree在其初始步骤中只需要一次数据库扫描,因此消耗的时间更少。 | | 数据库的转换版本保存在内存中 | 为每个项目保存一组条件FP-tree保存在内存中 | | 它使用广度优先搜索 | 它使用深度优先搜索。 |
|



