消除上下文无关文法的歧义

在编译的语法分析阶段，编程语言构造是在上下文无关语法中指定的。上下文无关语法可以生成形式语言的所有可能的字符串。给定一个语法，该语法可以生成的所有字符串（来自词法分析的token字符串）都称为格式良好，为了检查这一点，解析器构建一个解析树。

如果语法是模棱两可的，则没有一个解析器可以接受它。 什么是歧义？

让我们迈出小步

你需要了解的关于上下文无关语法的一切

其中

V：非终结符 (S, A, B, C...)

T：终结符-> 字符串符号 (a, b, c...)

P：产生式规则 (非终结符 -> 0 个或多个终结符或非终结符。

例如，A -> aA/a)

S：开始符号 (一个非终结符)

在编写语法之前，需要了解以下术语

推导： 替换产生式规则体中的非终结符以获得字符串。这些终结符字符串构成了语法的语言。

例如

语言： 所有具有平衡的开括号和闭括号的字符串。

语法： S -> (S) S/ε

产生式体中的非终结符：S

假设给定的输入字符串是 w = (((())))

推导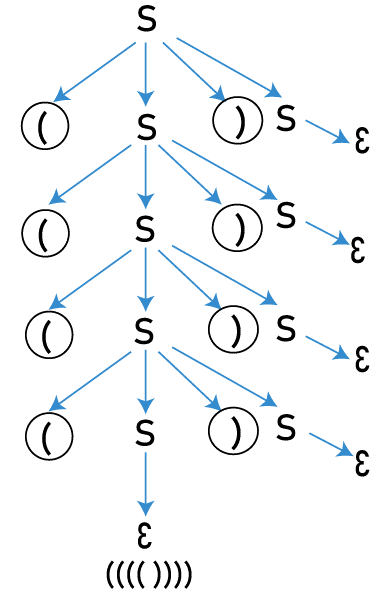

这种表示称为 推导树/解析树。

如果一个输入字符串有多个解析树，则该语法被称为“有歧义的”。

注意：每个语法都将有一个最左推导树和一个最右推导树。有歧义的语法是指具有多个最左推导树或多个最右推导树的语法。

通常，在语法分析中生成的解析树会传递到编译的其余部分，但是如果一个字符串具有多个解析树，则编译器将无法确定要考虑哪个解析树。

让我们举个例子

语法

输入字符串： id + id* id

最左推导可以通过两种方式完成

对于给定的输入字符串，我们得到了两个最左推导树。我们需要消除语法中的歧义。

消除CFG语法中的歧义

并非所有语法中的歧义都可以消除。没有直接和官方的算法可以确定给定的语法是否含糊不清。我们需要通过构建所有可能的解析树来检查。我们可以使用 优先级和结合性 从某些语法中删除歧义。

让我们举个例子

语法

这里 var 可以是任何变量，const 可以是任何常量值。字符串 a - b - c 有两个最左推导

例如，如果我们取值 a = 2，b = 3 和 c = 4

a - b - c = 2 - 3 - 4 = -5

在第一个推导树中，根据替换顺序，表达式将被计算为

(a - b) - c = (2 - 3) - 4 = -1 -4 = -5

在第二个推导树中：a - (b - c) = 2 - (3 - 4) = 2 - -1 = 3

观察到两个解析树都没有给出相同的值。它们有不同的含义。在上面的示例中，第一个推导树是语法的正确解析树。

(a - b) - c。这里表达式中有两个相同的运算符。根据数学规则，必须根据所用运算符的结合性来评估表达式。在上面的示例中，运算符为 -，它给出从左到右的结合性。因此，第一个推导树是正确的解析树。

因此，对于从左到右关联运算符，解析树必须是左关联的 - 左子树上的非终结符必须首先被推导出来，然后是右子树。

注意：对于像 ^ 这样的从右到左关联的运算符，必须使语法具有右关联性，因为对于这些表达式，求值顺序必须从右到左。

现在，让我们将语法转换为无歧义语法

我们需要使语法具有左递归性。我们需要用一个随机的非终结符替换右侧的非终结符

现在，对于字符串 a - b - c

现在，如果语法是

对于字符串 id + id * id*，此语法将给出两个最左推导树。

我们不能在这里使用结合性，因为有两种不同的运算符，+ 和 *。因此，我们需要使用“优先级”。

在字符串中

求值的顺序必须是：id + (id * id)，因为 * 的优先级高于 +。 具有最高优先级的运算符必须首先求值。因此，具有高优先级的运算符应安排在解析树的较低级别。

如果 id = 2

如果 + id * id = 2 + 2 * 2 = 6

对于第一个推导树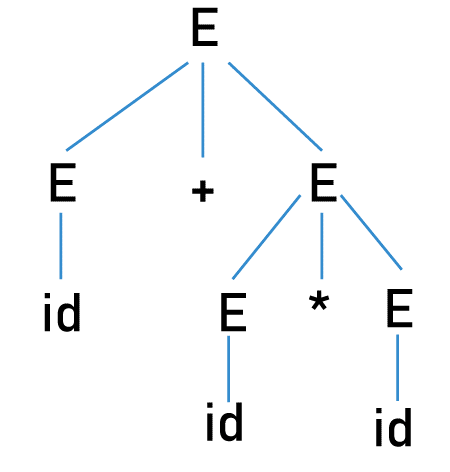

id + (id * id) = 2 + (2 * 2) = 2 + 4 = 6

对于第二个推导树

(id + id) * id = (2 + 2) * 2 = 4*2 = 8

因此，第一个推导树是正确的解析树。

转换为无歧义语法

我们应该编写语法，以便所有优先级最高的运算符都保留在较低级别。每个产生式都应遵循基于所用运算符的结合性的递归。

• +, -, *, / 是左结合运算符。因此，使用这些运算符的产生式必须遵循左递归
• ^ 和 = 是右结合运算符。因此，使用这些运算符的产生式必须遵循右递归。

给定文法

优先级： * 比 + 具有最高优先级。因此，它应该在较低的级别。因此，我们需要从 + 开始

结合性： + 和 * 都是左结合的

解析树

现在，最后，让我们再举一个例子

首先，确定给定的语法是否含糊不清。

给定一个字符串 id + id * id ^ id

E -> E + E

id + E * E

id + id * E

id + id * E^E

id + id * id ^ id

E -> E * E

E + E * E

id + E * E

id + id * E ^ E

id + id * id ^ id

多个最左推导树。

运算符： +, * 和 ^

优先级 ^ > * > +

结合性

+, * -> 从左到右

^ -> 从右到左

• 我们需要安排语法，以便具有 ^ 和 * 的产生式位于解析树的较低级别，并且每个产生式必须遵循其运算符的结合性。

语法

E -> E + P/P

P -> P * Q/Q

Q -> R ^ Q/R (右结合)

R -> id

语法树

求值

如果 id = 2: id + id * id ^ id = 2 + 2 * 2² = 2 + 2 * 4 = 16

要记住的重要点

1. 在检查语法是否含糊不清时，我们必须仔细考虑一个字符串。含糊语法的某些字符串可能并不含糊不清。
2. 在消除歧义的过程中，请勿更改语法。我们不应更改原始语言，而应使用非终结符，以使语法的含义不被更改。