解析树2025 年 5 月 26 日 | 阅读 5 分钟
解析树遵循这些要点
构建解析树的规则要构造解析树,我们需要遵循一组规则。这些规则确保解析树正确表示程序的句法结构。 以下是构造解析树的主要规则
解析树的属性
示例推导规则 输入 a * b + c 步骤 1 步骤 2 步骤 3 步骤 4 步骤 5 解析树的结构取决于产生式规则的顺序和选择。 因此,可以通过“最左”或“最右”推导来获得推导。 让我们详细解释每一个
例如 考虑具有产生式的语法 G S -> aSS | b 用最左和最右推导推导出字符串“aababbb”。 最左推导 S -> aSS S -> aaSSS S -> aabSS S -> aabaSSS S -> aababSS S -> aababbS S -> aababbb 最右推导 S -> aSS S -> aSb S -> aaSSb S -> aaSaSSb S -> aaSaSbb S -> aaSabbb S -> aababbb 解析技术解析器使用不同的技术进行解析,例如  自顶向下解析器:它从开始符号开始构建解析树,并继续进行到请求的字符串,方法是将每个非终结符替换为其相应的 R.H.S 部分。 它在解析树的构造中使用最左推导。 例如 输入字符串:xxxxyzz 产生式规则集是 S -> xxW S -> y W -> SZ  自底向上解析器:当解析树可以从叶子构建到根时,这种类型的解析器称为自底向上解析器。 它从给定的字符串开始,一直进行到起始符号。 它以相反的顺序使用从右到左的推导来构造解析树。 例如 1 输入字符串:xxxxyzz 产生式规则集是 S -> xxxxyzz // S - > y S -> xxxxSzz // W - > Sz S -> xxxxwz // S - > xxW S -> xxSz // W - > Sz S -> xxW // S - > XXW 以上字符串有效,因为它是由解析树生成的。 例如 2 输入字符串:id * id + id 产生式规则集是 E -> E + E E -> E * E E -> id  在每个归约步骤中,匹配产生式右侧的特定子字符串被替换为该产生式左侧的符号,并且如果子字符串在每一步都选择正确,则反向追踪最右推导。 例如 输入字符串:abcde 产生式规则集是 S -> aABe A -> Abc | b B -> d  自顶向下解析的缺点1. 自顶向下解析存在几个问题,例如左递归。 如果一个语法具有非终结符 "A",则存在推导,则称该语法为左递归。 A -> Aα;对于一些 α 左递归语法可能导致自顶向下解析器进入无限循环。 2. 自顶向下解析的第二个问题是回溯。  消除左递归假设一个语法为 A -> Aα | β,那么可以通过以下方式消除左递归 A -> Aα | β A -> βA' A' -> αA' | ε 例如 1 从语法中消除左递归 E -> E + T | T // (A -> Aα | β) E -> TE' E' -> +TE' | ε 例如 2 从语法中消除左递归 Q -> Q * R | R // (A -> Aα | β) Q -> RQ' Q' -> *RQ' | ε 例如 3 从语法中删除左递归 S -> Aa A -> Sd | a 间接左递归 解决方案 S -> Aa A -> Aad | a //(直接左递归) 比较 W A -> Aα | β α = ad, β = a A -> aA' A' -> adA' | ε 更新的语法 S -> Aa A -> aA' A' -> adA' | ε 左因子分解这是一个提取选项的公共前缀的过程。 它是一个将 2 个产生式的公共部分隔离到单个产生式的过程。 任何形式的产生式 A -> αβ1 | αβ2 | αβ3 ___ | αβn 可以用以下方式替换 A -> αA' A -> β1 | β2 | β3 ___ | βn 例如 从以下语法中删除左因子分解。 A -> aA | aAB | a B -> bB | bA 解决方案 A -> aA' B -> bB' A' -> A | AB | ε B -> B | A 关于解析树的常见问题1. 您是什么意思的解析树? 上下文无关文法生成的字符串可以通过称为树的分层结构来表示。 这样的树代表推导,因此称为解析树/推导树和语法树。 2. 您是什么意思的歧义语法? 具有多个树的语法称为歧义语法。 例如:为给定的字符串“a + a * b”创建解析树 产生式规则集是 S -> S + S S -> S * S S -> a S -> b 解析树,例如 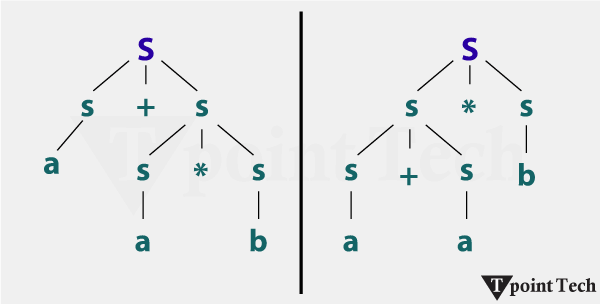 下一主题歧义 |
我们请求您订阅我们的新闻通讯以获取最新更新。