TM 示例

示例 1

构造一个接受语言 L = {0ⁿ1ⁿ2ⁿ} 的 TM，其中 n≥1

解决方案

L = {0ⁿ1ⁿ2ⁿ | n≥1} 表示一种语言，其中我们只使用 3 种字符，即 0、1 和 2。在此语言中，一定数量的 0 后跟相同数量的 1，然后再跟相同数量的 2。任何属于此类的字符串都将被此语言接受。

001122 的模拟如下所示

现在，我们将看到这个图灵机如何处理 001122。最初，状态为 q0，磁头指向 0，如下所示

移动将是 δ(q0, 0) = δ(q1, A, R)，这意味着它将转到状态 q1，将 0 替换为 A，磁头将向右移动，如下所示

移动将是 δ(q1, 0) = δ(q1, 0, R)，这意味着它不会改变任何符号，保持在同一状态并向右移动，如下所示

移动将是 δ(q1, 1) = δ(q2, B, R)，这意味着它将转到状态 q2，将 1 替换为 B，磁头将向右移动，如下所示

移动将是 δ(q2, 1) = δ(q2, 1, R)，这意味着它不会改变任何符号，保持在同一状态并向右移动，如下所示

移动将是 δ(q2, 2) = δ(q3, C, R)，这意味着它将转到状态 q3，将 2 替换为 C，磁头将向右移动，如下所示

现在，移动 δ(q3, 2) = δ(q3, 2, L) 和 δ(q3, C) = δ(q3, C, L) 和 δ(q3, 1) = δ(q3, 1, L) 和 δ(q3, B) = δ(q3, B, L) 和 δ(q3, 0) = δ(q3, 0, L)，然后移动 δ(q3, A) = δ(q0, A, R)，这意味着它将转到状态 q0，将 A 替换为 A，磁头将向右移动，如下所示

移动将是 δ(q0, 0) = δ(q1, A, R)，这意味着它将转到状态 q1，将 0 替换为 A，磁头将向右移动，如下所示

移动将是 δ(q1, B) = δ(q1, B, R)，这意味着它不会改变任何符号，保持在同一状态并向右移动，如下所示

移动将是 δ(q1, 1) = δ(q2, B, R)，这意味着它将转到状态 q2，将 1 替换为 B，磁头将向右移动，如下所示

移动将是 δ(q2, C) = δ(q2, C, R)，这意味着它不会改变任何符号，保持在同一状态并向右移动，如下所示

移动将是 δ(q2, 2) = δ(q3, C, L)，这意味着它将转到状态 q3，将 2 替换为 C，磁头将向左移动，直到我们到达 A，如下所示

B 前面是 A，这意味着所有的 0 都被标记为 A。所以我们将向右移动以确保没有 1 或 2 存在。移动将是 δ(q2, B) = (q4, B, R)，这意味着它将转到状态 q4，不会改变任何符号，并向右移动，如下所示

移动将是 (q4, B) = δ(q4, B, R) 和 (q4, C) = δ(q4, C, R)，这意味着它不会改变任何符号，保持在同一状态并向右移动，如下所示

移动 δ(q4, X) = (q5, X, R) 意味着它将转到状态 q5，即 HALT 状态，而 HALT 状态对于任何 TM 始终是接受状态。

同一个 TM 可以用转换图表示

示例 2

构造一个 TM 来检查偶数长度字符串的回文串。

解决方案

首先，我们读取左边的第一个符号，然后将其与右边的第一个符号进行比较，以检查它们是否相同。

再次，我们比较左边的第二个符号和右边的第二个符号。我们对所有符号重复此过程。如果我们发现任何符号不匹配，我们就不能将机器导向 HALT 状态。

假设字符串是 ababbabaΔ。ababbabaΔ 的模拟如下所示

现在，我们将看到这个图灵机如何处理 ababbabaΔ。最初，状态为 q0，磁头指向 a，如下所示

我们将用 * 标记它，并向右移动以搜索 a，如下所示

我们将一直向右移动直到 Δ，如下所示

我们将向左移动并检查它是否是 a

它是 'a'，所以将其替换为 Δ 并向左移动，如下所示

现在向左移动直到 *，如下所示

向右移动并读取它

现在将 b 转换为 * 并向右移动，如下所示

向右移动直到 Δ 以搜索 b，如下所示

向左移动，如果符号是 b，则将其转换为 Δ，如下所示

现在向左移动直到 *，如下所示

将 a 替换为 * 并向右移动直到 Δ，如下所示

我们将向左移动并检查它是否是 a，然后将其替换为 Δ，如下所示

它是 'a'，所以将其替换为 Δ，如下所示

现在向左移动直到 *

向右移动，如下所示

将 b 替换为 * 并向右移动直到 Δ，如下所示

向左移动，如果左边的符号是 b，则将其替换为 Δ，如下所示

向左移动直到 *

向右移动并检查它是否是 Δ

转到 HALT 状态

同一个 TM 可以用转换图表示

示例 3

构造一个 TM 来检查奇数长度字符串的回文串。

解决方案

首先，我们读取左边的第一个符号，然后将其与右边的第一个符号进行比较，以检查它们是否相同。

再次，我们比较左边的第二个符号和右边的第二个符号。我们对所有符号重复此过程。如果我们发现任何符号不匹配，我们就将机器导向 HALT 状态。

假设字符串是 00100Δ。00100Δ 的模拟如下所示

现在，我们将看到这个图灵机如何处理 00100Δ。最初，状态为 q0，磁头指向 0，如下所示

现在将 0 替换为 * 并向右移动，如下所示

向右移动直到 Δ，如下所示

向左移动并将 0 替换为 Δ 并向左移动

现在向左移动直到 *，如下所示

向右移动，将 0 转换为 *，然后向右移动，如下所示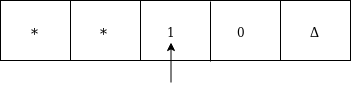

向右移动直到 Δ

向左移动并将 0 替换为 Δ，如下所示

向左移动直到 *，如下所示

向右移动并将 1 转换为 *，如下所示

向左移动

因为它是 *，转到 HALT 状态。

同一个 TM 可以用转换图表示

示例 4

构造 TM 来计算一元数系统中的加法函数。

解决方案

一元数只由一种字符组成，即 1。数字 5 可以用一元数系统写成 11111。在这个 TM 中，我们将执行两个一元数的加法。

例如

2 + 3
即 11 + 111 = 11111

如果您观察到此加法过程，您会发现它与字符串连接函数有相似之处。

在这种情况下，我们只需将 + 替换为 1，然后向右移动以搜索字符串的末尾，我们将最后一个 1 转换为 Δ。

输入 3+2

111+11Δ 的模拟如下所示

向右移动直到 + 号，如下所示

将 + 转换为 1 并向右移动，如下所示

现在，向右移动

再次向右移动

现在遇到了 Δ，所以只需向左移动，如下所示

将 1 转换为 Δ

因此，磁带现在包含两个一元数的加法结果。

TM 的外观如下

在这里，我们实现了 f(a + b) = c 的函数。我们假设 a 和 b 都是非零元素。

示例 5

构造一个 TM 来计算两个一元数的减法 f(a-b) = c，其中 a 始终大于 b。

解决方案： 这里我们有一些假设，即第一个数字大于第二个数字。让我们假设 a = 3，b = 2，所以输入磁带将是

我们将向右移动到 - 号，然后执行从第一个数字中减去一定数量的 1。让我们看模拟以理解逻辑

向右移动直到 -，如下所示

向右移动并将 1 转换为 *，如下所示

现在向左移动

再次向左移动

将 1 转换为 * 并向右移动

现在向右移动直到 1

将 1 转换为 * 并向左移动

将 1 转换为 * 并移动

向右移动直到 Δ，如下所示

现在我们在 HALT 状态。

因此，我们在输入磁带上得到 1 作为 f(3-2) 的答案。

图灵机的外观如下