深度神经网络中的前馈过程

现在，我们知道如何通过具有不同权重和偏差的线的组合来产生非线性模型。 神经网络如何知道在每一层中使用什么权重和偏差值？ 这与我们对基于单神经元的感知器模型所做的没有什么不同。

我们仍然使用梯度下降优化算法，该算法通过迭代地朝着最陡下降的方向移动来最小化模型的误差，该方向更新我们模型的参数，同时确保最小的误差。 它更新每一层中每个模型的权重。 稍后我们将更多地讨论优化算法和反向传播。

重要的是要认识到我们神经网络的后续训练。 识别是通过一些决策边界划分我们的数据样本来完成的。

“接收输入以产生某种输出以进行某种预测的过程称为前馈。” 前馈神经网络是许多其他重要神经网络（例如卷积神经网络）的核心。

在前馈神经网络中，网络中没有任何反馈回路或连接。 这里只有一个输入层、一个隐藏层和一个输出层。

可以有多个隐藏层，这取决于你处理的数据类型。 隐藏层的数量称为神经网络的深度。 深度神经网络可以从更多函数中学习。 输入层首先为神经网络提供数据，然后输出层根据一系列函数对该数据进行预测。 ReLU 函数是深度神经网络中最常用的激活函数。

为了扎实理解前馈过程，让我们在数学上看看它。

1) 第一个输入被馈送到网络，表示为矩阵 x1、x2 和 1，其中 1 是偏差值。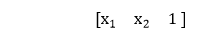

2) 每个输入都乘以权重，相对于第一个和第二个模型，以获得它们在每个模型中处于正区域的概率。

因此，我们将使用矩阵乘法将我们的输入乘以权重矩阵。

3) 之后，我们将取分数的 sigmoid，它会给我们点在两个模型中处于正区域的概率。

4) 我们将上一步获得的概率乘以第二组权重。 在采用输入组合时，我们总是包含一个偏差 1。

并且正如我们所知，为了获得该点位于该模型的正区域的概率，我们取 sigmoid，从而在前馈过程中产生我们的最终输出。

让我们采用我们之前拥有的神经网络，该网络具有以下线性模型和隐藏层，它们组合起来以在输出层中形成非线性模型。

那么，我们将做什么呢？ 我们使用我们的非线性模型来产生一个输出，该输出描述了该点位于正区域的概率。 该点由 2 和 2 表示。 连同偏差，我们将输入表示为

隐藏层中的第一个线性模型回忆一下，并且该方程定义了它

这意味着在第一层中，为了获得线性组合，输入乘以 -4、-1，偏差值乘以 12。

输入的权重乘以 -1/5、1，偏差乘以 3 以获得该点在我们第二个模型中的线性组合。

现在，为了获得该点相对于两个模型都位于正区域的概率，我们将 sigmoid 应用于两个点，如下所示

第二层包含权重，这些权重决定了第一层中线性模型的组合，以获得第二层中的非线性模型。 权重为 1.5、1，偏差值为 0.5。

现在，我们必须将第一层的概率乘以第二组权重，如下所示

现在，我们将取最终分数的 sigmoid

这是前馈过程背后的完整数学原理，其中来自输入的输入遍历神经网络的整个深度。 在此示例中，只有一个隐藏层。 无论有一个隐藏层还是二十个隐藏层，所有隐藏层的计算过程都是相同的。