向量运算

2025年3月17日 | 阅读 3 分钟

我们知道张量有不同类型的维度，例如零维、一维和多维。向量是一维张量，为了操作它们，有几种运算可用。向量运算有不同的类型，例如数学运算、点积和 linspace。向量在深度学习中起着至关重要的作用。

在深度学习神经网络中，我们借助向量或一维张量生成随机点。以下是可以在向量上执行的操作。

数学运算

我们可以将张量加、减、乘、除另一个张量。以下是在向量上执行的所有数学运算的表，以及预期的输出。

序号。	操作	张量 A	张量 B	数字	语法	输出
1	+	[1, 2, 3]	[4, 5, 6]	2	A+B	[5, 7, 9]
2	+	[1, 2, 3]	[4, 5, 6]	2	A+2	[3, 4, 5]
3	-	[1, 2, 3]	[4, 5, 6]	2	A-B	[-3, -3, -3]
4	-	[1, 2, 3]	[4, 5, 6]	2	B-2	[2, 3, 4]
5	*	[1, 2, 3]	[4, 5, 6]	2	A*B	[4, 10,18]
6	*	[1, 2, 3]	[4, 5, 6]	2	A*2	[2, 4, 6]
7	/	[1, 2, 3]	[4, 5, 6]	2	B/A	[4, 2, 2]
8	/	[1, 2, 3]	[4, 5, 6]	2	B/2	[2, 2, 3]

import torch
A=torch.tensor([1,2,3])
B=torch.tensor([4,5,6])
A+B
A+2
A-B
B-2
A*B
A*2
B/A
B/2

输出

tensor([5, 7, 9])
tensor([3, 4, 5])
tensor([-3, -3, -3])
tensor([2, 3, 4])
tensor([ 4, 10, 18])
tensor([2, 4, 6])
tensor([4, 2, 2])
tensor([2, 2, 3])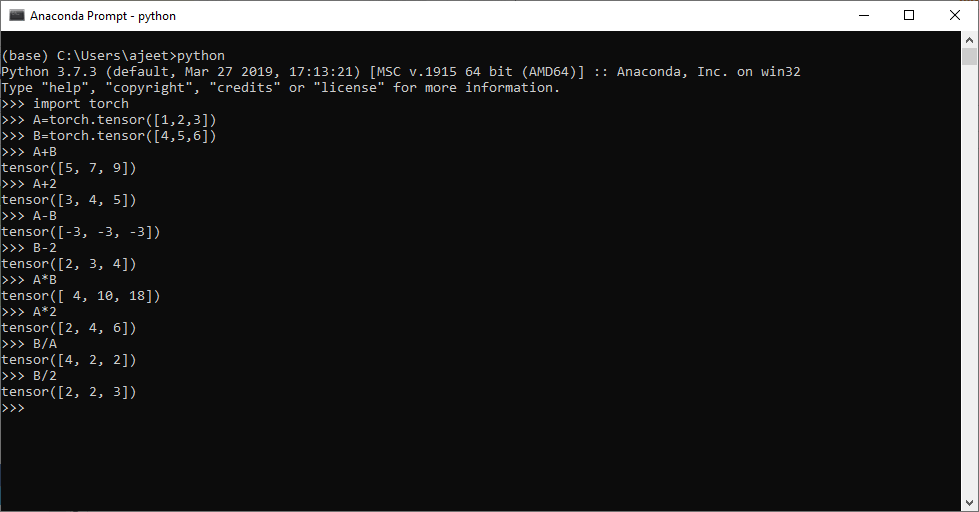

点积和 linspace

我们也可以执行两个张量的点积。我们使用 torch 的 dot() 方法来计算，该方法提供准确或预期的结果。还有另一个向量运算，即 linspace。对于 linspace，我们使用方法 linspace()。此方法包含两个参数，第一个是起始数字，第二个是结束数字。

此方法的输出是，它打印从起始数字到结束数字的 100 个等间距的数字。

注意：我们可以通过传递一个额外的参数（即参数列表末尾的步长）来显式指定步长，而不是使用默认值。

示例

import torch
t1= torch.tensor([1,2,3])
t2= torch.tensor([4,5,6])
DotProduct= torch.dot(t1,t2)
print(DotProduct)
torch.linspace(2,9)

输出

tensor(32)
tensor([2.0000, 2.0707, 2.1414, 2.2121, 2.2828, 2.3535, 2.4242, 2.4949, 2.5657,
        2.6364, 2.7071, 2.7778, 2.8485, 2.9192, 2.9899, 3.0606, 3.1313, 3.2020,
        3.2727, 3.3434, 3.4141, 3.4848, 3.5556, 3.6263, 3.6970, 3.7677, 3.8384,
        3.9091, 3.9798, 4.0505, 4.1212, 4.1919, 4.2626, 4.3333, 4.4040, 4.4747,
        4.5455, 4.6162, 4.6869, 4.7576, 4.8283, 4.8990, 4.9697, 5.0404, 5.1111,
        5.1818, 5.2525, 5.3232, 5.3939, 5.4646, 5.5354, 5.6061, 5.6768, 5.7475,
        5.8182, 5.8889, 5.9596, 6.0303, 6.1010, 6.1717, 6.2424, 6.3131, 6.3838,
        6.4545, 6.5253, 6.5960, 6.6667, 6.7374, 6.8081, 6.8788, 6.9495, 7.0202,
        7.0909, 7.1616, 7.2323, 7.3030, 7.3737, 7.4444, 7.5152, 7.5859, 7.6566,
        7.7273, 7.7980, 7.8687, 7.9394, 8.0101, 8.0808, 8.1515, 8.2222, 8.2929,
        8.3636, 8.4343, 8.5051, 8.5758, 8.6465, 8.7172, 8.7879, 8.8586, 8.9293,
        9.0000])

在二维坐标系上绘制函数

linspace 函数可用于在二维坐标系上绘制函数。对于 x 轴，我们创建一个从 0 到 10 的 linspace，间隔为 2.5，而 Y 将是每个 x 值的一个函数。例如，我们可以找到每个 x 值的指数，作为 y。

现在，我们使用Map plot lib库绘制 x 和 y 数据，该库是用于数据分析的可视化库。

示例

import torch
import numpy as np
import matplotlib.pyplot as plt
x=torch.linspace(0,10,100)
y=torch.exp(x)
plt.plot(x.numpy(),y.numpy())
plt.show()

输出

注意：为了获得更平滑的指数，我们必须增加 linspace 中的数据。如果它是 100 而不是 5，那么输出会更平滑，就像那样。

注意：我们可以绘制 x 的 sin 值而不是指数值。因此，它将创建一个正弦曲线。

示例

im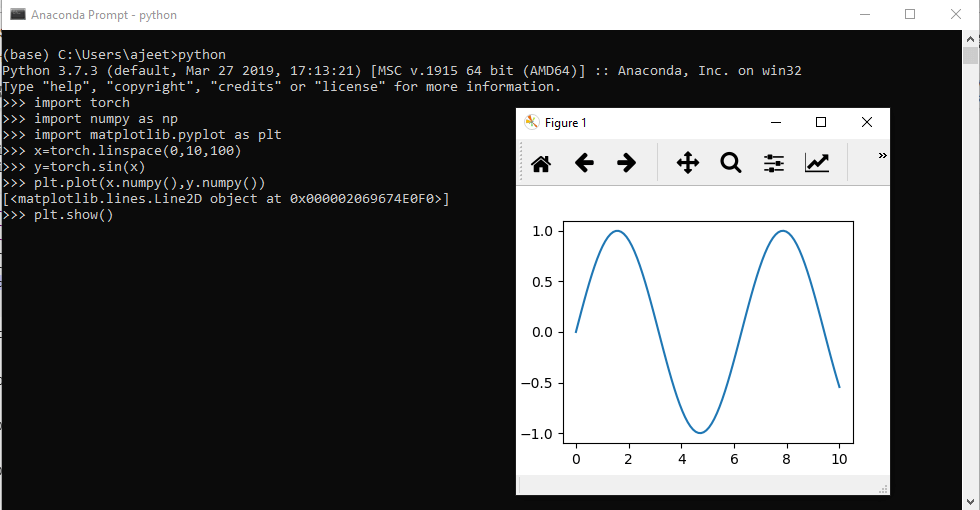port torch
import numpy as np
import matplotlib.pyplot as plt
x=torch.linspace(0,10,100)
y=torch.sin(x)
plt.plot(x.numpy(),y.numpy())
plt.show()

输出

下一主题二维张量

我们提供所有技术（如 Java 教程、Android、Java 框架）的教程和面试问题

联系信息

G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India

hr@tpointtech.com

+91-9599086977

关注我们

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

PyTorch教程

张量

线性回归

感知器

深度神经网络

图像识别

CNN

图像分类

风格迁移

面试题

其他

向量运算

数学运算

点积和 linspace

注意：我们可以通过传递一个额外的参数（即参数列表末尾的步长）来显式指定步长，而不是使用默认值。

示例

在二维坐标系上绘制函数

示例

注意：为了获得更平滑的指数，我们必须增加 linspace 中的数据。如果它是 100 而不是 5，那么输出会更平滑，就像那样。

注意：我们可以绘制 x 的 sin 值而不是指数值。因此，它将创建一个正弦曲线。

示例

相关帖子

二维张量

PyTorch梯度

一维张量

张量介绍

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器