均方误差

均方误差的计算方式与之前的通用损失方程大致相同。我们还将考虑偏差值，因为这也是一个需要在训练过程中更新的参数。

(y-Ax+b)²

均方误差最好用一个例子来解释。

假设我们有一组值，我们首先像之前一样，通过一组随机的权重和偏差值绘制一些回归线参数。

误差对应于实际值与预测值的距离——它们之间的实际距离。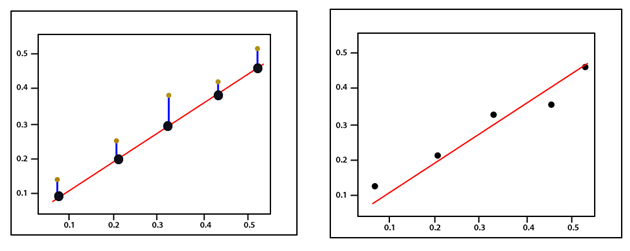

对于每个点，误差的计算方法是将我们的线模型的预测值与实际值进行比较，使用以下公式

每个点都与一个误差相关联，这意味着我们必须对每个点的误差进行求和。我们知道预测可以改写为

由于我们正在计算均方误差，因此我们必须通过除以数据点的数量来取平均值。现在如前所述，误差函数的梯度应该引导我们朝向误差增加最大的方向。

朝着我们成本函数梯度的负方向移动，我们朝向误差最小的方向移动。我们将使用这个梯度作为指南针，始终引导我们向下坡。在梯度下降中，我们忽略了偏差的存在，但对于误差，需要参数 A 和 b 来定义。

现在，我们接下来要做的是计算每个的偏导数，就像之前一样，我们从任何 A 和 b 值对开始。

我们使用梯度下降算法，根据上面提到的两个偏导数，更新 A 和 b，以朝向最小误差的方向前进。对于每次迭代，新的权重等于

A₁=A₀-∝ f'(A)

新的偏差值等于

b₁=b₀-∝ f'(b)

编写代码的主要思想是，我们从一个具有一组随机权重和偏差值参数的随机模型开始。这个随机模型往往具有较大的误差函数、较大的成本函数，然后我们使用梯度下降来更新我们模型的权重，朝向最小误差的方向。最小化该误差以返回优化结果。