卡诺发动机

卡诺发动机是一种理论上的发动机，其工作基于卡诺循环，该循环包含四个不同的阶段。这些阶段描述了热量转化为功的过程。卡诺还指出，发动机需要一个热体，它充当发动机的能源。它将能量传递给冷体，以进行一些机械功。热传递的概念基于热力学第二定律。

在这里，我们将讨论卡诺发动机的历史、能量阶段、效率、卡诺定理、卡诺发动机的例子、卡诺循环等等。

如前所述，卡诺发动机与热力学第二定律有直接关系。

首先，让我们讨论热力学第二定律。

热力学第二定律

热力学第二定律指出，在热力学（物理学的一个分支）系统中存在一个名为熵（S）的热力学变量。

熵 S 的变化定义为热传递变化与温度的比率。它由以下公式给出

我们也可以说，热力学第二定律定义了能量的质量。

让我们看两个例子。

示例 1：如果一个 100 摄氏度的物体与一个 0 摄氏度的相似物体接触，热量将开始从温度较高的物体流向温度较低的物体。这意味着热量将从较热的物体流向较冷的物体，直到两个物体都达到 50 摄氏度。

示例 2：设一个容器分为两部分。一部分装有气体，另一部分是真空（意味着没有气体）。当容器中两个腔之间的阀门打开时，气体将开始流向真空空间，直到气体最终占据容器的两个部分。

这两个例子都描绘了热力学第二定律。

让我们开始讨论卡诺发动机。

在这里，我们将讨论历史、卡诺发动机的效率、卡诺定理、卡诺循环等等。

历史

• 1824 年，法国科学家N L Sadi Carnot首次提出了卡诺发动机作为一个理想化的发动机。
• 1834 年，法国物理学家兼工程师Paul Emile首次扩展了卡诺发动机的图形模型。
• 1857 年，德国数学家兼物理学家 Rudolf Clausis 对该发动机进行了数学探索。
• 它被命名为卡诺发动机。

卡诺发动机的能量阶段

有四个阶段描述了卡诺发动机的过程。描述此过程的图表如下所示

四个状态的示意图如下所示

让我们通过一个例子来定义这些状态。

假设一个气缸与一个高温体 T1 保持接触。首先，该物体与气缸处于压缩状态，这在上面的图中表示为状态'a'。状态'b'表示气体的等温膨胀。在此过程中，功被做，热量在特定温度下被供给物体。设供给的热量和温度分别为Q1和T1。气缸放置在绝热平台上并允许膨胀。它现在已达到阶段'c'。在此阶段，温度开始从 T1 降至 T2。由于“c”阶段的温度下降，气缸现在与低温体接触。它被等温压缩到'd'阶段，如上图所示。

在气体上做功，它将热量(Q2)排斥到温度为T2的物体上。现在将其放置在绝热平台上，并进一步压缩以达到阶段“a”。阶段“a”的温度为 T1。

上面已经表示并解释了循环过程'abcda'。如果活塞无摩擦且始终缓慢移动，该过程也可以是可逆循环过程。

卡诺发动机的效率

卡诺发动机的基本过程如下图所示

它表示压力-体积图。

在这里，T 代表温度，S 代表熵。图上的点 a、b、c 和 d 代表如上所述的状态。设状态下的熵为 S1。在等温过程 ad 中，系统获得的热量为 Q1，温度为 T1。由于向系统施加了热量，熵增加，如

S2 - S1 = Q1/T1 ...(1)

在绝热过程中，bc 和 ad 的熵保持不变，如能量状态中所述。状态“c”下的熵为 S2。我们知道系统在“cd”部分以较低温度 T2 放热 Q2。因此，“d”阶段的熵会降低。“da”部分的熵由于绝热过程而保持不变。由于状态“a”下的熵为 S1，因此在状态“d”下也将相同。

使用熵变化公式，可以表示“cd”过程为

S1 - S2 = -Q2/T2 ...(2)

这是因为与 S1 相比，S2 是熵的减小。

我们也可以写成

S2 - S1 = Q2/T2

比较方程 1 和 2，我们得到

Q1/T1 = Q2/T2

或

Q2/Q1 = T2/T1

卡诺发动机的效率定义为所做功除以能量。

效率 = W/Q1

功是过程中 cd 的能量变化。

效率 = Q1 - Q2 / Q1

= 1 - Q2/Q1

= 1 - T2/T1

因此，我们可以说发动机的效率仅取决于热体和冷体的温度。这是发动机工作的两个物体。

卡诺定理

如前所述，卡诺发动机基于热力学第二定律。它是一种可逆发动机，与其它类型的热机相比，它是一种高效发动机。这意味着在相同两个温度之间工作的可逆发动机具有相等的效率。在相同两个温度之间工作的任何其他发动机的效率都不会超过可逆热机。

上述定理称为卡诺定理。它由以下公式给出

N = 1 - T₂/T₁

卡诺发动机的例子

让我们讨论一个卡诺发动机的日常生活例子，即冰箱。

冰箱里有一个热泵，它执行这个过程。热机的作用是利用来自物体的热量将其转化为功，并将剩余的热量排斥到冷体。冰箱的工作方式与热机相反。冰箱中的热泵将热量从冷体传递并输送到热体。它从冷体吸收一定量的热量，对其进行处理（做功），并将总能量以热量的形式供给加热的物体。我们也可以注意到冰箱周围的环境相当热。

冰箱的过程如下所示

卡诺循环

当一个系统经历一系列不同的状态时，就会发生一个循环。一个循环的一个状态与另一个状态相连。循环的最后一个状态再次返回到初始状态。这个过程继续进行，形成一个循环。在这里，系统可能作用于周围环境（发动机周围的区域），充当热机。

卡诺循环如下图所示

卡诺循环包括以下步骤

1. 可逆等温膨胀
2. 可逆绝热膨胀
3. 可逆等温压缩
4. 等熵压缩

让我们举一个例子来描绘卡诺循环中不同阶段的功能。

在这里，我们假设有两个储热器，以及两个储热器之间带有可移动活塞的自由间隙。两个储热器是冷储热器和热储热器。活塞的膨胀和压缩将帮助我们确定气体的运动。

图如下所示

可逆等温膨胀

在此，活塞允许向上膨胀。来自热储热器的气体将流向活塞区域。在温度 T1 下，活塞从热储热器吸收的热量。

它之所以是可逆的，是因为热量从高温储热器以内容物温度可逆地传递。它之所以是等温的，是因为当气体与储热器处于热接触时，温度没有变化。

可逆绝热膨胀

在这里，气体与两个储热器都隔热。因此，没有热能的增益或损失，即绝热。气体继续膨胀，直到由于压力的降低而做功。由于气体做的内功，它会损失能量。此阶段的温度低于 T1，即 Ta。

可逆等温压缩

气体现在与低温储热器（冷）处于热接触。通过压缩活塞，环境对气体做功。这导致系统将能量 (Q2) 损失到冷储热器。它进一步降低了系统的熵。

等熵压缩

等熵是指可逆绝热过程。在这里，两个储热器也都是热绝缘的。环境对气体做功并进一步向下移动活塞。这种压缩增加了系统的内能，并且温度再次升高到 T1，即与第一阶段（可逆等温膨胀）相同的温度。系统的熵保持不变。

阶段 4（等熵压缩）现在将显示如下图像

卡诺发动机的优点

卡诺发动机的优点如下

• 根据物理定律，它被认为是最高效的热机。
• 它使用了可以有效处理的可逆过程。

卡诺发动机的缺点

卡诺发动机的缺点如下

• 根据卡诺发动机，热量在恒定温度下被吸收。现实生活中无法达到这种情况。
• 它是一个理论模型。

卡诺发动机的应用

卡诺发动机有多种应用，因为它只需要温度梯度即可执行过程。例如，蒸汽机、热机等。

数值的

让我们来看一个基于卡诺发动机的数值示例。

示例：一个热力学系统经历循环 abcda。计算如图 1 所示，在循环的不同部分由气体完成的功。还找出在整个过程中气体排出的总热量。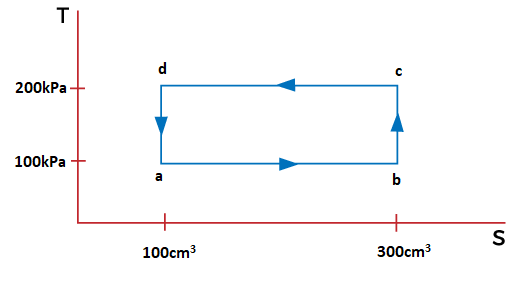

解答：我们知道上述循环在 p-V 图形形式中表示，其中 p 是以千帕为单位的压力，V 是以立方厘米为单位的体积。

在这里，我们需要找出在 ab、bc、cd 和 da 部分所做的功。

步骤 1：在 ab 部分所做的功

它由下式给出

其中，

p 是压力

V 是体积

a 代表体积 100cm³，b 代表体积 300cm³。

功 = 100kPa (300 - 100) cm³

= 100 x 1000 x 200 Pa cm³

= 20000000/1000000 Pa m³

这是因为 1 m = 100 cm

= 20 J

因此，在 ab 部分所做的功是 20 焦耳。

步骤 2：在 bc 部分所做的功

在 bc 部分状态没有变化。积分单位（体积）将相同，导致功为零。

因此，在 ab 部分所做的功是 0 焦耳。

步骤 3：在 cd 部分所做的功

它由下式给出

其中，

p 是压力

V 是体积

c 代表体积 300cm³，d 代表体积 100cm³。

功 = 200kPa (100 - 300) cm³

=- 200 x 1000 x 200 Pa cm³

= -40000000/1000000 Pa m³

这是因为 1 m = 100 cm

= -40 J

因此，在 cd 部分所做的功是 -40 焦耳。

步骤 4：在 da 部分所做的功

在 da 部分状态没有变化。积分单位（体积）将相同，导致功为零。

因此，在 cd 部分所做的功是 0 焦耳。

排出的总热量

排出的总热量等于系统在循环 abcda 期间所做的总功

= 20 J - 40 J = - 20 焦耳