连接性

• 连通性是图论的一个基本概念。它定义了一个图是连通的还是非连通的。如果没有连通性，就不可能从一个顶点到另一个顶点遍历图。
• 如果图中每对顶点之间都存在路径，则称该图为连通图。从每个顶点到任何其他顶点都必须有一些路径来遍历。 这称为图的连通性。
• 如果存在多个不连接的顶点和边，则称该图为非连通图。
• 图的连通性理论在网络应用、路由交通网络、网络容错等方面至关重要。

示例

在上面的例子中，可以从一个顶点到另一个顶点。 在这里，我们可以使用路径 B -> A -> D -> F -> E -> H 从顶点 B 遍历到 H。因此，它是一个连通图。

示例

在上面的例子中，无法从顶点 B 遍历到 H，因为它们之间没有直接或间接的路径。 因此，它是一个非连通图。

让我们看看连通性的一些基本概念。

1. 割点

移除后会断开图的单个顶点称为割点。

设 G 为连通图。 如果 G-v（从 G 中移除 v）导致图断开连接，则 G 的顶点 v 称为 G 的割点。

当我们从图中删除一个顶点时，该图将分解为两个或多个图。 该顶点称为割点。

注意：设 G 是一个有 n 个顶点的图

• 一个连通图 G 最多可能有 (n-2) 个割点。
• 删除割点可能会导致图断开连接。
• 删除顶点可能会使图中的组件数量至少增加一个。
• 树的每个非悬挂顶点都是割点。

示例 1

示例 2

在上图中，顶点“e”是割点。 从上图中删除顶点“e”后，该图将变成一个不连通的图。

2. 割边 (桥)

割边或桥是一条移除后会断开图的单条边。

设 G 为连通图。 如果 G-e（从 G 中移除 e）导致图断开连接，则 G 的边 e 称为 G 的割边。

当我们从图中删除一条边时，该图将分解为两个或多个图。 这个移除的边称为割边或桥。

注意：设 G 是一个有 n 个顶点的图

• 一个连通图 G 最多可能有 (n-1) 条割边。
• 删除割边可能会导致图断开连接。
• 删除一条边可能会使图中的组件数量最多增加一个。
• 割边“e”不能是 G 中任何循环的一部分。
• 如果存在割边，则也必须存在割点，因为割边的至少一个顶点是割点。
• 如果存在割点，则不一定存在任何割边。

示例 1

在上图中，边 (c, e) 是一条割边。 从上图中删除这条边后，该图将变成一个不连通的图。

示例 2

在上图中，边 (c, e) 是一条割边。 从上图中删除这条边后，该图将变成一个不连通的图。

3. 割集

在连通图 G 中，割集是具有以下属性的边的集合 S

• 删除 S 中的所有边会断开 G 的连接。
• 删除 S 中的一些边（但不是全部）不会断开 G 的连接。

示例 1

要断开上述图 G 的连接，我们必须删除三个边。 即 bd、be 和 ce。 我们不能仅通过删除三个边中的两个来断开它。 因此，{bd, be, ce} 是一个割集。

从上图中删除割集后，它将如下所示

4. 边连通度

连通图 G 的边连通度是移除后使 G 断开连接的最小边数。 它表示为 λ(G)。

当 λ(G) ≥ k 时，则称图 G 为 k 边连通。

示例

让我们看一个例子，

从上面的图中，通过移除两个最小的边，连通图变成不连通图。 因此，它的边连通度为 2。因此，上面的图是一个 2 边连通图。

以下是移除两条边断开图连接的四种方法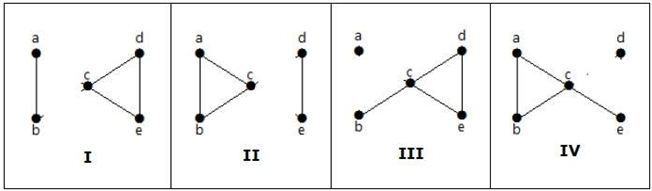

5. 顶点连通度

连通图 G 的连通度（或顶点连通度）是移除后使 G 断开连接或简化为平凡图的最小顶点数。 它表示为 K(G)。

当 K(G) ≥ k 时，该图被称为 k 连通或 k 顶点连通。 要删除顶点，我们还必须删除与其关联的边。

示例

让我们看一个例子

可以通过移除单个顶点“c”或“d”来断开上述图 G。 因此，它的顶点连通度为 1。 因此，它是一个 1 连通图。