图的表示

在图论中，图的表示是一种将图存储到计算机内存中的技术。

为了表示一个图，我们只需要顶点的集合，以及每个顶点的邻居（通过边直接连接到它的顶点）。如果它是一个加权图，则权重将与每条边相关联。

根据边的密度、要执行的操作类型和易用性，有不同的方法可以最佳地表示一个图。

1. 邻接矩阵

• 邻接矩阵是一种顺序表示方法。
• 它用于表示哪些节点彼此相邻。即，图中是否存在连接节点的边。
• 在这种表示中，我们必须构造一个 nXn 矩阵 A。如果从顶点 i 到顶点 j 有任何边，则 A 的相应元素，aⁱ,^j = 1，否则 aⁱ,^j= 0。

请注意，即使包含 100 个顶点并且只有 1 条边的图，我们仍然需要一个 100x100 的矩阵，其中包含很多零。

• 如果存在任何加权图，那么我们可以存储边的权重，而不是 1 和 0。

示例

考虑以下无向图表示

无向图表示

有向图表示

查看有向图表示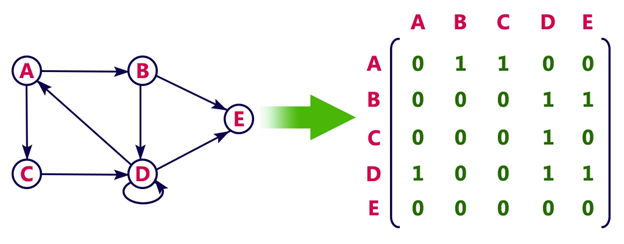

在上面的例子中，1 代表从行顶点到列顶点的边，而 0 代表从行顶点到列顶点没有边。

无向加权图表示

优点：表示更容易实现和理解。

缺点：访问顶点的所有邻居需要大量的空间和时间，我们必须遍历图中的所有顶点，这需要一些时间。

2. 关联矩阵

在关联矩阵表示中，可以使用大小为

总顶点数乘以总边数来表示图。

这意味着，如果一个图有 4 个顶点和 6 条边，那么它可以表示为 4X6 类的矩阵。在这个矩阵中，列代表边，行代表顶点。

这个矩阵填充为0或1或-1。其中，

• 0 用于表示未连接到列顶点的行边。
• 1 用于表示作为出边连接到列顶点的行边。
• -1 用于表示作为入边连接到列顶点的行边。

示例

考虑以下有向图表示。

3. 邻接表

• 邻接表是一种链接表示。
• 在这种表示中，对于图中的每个顶点，我们维护其邻居的列表。 也就是说，图的每个顶点都包含其相邻顶点的列表。
• 我们有一个顶点数组，由顶点编号索引，并且对于每个顶点 v，相应的数组元素指向 v 的邻居的单链表。

示例

让我们看看使用链表实现的以下有向图表示

我们也可以使用数组实现这种表示，如下所示

优点

• 邻接表节省了大量的空间。
• 我们可以使用链表轻松插入或删除。
• 这种表示方式易于理解，并且清晰地显示了节点的相邻节点。

缺点

• 邻接表允许测试两个顶点是否彼此相邻，但它支持此操作的速度较慢。