图的类型

虽然根据顶点数、边数、互连性和整体结构，有很多不同类型的图，但一些常见的图类型如下：

1. 空图

空图是指顶点之间没有边的图。空图也称为空图。

示例

具有 n 个顶点的空图表示为 Nn。

2. 平凡图

平凡图是指只有一个顶点的图。

示例

在上面的图中，只有一个顶点“v”，没有任何边。因此，它是一个平凡图。

3. 简单图

简单图是没有平行边和自环的无向图。

示例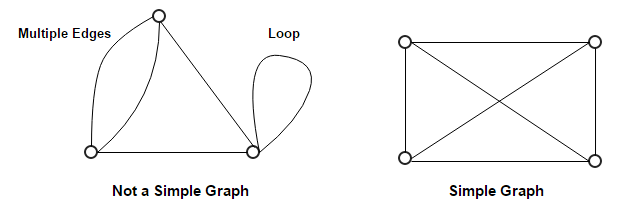

在上面的例子中，第一个图不是简单图，因为它在顶点 A 和 B 之间有两条边，并且它也有一个自环。

第二个图是一个简单图，因为它不包含任何自环和平行边。

4. 无向图

无向图是指边没有方向的图。

示例

在上面的图中，由于没有有向边，因此它是一个无向图。

5. 有向图

有向图是指边用箭头指示方向的图。

有向图也称为 digraphs。

示例

在上面的图中，每条边都用箭头指示方向。从 A 到 B 的有向边表示 A 与 B 相关，但 B 与 A 不相关。

6. 完全图

图中每对顶点都恰好由一条边连接，则称为完全图。 它包含所有可能的边。

具有 n 个顶点的完全图恰好包含 nC2 条边，并表示为 Kn。

示例

在上面的示例中，由于图中的每个顶点都通过恰好一条边与所有剩余顶点相连，因此这两个图都是完全图。

7. 连通图

连通图是指我们可以从任何一个顶点访问到任何其他顶点的图。 在连通图中，每对顶点之间至少存在一条边或路径。

示例

在上面的例子中，我们可以从任何一个顶点遍历到任何其他顶点。 这意味着每对顶点之间至少存在一条路径，因此，它是一个连通图。

8. 非连通图

非连通图是指每对顶点之间不存在任何路径的图。

示例

上面的图由两个独立的组件组成，它们是不连通的。 由于不可能从一个组件的顶点访问到另一个组件的顶点，因此它是一个非连通图。

9. 正则图

正则图是指所有顶点的度都相同的图。

如果所有顶点的度为 k，则称为 k-正则图。

示例

在上面的例子中，所有顶点的度都为 2。因此，它们被称为 2-正则图。

10. 循环图

具有“n”个顶点（其中 n>=3）和“n”条边，形成一个边数为“n”的环的图称为循环图。

图中包含至少一个循环，则称为循环图。

在循环图中，每个顶点的度为 2。

具有 n 个顶点的循环图表示为 Cn。

示例 1

在上面的例子中，所有顶点的度都为 2。因此它们都是循环图。

示例 2

由于上面的图包含两个循环，因此它是一个循环图。

11. 无环图

不包含任何循环的图称为无环图。

示例

由于上面的图不包含任何循环，因此它是一个无环图。

12. 二分图

二分图是指顶点集可以划分为两个集合的图，使得边仅在集合之间连接，而不是在集合内部连接。

如果图 G (V, E) 的顶点集 V(G) 可以分解为两个非空不相交的子集 V1(G) 和 V2(G)，使得每个边 e ∈ E(G) 在 V1(G) 中都有其一个终点，在 V2(G) 中有另一个终点，则称图 G (V, E) 为二分图。

划分 V = V1 ∪ V2 被称为 G 的二分划分。

示例 1

示例 2

13. 完全二分图

完全二分图是指第一个集合中的每个顶点都恰好通过一条边连接到第二个集合中的每个顶点的二分图。

完全二分图是完整的二分图。

示例

上面的图称为 K₄,₃。

14. 星形图

星形图是完全二分图，其中 n-1 个顶点的度为 1，单个顶点的度为 (n -1)。 这看起来完全像一颗星，其中 (n - 1) 个顶点连接到单个中心顶点。

具有 n 个顶点的星形图表示为 S_n。

示例

在上面的例子中，在 n 个顶点中，所有 (n-1) 个顶点都连接到单个顶点。 因此，它是一个星形图。

15 加权图

加权图是指边被标记了一些权重或数字的图。

加权图中路径的长度是路径中所有边的权重之和。

示例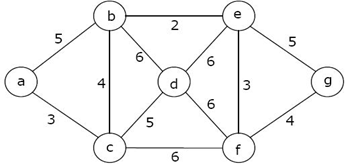

在上面的图中，如果路径是 a -> b -> c -> d -> e -> g，则路径的长度是 5 + 4 + 5 + 6 + 5 = 25。

16. 多重图

任何一对顶点之间有多条边或从顶点到自身（环）存在边的图称为多重图。

示例

在上面的图中，顶点集 B 和 C 由两条边连接。 类似地，顶点集 E 和 F 由 3 条边连接。 因此，它是一个多重图。

17. 平面图

平面图是指我们可以将其绘制在一个平面上，使得它的任何两条边都不会相互交叉，除非在它们相交的顶点处。

示例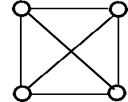

上面的图可能看起来不是平面的，因为它有相互交叉的边。 但是我们可以重绘上面的图。

上面图的三个平面图是

上面的三个图不包含相互交叉的边，因此，上面的所有图都是平面的。

18. 非平面图

不是平面图的图称为非平面图。 换句话说，无法绘制且至少有一对边交叉的图称为非平面图。

示例

上面的图是一个非平面图。