树和森林

1. 什么是树和森林？

Tree

• 在图论中，一棵树是一个无向、连通且无环的图。 换句话说，一个不包含任何环的连通图称为树。
• 树以图形形式表示层次结构。
• 树的元素称为节点，树的边称为分支。
• 一棵具有 n 个顶点的树有 (n-1) 条边。
• 树提供了许多有用的应用程序，从简单的家谱到计算机科学的数据结构中的树，复杂多样。
• 树中的叶子是度为 1 的顶点，或没有任何子节点的任何顶点都称为叶子。

示例

在上面的例子中，所有树的顶点数都少于 6 个。

森林

在图论中，森林是一个无向、不连通且无环的图。换句话说，树的互不相交的集合称为森林。森林的每个组成部分都是一棵树。

示例

上图看起来像两个子图，但它是一个不连通的图。上图中没有循环。因此它是一片森林。

2. 树的属性

1. 每个至少有两个顶点的树应该至少有两个叶子。
2. 树有许多特征
   设 T 是一个具有 n 个顶点的图，则以下语句是等效的
   • T 是一棵树。
   • T 不包含环，并且有 n-1 条边。
   • T 是连通的，并且有 (n -1) 条边。
   • T 是连通图，并且每条边都是割边。
   • 图 T 的任意两个顶点都恰好由一条路径连接。
   • T 不包含环，并且对于任何新边 e，图 T+ e 恰好有一个环。
3. 树的每条边都是割边。
4. 向树添加一条边定义了恰好一个环。
5. 每个连通图都包含一个生成树。
6. 每棵树至少有两个度为二的顶点。

3. 生成树

在连通图 G 中，生成树是 G 的一个子图 H，它包括 G 的所有顶点，也是一棵树。

示例

考虑以下图 G

从上图 G 中，我们可以实现以下三个生成树 H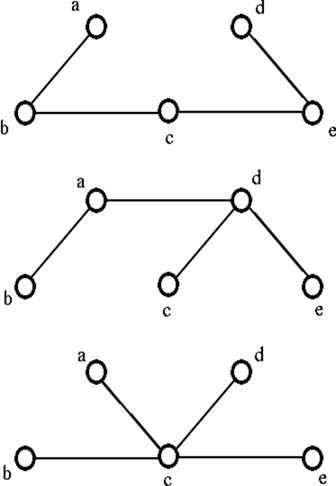

查找生成树的方法

我们可以使用两种方法中的任何一种系统地找到生成树

1. 切割法
2. 构建法

1. 裁剪法

• 首先选择图 G 中的任何一个环。
• 删除环的其中一条边。
• 重复此过程，直到没有剩余循环。

示例

• 考虑图 G，

• 如果我们在上图中删除边 ac，它会破坏环 a-d-c-a，那么我们得到以下图

• 删除边 cb，它破坏了上图中的环 a-d-c-b-a，然后我们得到以下图

• 如果删除边 ec，它会破坏上图中的环 d-e-c-d，那么我们得到以下生成树

2. 构建法

• 一次选择图 G 的边。 这样就不会创建循环。
• 重复此过程，直到包含所有顶点。

示例

考虑以下图 G，

• 选择边 ab，

• 选择边 de，

• 之后，选择边 ec，

• 接下来，选择边 cb，最后我们得到以下生成树

电路秩

我们需要从 G 中删除的边数才能得到生成树。

生成树 G = m- (n-1)，这称为 G 的电路秩。

示例

在上图中，边 m = 7，顶点 n = 5

那么电路秩是，