数字信号处理多选题

答案: (b) 偶

描述: 令 x1(n) 和 x2(n) 为两个信号。

如果这两个信号都是奇函数，则 x1(-n) = - x1(n) 且 x2(-n) = - x2(n)

如果一个信号是偶函数，则 x(-n) = x(n)

x(-n) = x1(-n) . x2(-n)

x(-n) = - x1(n). - x2(n)

x(-n) = x1(n). x2(n)

这意味着 x(-n) = x(n)，这是偶函数。

因此，两个奇信号的乘积是偶函数。

答案: (b) 因果的

描述

步骤 1: 如果系统的输出仅取决于过去和现在的输入，则该系统是因果的。我们来检查它的因果性。

我们将检查 y(n) 对不同 n 值的计算。

对于,

n= 0, y(0) = x(0) + 1/x(-1)

n = 1, y(1) = x(1) + 1/x(0)

因此，该系统是因果的。

步骤 2: 满足叠加定理的系统可以归类为线性系统。

Y1(n) = x1(n) + 1/x1(n - 1)

Y2(n) = x2(n) + 1/x2(n - 1)

要满足线性，ay1(n) + by2(n) = ax1(n) + bx2(n)

左边

ay1(n) + by2(n) = a [x1(n) + 1/x1(n - 1)] + b [x2(n) + 1/x2(n - 1)]

ay1(n) + by2(n) = ax1(n) + bx2(n) + a/x1(n - 1) + b/x2(n - 1)

它不等于 RHS

因此，该系统是非线性的。

答案: (d) 非动态系统

描述: 系统可以分为静态、动态、因果、非因果、递归、非递归等。非动态不是离散系统的一种类型。

答案：(d) 以上均正确

描述: DSP 的优点是成本低、分时能力强、灵活性高。

答案: (a) 功率信号是无限的。

描述: 功率信号是无限的，因为它存在于无限持续时间内。因此，它不是时限的。周期信号是功率信号，而非周期信号是能量信号。

答案： (d) (a) 和 (c) 都对

描述: 模拟数字处理不适用于低频信号。数字信号处理消耗更多功率，并且适用于低频信号。

答案: (b) n = n1 + n2 - 1

描述: 计算两个信号序列长度的公式是 n = n1 + n2 - 1。例如，

如果 n1 = 4 且 n2 = 3，则 n = 4 + 3 - 1 = 6

答案: (b) 0.04s

描述: 已知，带宽 = 5 KHz。

N = 2^m，其中 m 是整数

信号的最小长度 (T) 由下式给出

T = L/Fs

其中，

L 是所需样本的最小数量

Fs 是最小采样率

Fs = 2fm

这意味着采样率是带宽的两倍。

Fs = 2 x 5 = 10 KHz。

L = Fs/Resolution

所以，T = (Fs/ Resolution)/ Fs

T = 1/Fs

T = 1/25Hz

T = 0.04s

答案: (a) 单边 Z 变换

描述: 双边 Z 变换称为双边变换。单边称为单边 Z 变换。

答案: (c) z/ z - 1

描述: 给定信号: y(n) = x(n) + y(n - 1)

对两边应用 Z 变换，

Z [y(n)] = Z [x(n)] + Z y[(n - 1)]

Y(z) = X(z) + z^(-1) Y(z)

Y(z) - z^(-1) Y(z) = X(z)

Y(z) (1 - 1/z) = X(z)

Y(z) (1 - 1/z) = X(z)

Y(z)/X(z) = 1/ (1 - 1/z)

H(z) = z / z-1

因此，函数 y(n) = x(n) + y(n - 1) 的 Z 变换是 z / z-1，即选项 (c)。

答案: (b) X(z/a)

描述: 上述属性定义为信号的比例属性。信号 a^nx(n) 的 Z 变换是 X(z/a)。

答案: (a) 1 + 2z^- 1

描述: n 序列的 Z 变换由下式给出

Z [y(n)] = Z [x(n)] + Z [2x(n - 1)]

Y(z) = X(z) + 2z^-1X(z)

Y(z) = X(z) (1 + 2z^-1)

Y(z)/X(z) = 1 + 2z^-1

H(z) = 1 + 2z^-1

答案: (c) 零填充

描述: 零填充通常用于循环卷积，如果两个给定序列的长度不相等。

答案: (d) z/ z - 3

描述: Z 变换由下式给出

所以，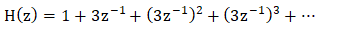

H(z) = 1/(1 - 3/z)

H(z) = z/ z - 3

因此，系统 h(n) = 3^n u(n) 的 Z 变换是 z/ z - 3。

答案: (b) 离散时间系统

描述: 离散时间系统接受输入并以离散形式产生输出。

答案: (a) 36

描述: 令两个序列为 M 和 N。

M = 40

N = 900

DFT 数量 = 64

所需的较小 DTS 数量 = L + M - 1 = 给定的 DFT 点数

L + M - 1 = 64

L + 40 - 1 = 64

L = 25

总块数 = N / L = 900/25 = 36

因此，计算线性卷积所需的最小 DFT 数量是 36。

答案: (c) 992

描述: 复数加法的数量由 N (N - 1) 给出。

其中，

N 是直接 DFT 计算的次数

这里，N 是 32。

所以，复数加法 = 32 (32 - 1)

= 32 x 31

= 992

答案: (a) 256

描述: 复数乘法由 N^2 给出。

其中，

N 是直接 DFT 计算的次数

这里，N 是 16。

所以，复数乘法 = 16 x 16 = 256。

答案: (d) 输出序列以位反转顺序表示。

描述: DIT-FFT 的输出序列以常规顺序而不是位反转顺序表示。

答案: (c) 1 和 4

描述: 线性卷积不需要使用零填充。输出序列的长度大于输入序列的长度。

答案: (b) {0.5, 0, 0.5, 0}

描述: IDFT 由下式给出

x(n) = IDFT [X(k)]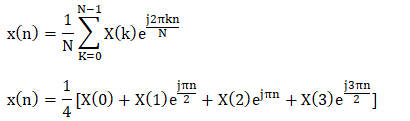

步骤 1: 对于 n = 0

x(0) = ¼ [ x(0) + x(1) + x(2) + x(3)]

= ¼[1 + 0 + 1 + 0]

= 2/4

= 1/2

= 0.5

步骤 2: 对于 n = 1

x(1) = ¼ [ x(0) + x(1) + x(2) + x(3)]

= ¼[1 + 0(j)+ 1(-1) + 0(-j)]

= ¼ [1 +0 -1 + 0]

= 0

步骤 3: 对于 n = 2

x(2) = ¼ [ x(0) + x(1) + x(2) + x(3)]

= ¼[1 + 0(-1)+ 1(1) + 0(-1)]

= ¼[1 + 0 + 1 + 0]

= 2/4

= 1/2

= 0.5

步骤 4: 对于 n = 3

x(3) = ¼ [ x(0) + x(1) + x(2) + x(3)]

= ¼[1 + 0(-j)+ 1(-1) + 0(j)]

= ¼ [1 +0 - 1 + 0]

= 0

因此，x(n) = {0.5, 0, 0.5, 0}

答案: (c) 分治法。

描述: 分治法是一种高效的算法，用于基于 N 点 DFT 分解来计算 DFT。

答案: (d) N (M + L - 2)

描述: 复数加法由 N (M + L -2) 给出。

其中，

M 和 L 是给定数据数组的整数，N 是点 DFT 的数量。

上述方法的复数加法次数少于直接形式的方法。

答案: (b) 12

描述: 复数乘法的数量由以下公式给出: N/2(log2N)

其中，

N 是点 DFT。

因此，复数乘法 = 8/2 (log2 8)

= 4 x 3 = 12。

答案：(d) 以上均正确

描述: 蝶形结构是一种高效的结构，具有多种优点，例如降低复杂性、减少乘法和加法。它还将小 DFT 的结果合并到大 DFT 中，反之亦然。

答案: (c) 级联中的滤波器以并行方式连接。

描述: 级联实现中的滤波器以串联方式连接。

答案: (a) 当系统的相位响应随频率函数线性变化时。

描述: 正如其名称所示，系统的相位响应随频率线性变化。

答案: (c) 仅 3

描述: FIR 滤波器通常是规范滤波器。非规范滤波器是 IIR 滤波器。

答案: (c) 可编程。

描述: 数字滤波器是可编程的、成本较低的，并且功耗较高。它可以轻松处理低频信号。

数字滤波器的操作由存储在处理器内存中的程序决定。因此，这些滤波器通常是可编程的。

答案: (a) 脉冲不变法

描述: 实际的模拟滤波器通常不是完全带限的。因此，使用脉冲不变法的滤波器可能会在滤波器中引起这种混叠效应。

答案: (d) (a) 和 (b)。

描述: 处理器的片上寄存器可以存储中间结果。因此，选项 (c) 不正确。

答案: (b) 3/4 y(n - 1) - 1/8 y(n - 2) + x(n) + 1/3x(n - 1)

描述: 直接型-I 是在找到图两边的 X(z) 和 Y(z) 的 Z 变换后形成的结构。让我们首先确定 X(z) 和 Y(z)，然后进行它们的逆 Z 变换以找到离散系统的方程。

步骤 1: LHS

左侧是 X(z)。

X(z) [1 + 1/3 z^-1] = W(z)

X(Z) + 1/3 z^-1 X(z) = W(z)

逆可以表示为

x(n) + 1/3x(n - 1) = w(n)

步骤 2: RHS

右侧是 Y(z)。

Y(z) = 3/4 z^-1 Y(z) - 1/8 z^-2 Y(z) + W(z)

逆可以表示为

y(n) = 3/4 y(n - 1) - 1/8 y(n - 2) + w(n)

将步骤 1 中 w(n) 的值代入，我们得到

y(n) = 3/4 y(n - 1) - 1/8 y(n - 2) + x(n) + 1/3x(n - 1)

这是给定系统的离散方程。

答案: (d) (a) 和 (b)

描述: 两条总线程序存储器总线和数据存储器总线提供了额外的处理器接口。

答案: (a) 直接型- I

描述: 直接型有两种形式，直接型 I 和直接型 II。这两种形式都可用于 IIR（无限冲激响应）滤波器。

答案: (b) 一阶系统。

描述: 上图仅显示了一个 z^-1 的值，这表明该系统是一阶的。

答案: (c) M + N - 1

描述: IIR 滤波器的乘法器由下式给出

M + N - 1

答案: (a) 17

描述: 给定，

N = 1024

M = 100

L = N - M + 1 = 1024 - 100 + 1 = 925

处理数据块的数量 = 输入样本/925 = 16000/925 = 17.29 ≈ 17

答案: (d) FIR 滤波器不受噪声影响。

描述: FIR 滤波器对噪声具有高度免疫力。

答案: (d) 窗频谱的旁瓣幅度保持不变。

描述: 主瓣宽度是矩形窗的两倍。所需的最小阻带衰减约为 31 dB。

答案： (d) 以上都不是

描述: 关于窗函数技术的所有陈述都是正确的。

答案: (b) 布莱克曼窗

描述: 布莱克曼窗的主瓣宽度大于所有其他窗技术，等于 12pi/N。

答案: (a) I 型切比雪夫滤波器

描述: II 型切比雪夫滤波器同时包含极点和零点。因此，I 型切比雪夫滤波器是全极点滤波器。

答案: (b) 2 和 3

描述: 巴特沃斯滤波器的极点位于圆上，而不是椭圆上。切比雪夫滤波器的幅度响应在通带内有纹波，而不是巴特沃斯滤波器。

答案: (c) 缺乏多对一映射。

描述: 多对一映射的存在是脉冲不变法的一个主要缺点。这意味着 s 平面上的多个点映射到 z 平面上的一个点。它还可能在滤波器中引起混叠效应。

答案: (a) Fs = 2 Fm

描述: 奈奎斯特采样率是最大频率的两倍。

答案：(d) 以上均正确

描述: 标准测试信号分为阶跃、冲激、指数、斜坡、正弦等。因此，所有三个选项都是正确的。