控制系统 MCQ2025年3月17日 | 阅读 24 分钟 1) 自动控制理论的主要部分适用于
答案: (b) 线性时不变系统 解释: 线性时不变 (LTI) 系统无论何时输入,对于相同的输入都会产生相同的输出。LTI 系统也用于预测系统的长期行为。 因此,正确答案是选项 (b)。 2) 红绿灯系统是...的例子
答案: (a) 开环系统 解释: 交通信号灯将根据设定的时间和顺序亮起,并且依赖于时间。顺序和时间由继电器控制,继电器基于预设程序工作。它不依赖于道路上的车流量。 因此,正确答案是选项 (a)。 3) 如下阶跃函数所示的拉普拉斯变换是 
答案: (d) 1/s 解释: 阶跃函数的输入突变发生在 t=0 时,且阶跃大小为 1 个单位。 设阶跃函数的大小为 A,其中 A=1。 函数 f(t) 的拉普拉斯变换由下式给出 L[f(t)] = F(s) = ∫0∞f(t) e-st dt F(s) = ∫0∞Af(t) e-st dt F(s) = -A/s (e-∞-e-0) F(s) = A/s 我们知道,A =1 F(s) = 1/s 因此,正确答案是选项 (d)。 4) 负反馈闭环系统受到 15V 电压。系统的前向增益为 2,反馈增益为 0.5。确定输出电压和误差电压。
答案: (c) 15V, 7.5V 说明 给定 G(s) = 2 H(s) = 0.5 and R(s) = 10V 输出电压: = (2/1+2x 0.5) x 15 = 15V 误差电压: = (1/1+2x 0.5) x 15 = 7.5V 因此,正确答案是选项 (c)。 5) 静态系统可定义为
答案: (d) 系统的输出仅取决于当前输入 解释: 静态系统没有任何反馈系统。因此,输出仅取决于当前输入。 因此,正确答案是选项 (d)。 6) 求以下函数 F(s) 的函数 f(t) 
答案: (b) -0.2-0.25e-t+0.05e-5t 解释: 给定函数可以写成
1 = A(s+1)(s+5) +Bs(s+5) +Cs(s+1) 要计算 A 的值,将 s= 0 代入,得到 1 = A(1)(5) A = 1/5 = 0.2 现在,要计算 B 的值,将 s=-1 代入,得到 1 = B (-1)(4) B = -1/4 = -0.25 类似地,将 s=-5 代入,得到 1 = C (-5) (-4) C = 1/20 = 0.05 将 A、B 和 C 的值代入 F(s),得到 F(s) = A/s + B/ (s+1) + C/(s+5) F(s) = 0.2/s - 0.25/ (s+1) + 0.05/(s+5) 我们知道,1/(s + a) 的拉普拉斯变换是 e-at,1/s = 1。 f(t) = -0.2-0.25e-t+0.05e-5t 因此,正确答案是选项 (b)。 7) 给定系统的力方程是   答案: 说明 给定:x 是上面图中的位移。x 的拉普拉斯变换是 X(s)。控制系统的微分方程是这些节点的平衡力方程。 此处, F 是质量引起的反作用力。 F = f 是摩擦引起的反作用力 F = k 是理想弹性弹簧元件,它具有可忽略的质量和摩擦。弹簧产生的力与身体的位移成正比。 F = Kx 因此,力方程可以表示为  因此,正确答案是选项 (c)。 8) 求给定系统的传递函数 
答案: (a) 解释: 我们将首先将 H1 块移到 G3 之后 移走取样点将使块成为:H1/ G3 块 G2 和 G3 是串联的。等效块将是这两个块的乘积 (G2G3)。 该块的增益将是 G2G3/ (1 + H2G2G3) 如所示,G1 是串联的,以上系统的传递函数将是 C(s)/R(s) = [G1G2G3/ (1 + H2G2G3)]/ [1 + G1G2G3/ (1 + H2G2G3) x H1/G3 C(s)/R(s) = G1G2G3/ (1 + H2G2G3 + G2G1H1) 因此,正确答案是选项 (a)。 9) 环路增益等于
答案: (b) 遍历前向路径时所有支路增益的乘积 解释: 根据梅森增益公式,传递函数可以计算为 T(s) = C(s)/R(s)  其中, Pk 是前向路径增益 ∆ 是环路增益,计算方法如下 ∆=1-∑(所有环路增益) + ∑(两个不相交环路的增益乘积)-∑(三个不相交环路的增益乘积) ∆k 通过消除所有与 Pk 相交的环路来计算 此处,环路增益定义为遍历前向路径的支路增益的乘积。 因此,正确答案是选项 (b)。 梅森增益公式用于计算信号流图的整体传递函数。 10) 求给定信号流图的整体传递函数。 
答案: (a) G1G2G3/ (1 + G1H1 + G3H2 + G3G1H1H2) 解释: 这里,我们将使用梅森增益公式计算传递函数  其中, Pk 是前向路径增益 ∆ 是环路增益,计算方法如下 ∆=1-∑(所有环路增益) + ∑(两个不相交环路的增益乘积)-∑(三个不相交环路的增益乘积) ∆k 通过消除所有与 Pk 相交的环路来计算 现在, 步骤 1: 从图中,我们识别前向路径, P1 = G1G2G3 图中只有一个前向路径。 步骤 2: 现在,我们来找环路增益。有两个环路 L1 = -G1H1 L2 = -G3H2 步骤 3: 两个不相交的环路。只有一个两个不相交环路的组合,如下所示  L1 L2 = G3G1H1H2 步骤 4: 由于没有三个不相交的环路,我们将直接计算系统的行列式。 ∆= 1 - (L1+ L2) + (L1L2) = 1 + G1H1 + G3H2 + G3G1H1H2 步骤 5: 这里,我们将计算 ∆1,因为只有一个前向路径。 对于 ∆1,我们将消除 L1 和 L2,因为两个环路增益都与前向路径相交。 L1 = L2 = 0 ∆1=1-0=1 现在,传递函数为:C/R = G1G2G3/ (1 + G1H1 + G3H2 + G3G1H1H2) 因此,正确答案是选项 (a)。 11) 闭环系统的框图表示。假设初始条件为零,写出具有单位阶跃输入的系统的瞬态响应方程。
答案: (c) 1-e-t⁄10 说明 环路的传递函数为 G/ (1+GH) 我们首先将以上框图简化为简单系统。我们来计算第一个环路的传递函数。 TF = [1/ (40s+2)] / [1 + 2/ (40s+2)] = 1/ (40s +4) 现在,剩下两个串联的块。等效块是这两个块的乘积,如下所示 C(s)/R(s) = 4. (1/ (40s +4)) = 1/ (10s + 1) 阶跃输入的拉普拉斯变换是 1/s。这意味着 R(s) = 1/s。 C(s) = [1/ (10s + 1)]. R(s) C(s) = [1/ s (10s + 1) 对上述方程进行拉普拉斯逆变换,得到 1-e-t⁄10 12) 如果闭环系统的特征方程是 s^2 + 2s + 2 = 0,则该系统是
答案: (d) 欠阻尼 解释: 给定方程是:s^2 + 2s + 2 = 0 这是一个二阶微分方程。标准形式二阶微分方程的拉普拉斯变换是  因此,该系统是欠阻尼的。 因此,正确答案是选项 (d)。 13) 系统的传递函数为 81/ (s^2 + 16s + 81)。求单位阶跃输入的无阻尼自然频率、阻尼比和峰值时间。
答案: (a) 9, 0.889, 0.762 解释: 标准传递函数可以写成  给定方程是:81/ (s^2 + 16s + 81) 比较值,得到 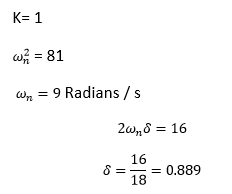 因此,无阻尼自然频率为 9,阻尼比为 0.889。 峰值时间可以计算为  因此,正确答案是选项 (a)。 14) 二阶系统的闭环传递函数为:T(s) = 4/ (s^2 + 4s + 4)。计算 2% 和 5% 带宽的稳定时间。
答案: (c) 2.0, 1.5 解释: 标准传递函数可以写成  给定方程是:4/ (s^2 + 4s + 4) 比较值,得到 K= 1  2% 带宽的稳定时间计算如下  稳定时间 = 2 秒 5% 带宽的稳定时间计算如下  稳定时间 = 1.5 秒 因此,正确答案是选项 (c)。 15) 考虑一个传递函数为 G(s) = (s + 4)/ (ks^2 + s + 4) 的系统。当 k 的值为...时,阻尼比为 0.5
答案: (b) ¼ 解释: 给定的传递函数是 G(s) = (s + 4)/ (ks^2 + s + 4) 特征方程 ks^2 + s + 4 = 0 将方程除以 k,得到 S^2 +s/k + 4/k = 0  因此,正确答案是选项 (b)。 16) 具有单位反馈的系统 G(s) = 1/ (s+2)(s+3) 的阶跃误差系数是
答案: (d) 1/6 解释: 阶跃误差可以计算为 ess = sR(s)/ (1 + G(s)) R(s) = 1/s (在单位反馈的情况下) G(s) = 1/ (s+2)(s+3) ess = (s x 1/s )/ (1 + (1/ (s+2)(s+3))) ess = 1/(1 + kp) 其中,kp 是阶跃误差系数 Kp 可以计算为  因此,正确答案是选项 (d)。 17) 控制系统的传递函数为 G(s) = 25/ (s^2 + 6s + 25)。响应的第一个最大值发生在 t,其值为
答案: (c) π⁄4 解释: 给定的传递函数是:G(s) = 25/ (s^2 + 6s + 25) 将给定传递函数的值与标准方程进行比较  因此,正确答案是选项 (c)。 18) RL 电路的冲激响应是
答案: (d) 指数衰减函数 解释: RL 电路由串联的电阻和电感组成。 方程可以写成 1 = RI(s) + sLI(s) 1 = I(s) [R + sL] I(s) = 1 / (R +sL) 进行拉普拉斯逆变换,得到  方程清楚地表明冲激响应是指数衰减函数。 因此,正确答案是选项 (d)。 19) 计算给定传递函数 G(s) = 5 (s + 2)/ (s^2 + 3s + 2) 的极点和零点
答案: (a) -2, (-1, -2) 解释: 通过使分子等于零来计算零点 5 (s + 2) = 0 5s + 10 = 0 5s = -10 s = -2 通过使分母等于零来计算极点 s^2 + 3s + 2 = 0 s^2 + 2s + s + 2 = 0 s (s + 2) + 1 (s + 2) = 0 (s + 1) (s + 2) = 0 s = -1, -2 因此,正确答案是选项 (a)。 20) 给定方程 s^3 + 3s^2 + 4s + 1 = 0 在 s 平面的左半部分有多少个根
答案: (b) 三个 解释: 给定的特征方程是:s^3 + 3s^2 + 4s + 1 = 0。 为了找到根的数量,我们需要创建一个劳斯表,如下所示  如上表所示,RHS 平面没有根且没有显著变化。因此,所有三个根都位于 LHS 平面。 因此,正确答案是选项 (b)。 21) 具有多项式 s^4 + 5s^3 + 3s^2 + 6s + 5 = 0 的系统是
答案: (a) 不稳定 解释: 给定的特征方程是:s^4 + 5s^3 + 3s^2 + 6s + 5 = 0。我们首先需要通过创建劳斯阵列表来找到根。 劳斯阵列表如下所示  上表的第一个列中有两个符号变化。这意味着有两个根位于 RHS 平面。因此,系统不稳定。 因此,正确答案是选项 (a)。 22) 如果 s^3 + Ks^2 + 5s + 10 = 0,则反馈系统特征方程的根称为临界稳定。那么,K 的值将是
答案: (b) 2 解释: 对于以上方程,我们需要通过创建劳斯阵列表来找到根。给定方程是:s^3 + Ks^2 + 5s + 10 表格如下  为了使系统临界稳定,我们将 (5K -10)/K = 0 5K - 10 = 0 5K = 10 K = 2 系统称为临界稳定的 K 值为 2。 因此,正确答案是选项 (b)。 23) 如果 s^3 + 3s^2 + 4s + A = 0,特征方程的根位于 s 平面的左半部分。A 的值称为
答案: (a) 0 < A < 12 解释: 对于以上方程,我们需要通过创建劳斯阵列表来找到根。给定方程是:s^3 + 3s^2 + 4s + A = 0 表格如下  劳斯表的第一个列中没有符号变化。这意味着所有根都位于 s 平面的左半部分。 代入 A 和 (12 - A)/3 > 0,我们得到 A > 0 (或 0 < A) (12 - A)/3 > 0 12 - A > 0 12 > A (或 A < 12) 从以上方程,我们得到 A 的两个值,即 A > 0 和 A < 12。这意味着 A 位于 0 和 12 之间,如下所示 0 < A < 12 因此,正确答案是选项 (a)。 24) 对于给定的闭环系统,稳定性 K 值的范围是 
答案: (c) -19.5 < k < 8 解释: 上图中的两个块是串联的。因此,等效块将是这两个块的乘积。 G(s) = k (s - 2) /(s +1) (s^2 + 9s + 16) 现在,H(s) = 1,如上框图所示。特征方程将是:1 + G(s) H(s) C(s) = 1 + [k (s - 2) / (s + 1) (s^2 + 9s + 16)] = 0 = s^3 + 10s^2 + 25s + 16 + ks - 2k = s^3 + 10s^2 + s (25 + k) + 16 - 2k 对于以上方程,我们需要通过创建劳斯阵列表来找到根。 表格如下  为了稳定, 16 - 2k > 0 16 > 2k 8 > k 或 k < 8 10 (25 + k) - (16 -2k) /10 > 0 250 + 10k -16 + 2k > 0 12k + 234 > 0 12k > -234 k > -19.5 从 k 的两个值,我们可以说它介于 -19.5 < k < 8 之间 因此,正确答案是选项 (c)。 25) 求单位反馈系统 G(s) = ((s + 2) (s+3) (s + 4)) / ((s + 5) (s+6) (s + 1)) 的开环传递函数的渐近线数量 G(s) = ((s + 2) (s+3) (s + 4)) / ((s + 5) (s+6) (s + 1))
答案:(b) 0 解释: 系统中渐近线的数量等于趋于无穷的分支数量。所以,计算渐近线数量的公式是 P -Z。这里,P 和 Z 分别代表极点和零点。 我们知道通过使分母和分子等于零来计算极点和零点。所以,对于给定的开环传递函数,我们得到 P = 3 Z = 3 所以,无穷远处的零点数量 = 3 - 3 = 0 因此,正确答案是选项 (b)。 26) 开环传递函数为 G(s) = K (s + 1) / (s + 4)(s^2 + 3s + 2)。它具有
答案: (c) 两个无穷远处的零点 解释: 计算无穷远处零点数量的公式是 P - Z。这里,P 和 Z 是给定传递函数中的极点和零点数量。 我们知道通过使分子等于零来计算零点,通过使分母等于零来计算极点。所以,对于上面给定的传递函数,我们得到 P = 3 Z = 1 所以,无穷远处的零点数量 = 3 - 1 = 2 因此,正确答案是选项 (c)。 27) 根轨迹中的质心是一个点,在那个点
答案: (c) 渐近线穿过实轴。 解释: 质心定义为所有渐近线在实轴上相交的公共点。质心值始终是实数。但是,它可以位于正实轴或负实轴上。 28) 计算给定系统的质心 G(s) = K / [(s + 1) (s + 4 + 4j) (s + 4 - 4j)]
答案: (d) -3 说明 我们将首先计算趋于无穷的分支数量,然后计算渐近线。借助渐近线,我们将计算质心值。 系统的给定传递函数是 G(s) = K / [(s + 1) (s + 4 + 4j) (s + 4 - 4j)]。 渐近线的数量等于趋于无穷的分支数量。没有零点,但有三个极点。 所以,P - Z = 3 让我们通过使分母等于零来计算极点值。我们得到 极点位于:-1, 渐近线的角度由下式计算 Θ = (2q + 1) 180 / (P - Z) 这里,q = 0, 1, 2… 渐近线的数量等于趋于无穷的分支数量。 所以,我们将计算 q 值为 0、1 和 2 时的渐近线。 对于 q = 0, Θ=180⁄3=60度 对于 q = 1, Θ=(2+1) 180⁄3=180度 当 q = 2 时, Θ=(4+1) 180⁄3=300度 质心定义为所有渐近线在实轴上相交的公共点。 σ= / (P - Z) σ= (- 1 - 4 - 4 - 0) / 3 σ=(-9)⁄3 σ=-3 因此,正确答案是选项 (d)。 29) 反馈控制系统的特征方程给出为:s^3 + 4s^2 + (K + 5)s + K = 0 这里,K 是一个可缩放的变量参数。在系统的根轨迹图中,当 K 值较大时,根轨迹的渐近线在 s 平面上的交点坐标为
答案: (b) (-2, 0) 说明 反馈控制系统的给定方程是 s^3 + 5s^2 + (K + 6)s + K = 0。 以上方程也可以写成 s^3 + 5s^2 + Ks + 6s + K = 0 s^3 + 5s^2 + 6s + K(s + 1) = 0 s (s^2 + 5s + 6) + K(s + 1) = 0 1 + K(s + 1) / [s (s^2 + 5s + 6)] = 0 1 + K(s + 1) / s (s^2 + 2s + 3s + 6) = 0 1 + K(s + 1) / s (s + 2)(s + 3) = 0 现在,我们将计算质心值,它等于 σ= / (P - Z) 这里,极点和零点的数量分别为 3 和 1。 σ= [(0 - 2 - 3) + 1] / (3 - 1) σ=(-4)⁄2 σ=-2 因此,正确答案是选项 (b)。 30) 在单位反馈控制系统的波特图中,增益交叉频率处的 G(jw) 的相位值为 -115 度。系统的相位裕度是
答案: (d) 65 度 解释: 相位裕度可以计算为 180 + 其中, ∅ 是增益交叉频率处的 G(jw) 的相位。 所以,相位裕度 = 180 + (-115) = 180 - 115 = 65 度 因此,正确答案是选项 (d)。 31) 二阶系统的增益裕度是
答案: (b) 无穷大 解释: 增益裕度表示在不影响系统稳定性时系统可以提供的附加增益。 二阶系统的总相移近似为 180 度,这导致频率为无穷大。因此,增益裕度也为无穷大。 因此,正确答案是选项 (b)。 32) 求给定开环传递函数的相位交叉频率 G(s) = 1 / s(s + 1) (2s + 1)
答案: (c) 0. 707 弧度/秒 解释: 给定的开环传递函数是:G(s) = 1 / s(s + 1) (2s + 1)  相位交叉频率处的系统虚部为零。因此,我们将虚部设为零,如下所示  这意味着系统的相位交叉频率为 0.707 弧度/秒。 因此,正确答案是选项 (c)。 33) 求给定开环反馈控制系统 G(s)H(s) = 1 / [(s + 1) ^3] 的增益裕度
答案: (c) 8 解释: 给定的开环反馈控制系统是:G(s)H(s) = 1 / [(s + 1) ^3] 交叉频率处的相位角可以通过以下方式计算 -3 tan-1 ω=-180° 我们得到 ω=√3 的值 现在,增益裕度是传递函数的模,如下所示 = 1 / |G(s)H(s)| = |(j√3+13| = 8 因此,正确答案是选项 (c)。 34) 给定系统 G(s) = 1 / [(s + 1) ^3] 的相位裕度是
答案: (a) Π 解释: 相位裕度可以计算为:180 + ∅ 其中, ∅ 是增益交叉频率处的 G(jω) 的相位。 我们首先求给定系统的模,如下所示  因此,正确答案是选项 (a)。 35) 波特图中的转角频率是
答案: (d) 两条渐近线汇合的频率。 解释: 波特图中两条渐近线汇合的频率称为转角频率。 因此,正确答案是选项 (d)。 36) 以下哪些陈述是正确的? 1. 波特图在频域中。 2. 根轨迹在时域中。 3. 奈奎斯特判据在频域中。 4. 劳斯-赫尔维茨判据在时域中。
答案: (b) 1 and 3 解释: 波特图定义为系统正弦传递函数的频率响应图。波特图的两个图是幅度和相角的图。因此,它在频域中。 奈奎斯特图被认为是极坐标图的延伸。频率从无穷大到无穷小的变化会产生图,称为奈奎斯特图。因此,奈奎斯特判据在频域中。 因此,正确答案是选项 (b)。 37) 求给定奈奎斯特图的类型和阶数 
答案: (d) 0, 2 解释: 给定图的类型是 1/ (ST1 + 1)(ST2 + 1) 上述传递函数阶数为 2,类型为 0。 因此,正确答案是选项 (d)。 38) 计算相位裕度为 45 度的系统的阻尼比。
答案: (b) 0.42 解释: 使用相位裕度计算阻尼比的公式是 阻尼比 = tan∅√cos ∅⁄2 = ((tan45√cos45))⁄2 = 0. 42 因此,正确答案是选项 (b)。 39) 单位反馈系统传递函数为 1/ (s + 5)^3 的 GM 是
答案: (c) 60 dB 解释: 相位裕度可以计算为  增益裕度 (GM) = 20 log (1 / |G(s)H(s)|) 在 s = jω 时 我们得到:(GM) = 60dB 因此,正确答案是选项 (c)。 40) 最强大的控制器是
答案: (c) PID 控制器 解释: PID 是比例、积分和微分控制模式的组合。这种组合使其成为最强大的控制器。 因此,正确答案是选项 (c)。 41) 如果误差从 0 开始以 1.2%/s 的速率变化,则在 t = 2s 时 PD 控制器的控制器输出是多少?给定参数为 Po = 50%,Kp = 4,KD = 0.4。
答案: (a) 61. 52% 解释: 误差率 1.2%/秒可以计算为 e = 1.2% x 2 = 1.2/100 x 2 = 2.4% 现在,让我们计算 Pout (控制器输出) = 4 (2.4%+ KD x 1.2%) + Po = 4 (2.4 / 100 + 0.4 x 1.2 /100) + 50/100 = 4 x 2.88/100 + 50/100 = 11.52/100 + 50/100 = 61.52/100 = 61.52% 因此,正确答案是选项 (a)。 42) 用于处理快速过程负载变化的控制器是
答案: (a) PD 控制器 解释: 比例微分控制器用于处理快速过程负载变化。 因此,正确答案是选项 (a)。 43) 考虑以下陈述 1. 超前补偿器增加了系统的带宽。 2.滯後补偿器抑制了稳态性能。 3. 超前补偿器改善了动态响应并提供了更快的响应。 4. 滞后补偿器充当低通滤波器。 在以上陈述中,以下哪些是正确的?
答案: (c) 解释: 滞后补偿器不会抑制稳态性能。相反,它改善了稳态性能。 因此,正确答案是选项 (c)。 44) 补偿网络的传递函数形式为 (1 +aTs) / (1 + Ts)。如果给定网络是滞后网络,求 'a' 的值。
答案: (a) 介于 0 和 1 之间 解释: 给定的传递函数是 (1 +aTs) / (1 + Ts) 我们将首先计算给定传递函数的极点和零点。 此处, 零点 = -1/aT 极点 = -1/T 给定系统中的极点更接近 jω 轴(原点)。零点将远离轴,使得 a 的值 < 1。这意味着该值介于 0 和 1 之间。 因此,正确答案是选项 (a)。 45) 考虑以下陈述 相位超前 1) 增加系统的带宽 2) 改善阻尼 3) 减少稳态误差 4) 增加高频增益 以下哪些陈述是正确的?
答案: (d) 解释: 相位超前负责改善阻尼和减小系统的稳态误差。 因此,正确答案是选项 (d)。 46) 求给定传递函数 G(s) = (1 + 6s)/ (1 + 2s) 的超前补偿器提供的相移
答案: (b) 30 度 解释: 超前补偿器提供的相移可以使用公式计算  超前补偿器的标准传递函数表示为 (s +1/aT) / (s + 1/bT) 将给定传递函数的值与标准传递函数进行比较,我们得到 a = 1/6 b = 1/2 将 a 和 b 的值代入相移公式 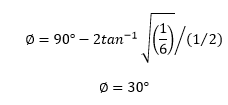 因此,正确答案是选项 (b)。 47) 以下一组微分方程描述了一个线性二阶单输入连续时间系统。 X1'(t) = -2X1(t) + 4X2(t) 这里,X1(t) 和 X2(t) 是状态变量,u(t) 是控制变量。检查系统是否为
答案: (b) 可控但不稳定 说明 我们知道,  此处,  矩阵 A 和 B 的乘积是,  因此,系统的秩为 2。 系统行列式非零。因此,系统是可控的。 现在,我们将检查稳定性。 SI - A = 0  上述矩阵可以用方程形式写成 s^2 + 3s -6 = 0 现在,我们将使用劳斯阵列表查找根,如下所示  第一个列中有两个符号变化。因此,系统不稳定。 因此,正确答案是选项 (b)。 48) 给定矩阵的特征值之和是
答案: (d) 主对角线元素之和 解释: 给定矩阵的特征值之和通常称为矩阵的迹。矩阵的迹是矩阵对角线元素之和。 因此,正确答案是选项 (d)。 49) 考虑由给定微分方程描述的 LTI 系统 d^2 a(t)/dt^2 + 3da(t)/dt + 2a(t) = r(t) 其中 a(t) 是输出。给定特征方程的特征值是
答案: (d) 解释: 令 x1(t) = a(t) 和 x2(t) = ẋ1 因此,给定特征方程可以写成 ẋ2 +3x2 + 2x1 = r(t) 矩阵表示将是  其中,A 是矩阵  我们知道计算特征值的特征方程是 |SI - A| = 0 由此形成的方程是 s (s + 3) + 2 = 0 s^2 + 3s + 2 = 0 s^2 + 2s + s + 2 = 0 (用于查找特征值的分解) (s + 2)(s + 1) = 0 S = -2, -1 因此,所需的特征值是 -2 和 -1。 因此,正确答案是选项 (d)。 50) 图中的信号流图具有 
答案: (c) 前向路径 = 3,环路 = 3,不相交环路 = 0 解释: 前向路径是从输入节点到输出节点在给定信号流图中的路径。这里有三个前向路径。 给定信号流图中的环路数量为三个,如下图所示  不相交环路被视为不相交,当它们之间没有公共节点时。在给定的信号流图中没有不相交的环路。这是因为所有环路都相互接触。 因此,正确答案是选项 (c)。 51) 按顺序排列以下陈述集。 获得自由体图, 1. 通过标记作用在节点上的所有力
答案: (b) 2, 1, 5, 3, 4 解释: 查找自由体图传递函数的正确顺序如下 通过分别绘制每个质量并标记作用在节点上的所有力来创建自由体图。为每个自由体图写一个微分方程,并对微分方程进行拉普拉斯变换,将微分方程转换为代数方程。在 s 域中重新排列方程,通过消除不需要的变量来找到输出和输入之比。这样,我们可以轻松计算自由体图的传递函数。 因此,正确答案是选项 (b)。 下一主题控制系统面试题 |
我们请求您订阅我们的新闻通讯以获取最新更新。