Java 中的七段显示问题

2025年3月17日 | 阅读 7 分钟

七段显示器是一种输出显示设备。它提供了一种以图像、文本或十进制数字形式显示信息的方式。它是复杂点阵显示器的替代品。七段显示器广泛应用于计算器、手表、游戏机、电子仪表等数字或电子设备中。在本节中，我们将讨论如何在 Java 中以七段显示器表示数字。

什么是七段显示器？

它是一种显示设备，通过使用七个 LED 段（水平和垂直条）来形成数字，看起来像数字 8。这些七个段可以形成从 0 到 9 的任何数字。例如，请看下图。

七段显示器的工作原理

下表描述了数字和对应的段代码，其中 0 表示无电源，1 表示有电源。

数字	段数显示数字	七段代码
数字	段数显示数字	a	b	C	d	e	f	g
0	6	1	1	1	1	1	1	0
1	2	0	1	1	0	0	0	0
2	5	1	1	0	1	1	0	1
3	5	1	1	1	1	0	0	1
4	4	0	1	1	0	0	1	1
5	5	1	0	1	1	0	1	1
6	6	1	0	1	1	1	1	1
7	3	1	1	1	0	0	0	0
8	7	1	1	1	1	1	1	1
9	6	1	1	1	0	0	1	1

我们观察到表示一个数字所需的最小段数为 2。

在继续解决方案之前，我们首先将看到显示七段数字的 Java 程序。

在 Java 中以七段形式表示数字的程序

有两种方法可以以七段形式打印数字

使用 switch-case
使用十六进制编码

使用 switch-case

这是以七段显示器形式打印数字的简单方法。在以下 Java 程序中，我们从用户读取一个数字并切换到相应的 case，该 case 将数字打印为七段显示器。

DisplaySevenSegment.java

import java.util.*;
public class DisplaySevenSegment
{
public static void main(String args[]) throws Exception 
{
Scanner sc = new Scanner(System.in);
System.out.print("Enter a digit you want to display: ");
//reads a digit from the user
int n = sc.nextInt();
//switch to the corresponding digit case
switch(n)
{
      case 0:
        System.out.println(" _ \n| | \n|_|");
        break;
      case 1:
        System.out.println("   \n  |\n  |");
        break;
      case 2:
        System.out.println(" _ \n _|\n|_ ");
        break;
      case 3:
        System.out.println(" _ \n _|\n _|");
        break;
      case 4:
        System.out.println("   \n|_|\n  |");
        break;
      case 5:
        System.out.println(" _ \n|_ \n _|");
        break;
      case 6:
        System.out.println(" _ \n|_ \n|_|");
        break;
      case 7:
        System.out.println(" _ \n  |\n  |");
        break;
      case 8:
        System.out.println(" _ \n|_|\n|_|");
        break;
      case 9:
        System.out.println(" _ \n|_|\n _|");
        break;
    }
  }
}

输出 1

让我们看看另一种在七段显示器中打印数字的方法。

使用十六进制编码

在以下 Java 程序中，我们使用十六进制编码来以七段形式表示数字。下表描述了相同的内容。在表中，on 表示 1，off 表示 0。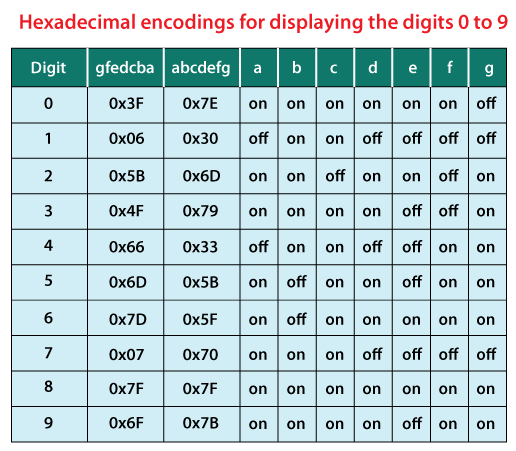

让我们在 Java 程序中实现上述逻辑。

DisplayDigitSevenSegment.java

import java.util.HashMap;
import java.util.Map;
public class DisplayDigitSevenSegment 
{
private static final Map<Integer, Integer> encodings = new HashMap<Integer, Integer>();
//static block that stores key and corresponding values to the Map
//key-digit, value-hexadecimal encoding for displaying the digits 0 to 9 (in abcdefg sequence) 
static 
    {
        encodings.put(0, 0x7E);
        encodings.put(1, 0x30);
        encodings.put(2, 0x6D);
        encodings.put(3, 0x79);
        encodings.put(4, 0x33);
        encodings.put(5, 0x5B);
        encodings.put(6, 0x5F);
        encodings.put(7, 0x70);
        encodings.put(8, 0x7F);
        encodings.put(9, 0x7B);
    }
//driver code    
public static void main(String args[]) throws Exception 
    {
        //loop runs from 0 to 9 and print digits one by one by invoking the print method
        for (int i = 0; i < 10; i++) 
        {
            //calling the print method that prints the digit on the console
            printDigit(i);
        }
    }
//print method that computes how many segments are required to print a digit    
public static void printDigit(int digit) 
    {
        int code = encode(digit);
        char[] bits = String.format("%7s", Integer.toBinaryString(code)).replace(' ', '0').toCharArray();
        lightSegment(bits[0] == '1', " _ \n", "   \n");
        lightSegment(bits[5] == '1', "|", " ");
        lightSegment(bits[6] == '1', "_", " ");
        lightSegment(bits[1] == '1', "|\n", " \n");
        lightSegment(bits[4] == '1', "|", " ");
        lightSegment(bits[3] == '1', "_", " ");
        lightSegment(bits[2] == '1', "|\n", " \n");
    }
//the function decides which segment to be on or off
private static void lightSegment(boolean on, String onValue, String offValue) 
    {
        System.out.print(on ? onValue : offValue);
        try 
        {
            Thread.sleep(100);
        }
        catch (InterruptedException e) 
        {
            e.printStackTrace();
        }
    }
private static int encode(int digit) 
    {
        return encodings.containsKey(digit) ? encodings.get(digit) : 0x00;
    }
}

输出

问题陈述

该问题分为以下两个子问题。

在第一个子问题中，我们将计算显示数字所需的最小段数。
在第二个子问题中，我们将找到使用最小段数来显示数字的元素。

让我们逐一讨论子问题。

子问题 1

我们给定一个 N 位数字，我们必须找到显示每个数字所需的最小段数。将所有段加起来并返回显示 N 位数字的总段数。

示例

假设，N=6（数字位数）且 s="234567"。

表示数字 2 所需的最小段数为 5。

表示数字 3 所需的最小段数为 5。

表示数字 4 所需的最小段数为 4。

表示数字 5 所需的最小段数为 5。

表示数字 6 所需的最小段数为 6。

表示数字 7 所需的最小段数为 3。

因此，我们所需的总段数为 28 (5 + 5 + 4 + 5 + 6 + 3)。

让我们在 Java 程序中实现上述方法。

SegmentSum.java

public class SegmentSum
{
//stored number of segments from 0 to 0
static int []seg = { 6, 2, 5, 5, 4, 5, 6, 3, 7, 6};
//return the number of segments used by x
static int computeSegment(int x)
{
if (x == 0)
return seg[0];
int count = 0;
//finding sum of the segment used by each digit of a number
while (x > 0)
{
count = count+seg[x % 10];
x = x/10;
}
//reyurns number of segments for each number
return count;
}
//driver program
static public void main (String args[])
{
int []arr = {489, 206, 745, 123, 756, 3333};
int n = arr.length;
System.out.println("Number of segments for each number are:");
//loop iterates over the array
for (int i=0; i<arr.length; i++)
{
System.out.println(arr[i]+" = "+computeSegment(arr[i])); 
}
}
}

输出

子问题 2

在这个问题中，我们给定一个自然数数组。任务是找出哪个自然数使用最少段数来显示该数字。可能存在多个自然数具有最少段数的情况，在这种情况下，输出将是索引最小的数字。

例如，考虑以下数组。

arr[] = {22, 46, 88, 12, 67, 90, 23, 55, 61}

22 -> 5+5 = 10

46 -> 4+6 = 10

88 -> 7+7 = 14

12 -> 2+5 = 7

67 -> 6+3 = 9

90 -> 6+6 = 12

23 -> 5+5 = 10

55 -> 5+5 = 10

61 -> 5+5 = 8

我们观察到数字 12 使用最少的段数来显示该数字。因此，输出将是 12。

在七段显示器中查找使用最少段数的元素的 Java 程序

在以下 Java 程序中，我们存储了每个数字的段数。之后，我们定义了两个函数，一个计算数字的段数，第二个函数计算整个数字的最小段数。之后，我们将每个数字的段数相互比较，并返回使用最少段数的数字。

让我们看看相应的 Java 程序。

SevenSegment.java

import java.io.*;
public class SevenSegment 
{
//precomputed values of segment used by digit 0 to 9
static int []seg = { 6, 2, 5, 5, 4, 5, 6, 3, 7, 6};
//return the number of segments used by x.
static int computeSegment(int x)
{
if (x == 0)
return seg[0];
int count = 0;
//finding sum of the segment used by each digit of a number
while (x > 0)
{
count = count + seg[x % 10];
x = x / 10;
}
return count;
}
static int elementMinSegment(int []arr, int n)
{
//initializing the minimum segment and minimum number index
int minseg = computeSegment(arr[0]);
int minindex = 0;
//finding and comparing segment used by each number arr[i]
for (int i = 1; i < n; i++)
{
int temp = computeSegment(arr[i]);
//if arr[i] used less segment then update the minimum segment and minimum number
if (temp < minseg)
{
minseg = temp;
minindex = i;
}
}
return arr[minindex];
}
//driver code
public static void main (String args[])
{
int []arr = {22, 46, 88, 12, 67, 90, 23, 55, 61};
//determines the length of the array
int n = arr.length;
//function calling
System.out.println(elementMinSegment(arr, n));
}
}

输出

复杂度

上述方法的时间复杂度为 O(n * log₁₀n)，空间复杂度为 O(1)。

下一个主题Java 中的拆分数组最大和

Java 中的七段显示问题

什么是七段显示器？

七段显示器的工作原理

在 Java 中以七段形式表示数字的程序

使用 switch-case

使用十六进制编码

问题陈述

子问题 1

子问题 2

在七段显示器中查找使用最少段数的元素的 Java 程序

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

Java 程序

Java 中的七段显示问题

什么是七段显示器？

七段显示器的工作原理

在 Java 中以七段形式表示数字的程序

使用 switch-case

使用十六进制编码

问题陈述

子问题 1

子问题 2

在七段显示器中查找使用最少段数的元素的 Java 程序

相关帖子

将字符串分成 'N' 等份的 Java 程序

Java 打印螺旋图案的程序

如何在 Java 中将 long 转换为 int

如何在 Java 中将 double 转换为字符串

Java 中将零移到末尾

Java 中的二分搜索

Java 从双向链表开头删除新节点的程序

查找具有 N 个键的可能二叉搜索树总数的 Java 程序

如何在 Java 中将字符串转换为 double

Java 中从双精度数组中查找原始数组

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器