用于识别范式的问题

要解决识别范式的题目，我们必须理解BCNF、3NF和2NF的定义

2NF定义：任何非主属性都不能部分依赖于候选键。也就是说，不应该存在X → Y的部分依赖。

3NF定义：首先，它必须是2NF，并且如果存在两个属性集X和Y之间的非平凡依赖关系X → Y（即Y不是X的子集），则

1. X是超键
2. 或者Y是主属性。

BCNF定义：首先，它必须是3NF，并且如果存在两个属性集X和Y之间的非平凡依赖关系X → Y（即Y不是X的子集），则

1. X是超键

注意：如果一个表是BCNF，那么它也是3NF、2NF和1NF；同样，如果表是3NF，那么它也是2NF和1NF。因此，我们可以说，如果一个表处于较高的范式，那么它默认就处于较低的范式。

问题 1：给定一个关系 R( P, Q, R, S, T, U, V, W, X) 和函数依赖集 FD = { PQ → R, QS → TU, PS → VW, and P → X }，请确定给定的R属于哪个范式？

解：让我们使用FD在R上构建一个箭头图来计算候选键。

从上面R上的箭头图可以看出，属性PQS不能被给定的任何FD确定，因此PQS将是候选键的组成部分，即无论候选键是什么，有多少个候选键，但所有候选键都必须包含PQS这个必填属性。

让我们计算 PQS 的闭包

PQS + = P Q R S T U X V W （根据我们之前学过的闭包方法）

由于PQS的闭包包含了R的所有属性，因此PQS是候选键

根据候选键的定义（候选键是超键，其任何真子集都不是超键）

由于所有键都将PQS作为组成部分，并且我们已经证明PQS是候选键，因此，PQS的任何超集都将是超键，但不是候选键。

因此，只有一个候选键PQS

由于R有9个属性：- P, Q, R, S, T, U, V, W, X，并且候选键是PQS，因此，主属性（候选键的一部分）是P Q和S，而非主属性是R T U V W X

给定的FD是 { PQ → R, QS → TU, PS → VW, and P → X }，超键/候选键是PQS

注意：要解决此类问题，我们应用逆向工程，即首先检查BCNF，如果不满足则检查3NF，如果不满足则检查2NF，以此类推。

1. FD: PQ → R 不满足BCNF的定义，因为PQ不是超键，因此该表不是BCNF（因为一个依赖不满足，所有依赖都不满足）。现在我们检查相同的FD对于3NF。
2. FD: PQ → R 甚至不满足3NF的定义，因为PQ不是超键，也不是R是主属性，因此该表也不是3NF（因为一个依赖不满足，所有依赖都不满足）。现在我们检查相同的FD对于2NF
3. FD: PQ → R 甚至不满足2NF的定义，因为PQ不是超键，也不是主属性，并且R是非主属性依赖于键的一部分（部分依赖），因此该表也不是2NF（因为一个依赖不满足，所有依赖都不满足）。

因此，根据以上三个陈述，我们可以说表 R ( P, Q, R, S, T, U, V, W, X) 仅是1NF。

问题 2：给定一个关系 R( P, Q, R, S, T, U, V, W ) 和函数依赖集 FD = { PQ → R, P → ST, Q → U, and U → VW }，确定给定的R属于哪个范式？

解：让我们使用FD在R上构建一个箭头图来计算候选键。

从上面R上的箭头图可以看出，属性PQ不能被给定的任何FD确定，因此PQ将是候选键的组成部分，即无论候选键是什么，有多少个候选键，但所有候选键都必须包含PQ这个必填属性。

让我们计算 PQ 的闭包

PQ + = P Q R S T U V W （根据我们之前学过的闭包方法）

由于PQ的闭包包含了R的所有属性，因此PQ是候选键

根据候选键的定义（候选键是超键，其任何真子集都不是超键）

由于所有键都将PQ作为组成部分，并且我们已经证明PQ是候选键，因此，PQ的任何超集都将是超键，但不是候选键。

因此，只有一个候选键PQ

由于R有8个属性：- P, Q, R, S, T, U, V, W，并且候选键是PQ。因此，主属性（候选键的一部分）是P和Q，而非主属性是R S T U V W

给定的FD是 { PQ → R, P → ST, Q → U, and U → VW }，超键/候选键是PQ

注意：要解决此类问题，我们应用逆向工程，即首先检查BCNF，如果不满足则检查3NF，如果不满足则检查2NF，以此类推。

1. FD: PQ → R 满足BCNF的定义，因为PQ是超键，因此无需检查它是否满足更高的范式，因为它满足最高的范式。现在我们以逆向工程的方式检查另一个依赖关系。
2. FD: P → ST 不满足BCNF的定义，因为P不是超键，因此该表不是BCNF（因为一个依赖不满足，所有依赖都不满足）。现在我们检查相同的FD对于3NF。
3. FD: P → ST 甚至不满足3NF的定义，因为P不是超键，也不是S T是主属性，因此该表也不是3NF（因为一个依赖不满足，所有依赖都不满足）。现在我们检查相同的FD对于2NF。
4. FD: P → ST 甚至不满足2NF的定义，因为P不是超键，也不是主属性，并且S T是非主属性依赖于键的一部分（部分依赖），因此该表也不是2NF（因为一个依赖不满足，所有依赖都不满足）。

因此，根据以上三个陈述b、c和d，我们可以说表 R ( P, Q, R, S, T, U, V, W, ) 仅是1NF。

问题 3：给定一个关系 R( P, Q, R, S, T, U ) 和函数依赖集 FD = { PQ → R, SR→ PT, T → U }，确定给定的R属于哪个范式？

解：让我们使用FD在R上构建一个箭头图来计算候选键。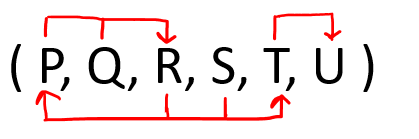

从上面R上的箭头图可以看出，属性QS不能被给定的任何FD确定，因此QS将是候选键的组成部分，即无论候选键是什么，有多少个候选键，但所有候选键都必须包含QS这个必填属性。

让我们计算 QS 的闭包

QS + = QS （根据我们之前学过的闭包方法）

由于QS的闭包不包含R的所有属性，因此QS不是候选键。

在将QS与其他属性组合后，我们发现PQS和RQS可以确定R的所有属性，因此PQS和RQS是R的候选键。

由于R有6个属性：- P, Q, R, S, T, U，候选键是PQS和RQS，因此，主属性（候选键的一部分）是P Q R和S，而非主属性是T U

给定的FD是 { PQ → R, SR→ PT, T → U }，超键/候选键是PQS和RQS

注意：要解决此类问题，我们应用逆向工程，即首先检查BCNF，如果不满足则检查3NF，如果不满足则检查2NF，以此类推。

1. FD: PQ → R 不满足BCNF的定义，因为PQ不是超键，因此该表不是BCNF（因为一个依赖不满足，所有依赖都不满足）。现在我们检查相同的FD对于3NF
2. FD: PQ → R 满足3NF的定义，即使PQ不是超键，但R是属性，因此该表是3NF。现在我们使用逆向工程过程检查其他FD。
3. FD: SR → PT 不满足3NF的定义，因为SR不是超键，也不是P T是主属性（因为P是主属性，但组合必须是主属性），因此该表不是3NF（因为一个依赖不满足，所有依赖都不满足）。现在我们检查相同的FD对于2NF
4. FD: SR → PT 不满足2NF的定义，因为SR不是超键，也不是主属性，并且P T是非主属性依赖于键的一部分（部分依赖），因此该表也不是2NF（因为一个依赖不满足，所有依赖都不满足）。

因此，根据以上两个陈述c和d，我们可以说表 R ( P, Q, R, S, T, U) 仅是1NF。

问题 4：给定一个关系 R( P, Q, R, S, T) 和函数依赖集 FD = { QR → PST, S → Q }，确定给定的R属于哪个范式？

解：让我们使用FD在R上构建一个箭头图来计算候选键。

从上面R上的箭头图可以看出，属性R不能被给定的任何FD确定，因此R将是候选键的组成部分，即无论候选键是什么，有多少个候选键，但所有候选键都必须包含R这个必填属性。

让我们计算 R 的闭包

R + = R （根据我们之前学过的闭包方法）

由于R的闭包不包含R的所有属性，因此R不是候选键。

在将R与其他属性组合后，我们发现RS和RQ可以确定R的所有属性，因此RS和RQ是R的候选键。

由于R有5个属性：- P, Q, R, S, T，候选键是RS和RQ，因此主属性（候选键的一部分）是S Q R，而非主属性是TP

给定的FD是 { QR → PST, S → Q }，超键/候选键是RS和RQ

注意：要解决此类问题，我们应用逆向工程，即首先检查BCNF，如果不满足则检查3NF，如果不满足则检查2NF，以此类推。

1. FD: QR → PST 满足BCNF的定义，因为QR是超键，我们检查其他FD是否满足BCNF
2. FD: S → Q 不满足BCNF的定义，因为S不是超键，因此该表不是BCNF（因为一个依赖不满足，所有依赖都不满足）。现在我们检查相同的FD对于3NF
3. FD: S → Q 满足3NF的定义，即使S不是超键，但Q是主属性，因此该表是3NF。

由于只有两个FD，其中一个（QR → PST）满足BCNF，而另一个（S → Q）满足3NF，因此最高范式是3NF。R(P, Q, R, S, T) 是3NF。

问题 5：给定一个关系 R( A, B, C) 和函数依赖集 FD = { A → B, B → C, and C → A}，确定给定的R属于哪个范式？

解：让我们使用FD在R上构建一个箭头图来计算候选键。

从上面R上的箭头图可以看出，所有属性都可以通过给定的FD的所有属性来确定，因此我们将检查所有属性（即A、B和C）是否为候选键

让我们计算 A 的闭包

A + = ABC （根据我们之前学过的闭包方法）

由于A的闭包包含了R的所有属性，因此A是候选键。

让我们计算 B 的闭包

B + = BAC （根据我们之前学过的闭包方法）

由于B的闭包包含了R的所有属性，因此B是候选键。

让我们计算 C 的闭包

C + = CAB （根据我们之前学过的闭包方法）

由于C的闭包包含了R的所有属性，因此C是候选键。

因此，三个候选键是：A B 和 C

由于R有3个属性：- A B 和 C，候选键是A B 和 C，因此，主属性（候选键的一部分）是A B C，而没有非主属性

给定的FD是 { A → B, B → C, and C → A }，超键/候选键是A B 和 C

注意：要解决此类问题，我们应用逆向工程，即首先检查BCNF，如果不满足则检查3NF，如果不满足则检查2NF，以此类推。

1. FD: A → B 满足BCNF的定义，因为A是超键，我们检查其他FD是否满足BCNF
2. FD: B → C 满足BCNF的定义，因为B是超键，我们检查其他FD是否满足BCNF
3. FD: C à A 满足BCNF的定义，因为C是超键

由于只有三个FD，并且所有FD：{ A → B, B → C and C → A } 都满足BCNF，因此最高范式是BCNF。

因此R(A, B, C ) 是BCNF。

结论：从以上三个例子，我们可以得出结论，识别关系模式的范式遵循以下步骤：

步骤 1：通过箭头图和属性在R上的闭包来计算给定R的候选键，从而从计算出的候选键中分离出主属性和非主属性。

步骤 2：以逆向工程的方式验证每个FD，即首先检查BCNF，如果不满足则检查3NF，如果不满足则检查2NF，以此类推。

步骤 3：如果一个表是BCNF，那么它也是3NF、2NF和1NF；同样，如果表是3NF，那么它也是2NF和1NF。因此，我们可以说，如果一个表处于较高的范式，那么它默认就处于较低的范式。

步骤 4：首先使用BCNF定义验证第一个FD（首先它必须是3NF，并且如果存在两个属性集X和Y之间的非平凡依赖关系X → Y（即Y不是X的子集），则X是超键。

步骤 5：如果任何FD步骤 5失败（表示表不是BCNF），则使用3NF定义验证该FD和其余FD（首先它必须是2NF，并且如果存在两个属性集X和Y之间的非平凡依赖关系X → Y（即Y不是X的子集），则X是超键或Y是主属性

步骤 6：如果任何FD步骤 6 失败（表示表不是BCNF），则使用2NF定义验证该FD和其余FD（非主属性不能部分依赖于表的键）。

步骤 7：如果任何FD步骤 7 失败（表示表不是2NF），则无需检查1NF，因为它默认是1NF。

步骤 8：如果所有FD都满足BCNF的定义，那么我们可以说给定的R是BCNF；如果任何FD不满足BCNF，而该FD和其余FD满足3NF，那么我们说R是3NF；类似地，如果任何FD不满足3NF，而该FD和其余FD满足2NF，那么我们说R是2NF，否则该表是1NF。