外部排序合并算法

到目前为止，我们已经看到排序是任何数据库系统中的一个重要术语。它意味着以升序或降序排列数据。我们不仅使用排序来生成有序的输出，还用于满足各种数据库算法的条件。在查询处理中，排序方法用于高效地执行各种关系操作，如连接等。但需要向系统提供已排序的输入值。为了对任何关系进行排序，我们必须在排序键上建立索引，并使用该索引以排序的顺序读取关系。但是，使用索引，我们是逻辑上排序关系，而不是物理上排序。因此，排序用于包含以下情况的场景：

情况 1：关系的大小小于或等于主内存。

情况 2：关系的大小大于内存大小。

在情况 1 中，大小较小或中等的关系不会超过主内存的大小。因此，我们可以将其放入内存。所以，我们可以使用标准排序方法，如快速排序、合并排序等来完成。

对于情况 2，标准算法无法正常工作。因此，对于大小超过内存大小的关系，我们使用外部排序-合并算法。

对不适合内存的关系进行排序，因为它们的大小大于内存大小。这种排序称为外部排序。因此，外部排序-合并是最适合外部排序的方法。

外部排序合并算法

在这里，我们将详细讨论外部排序-合并算法的各个阶段

在算法中，M 表示用于排序的主内存缓冲区中可用的磁盘块数量。

阶段 1：最初，我们创建一定数量的已排序的运行。对每个运行进行排序。这些运行包含关系中只有少量记录。

在阶段 1 中，我们可以看到我们正在对磁盘块执行排序操作。完成阶段 1 的步骤后，继续进行阶段 2。

阶段 2：在阶段 2 中，我们合并运行。假设运行的总数 N 小于 M。因此，我们可以为每个运行分配一个块，并且仍然有剩余空间来容纳一个输出块。我们按如下方式执行操作：

完成阶段 2 后，我们将获得一个已排序的关系作为输出。然后对输出文件进行缓冲以最小化磁盘写操作。由于此算法合并 N 个运行，因此称为N 路合并。

然而，如果关系的大小大于内存大小，那么在阶段 1 中将生成 M 个或更多运行。此外，在处理阶段 2 时，不可能为每个运行分配一个块。在这种情况下，合并操作过程需要多次传递。由于 M-1 个输入缓冲区块具有足够的内存，因此每次合并都可以轻松地容纳 M-1 个运行作为其输入。因此，初始阶段按以下方式工作：

• 它合并前 M-1 个运行，以获得下一个运行的单个运行。
• 类似地，它合并接下来的 M-1 个运行。此步骤将一直继续，直到处理完所有初始运行。此时，运行的数量减少了 M-1。但是，如果这个减小后的值大于或等于 M，我们需要创建另一个传递。对于这个新传递，输入将是第一个传递创建的运行。
• 每个传递的工作是每次将运行数量减少 M-1。此任务会根据需要重复执行，直到运行的数量小于或等于 M。
• 因此，最终传递会产生排序的输出。

外部排序-合并方法的成本估算

外部排序-合并的成本分析是使用算法中讨论的上述阶段进行的。

• 假设 b_r 表示包含关系 r 记录的块数。
• 在第一阶段，它读取关系的每个块并将其写回。总共需要 2b_r 次块传输。
• 最初，运行的数量为 [b_r/M]。由于在每次合并传递中，运行的数量减少了 M-1，因此总共需要 [log _M-1(b_r/M)] 次合并传递。

每次传递仅读取和写入关系的每个块一次。但有两个例外：

• 最终传递可以在不将其结果写入磁盘的情况下提供排序的输出。
• 可能存在某些运行在传递期间未被读取或写入的情况。

忽略这些小的例外情况，外部排序的总块传输次数为：

b _r (2 Γ log _M-1 (b _r /M) ˥ + 1)

我们需要添加磁盘寻道成本，因为每个运行都需要读取和写入数据的寻道。如果在阶段 2（即合并阶段）中，每个运行分配了 b_b 个缓冲区块，或者每个运行一次读取 b_b 个数据，那么每次合并需要 [b_r /b_b] 次寻道来读取数据。输出是顺序写入的，因此如果它与输入运行在同一磁盘上，那么磁头在连续块的写入之间需要移动。因此，每次合并传递的总寻道次数增加 2[b_r /b_b]，总寻道次数为：

2 Γ b _r /M ˥ + Γb _r /b _b ˥(2Γlog_M-1(b _r /M)˥ - 1)

因此，我们需要计算磁盘寻道的总数来分析外部合并排序算法的成本。

外部合并排序算法示例

让我们通过一个例子来理解外部合并排序算法的工作原理，并分析外部排序的成本。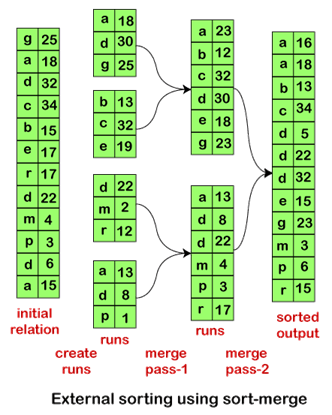

假设我们正在对关系 R 执行外部排序-合并。在此，假设每个块只能容纳一个元组，并且内存最多可以容纳三个块。因此，在处理阶段 2（即合并阶段）时，它将使用两个块作为输入，一个块作为输出。