根轨迹的基本概念

在前面的章节中，我们研究了系统的稳定性。它取决于特征方程的根的位置。我们也可以说系统的稳定性取决于闭环极点的位置。这种关于当参数变化时，极点在 s 平面中运动的知识很重要。参数的微小变化可以极大地帮助系统设计。系统的瞬态响应的性质与 s 平面中极点的位置密切相关。

我们还研究了描述代数方程稳定性的劳斯-赫尔维茨判据。如果劳斯表中第一列中的任何一项发生符号变化，系统则倾向于变得不稳定。

根轨迹法是由 W.R Evans 在 1948 年提出的。根轨迹是一种图形方法，当特定参数从 0 变化到无穷大时，可以在 s 平面中找到极点的位置。假设要变化的参数通常是系统的增益。

考虑下面的闭环系统。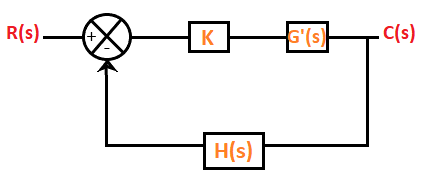

闭环系统的方程由下式给出

1 + G(s)H(s) = 0

其中，

G(s) 是传递函数的增益

H(s) 是反馈增益

在根轨迹的情况下，增益 K 也被认为是闭环系统的一部分。K 称为系统增益或正向路径中的增益。包含正向增益后的特征方程可以表示为

1 + KG'(s)H(s) = 0

其中，

G(s) = KG'(s)

当系统包含可变参数 K 时，闭环系统的根现在取决于“K”的值。

“K”可变值可以在两种情况下变化，如下所示

在第一种情况下，对于 K 的每个不同的值（整数或小数），我们将得到一组单独的根位置。如果连接所有这些位置，则得到的曲线定义为根轨迹。我们还可以将根轨迹定义为当系统增益“K”从 -无穷大 变化到 无穷大时获得的闭环极点的轨迹。

当 K 从 零到无穷大变化时，该图称为直接根轨迹。如果系统增益“K”从负无穷大变化到零，则由此获得的图称为反根轨迹。除非特别说明，否则通常假设增益 K 从零到无穷大。

让我们考虑一个例子。

示例：获得单位反馈系统的根轨迹，其中 G(s) = K/s。

如上所述，这是一个单位反馈系统。这意味着 H(s) = 1。

我们知道，

1 + G(s)H(s) = 0

1 + K/s = 0

S + K = 0

上述方程的根位于 s = -K 处。

根据条件，系统增益 K 从零变化到无穷大，除非状态。因此，当 K 从零变化到无穷大时，我们将通过连接所有这些位置来获得根轨迹。

在 K 的不同值下，给定方程的根的值在下表中给出

下面显示了 K 的上述值的根轨迹图

根轨迹的用途

除了确定系统的稳定性外，根轨迹还有助于确定

• 阻尼比
  阻尼比是一个无量纲单位，描述系统衰减如何影响系统的振荡。
• 自然频率
  它由 w_n 表示。极点位置处的系统增益 K 的值有助于计算系统的自然频率和阻尼比。
• P、PI 和 PID 控制器
  借助根轨迹技术可以设计 P（比例）、PI（比例积分）和 PID（比例积分微分）控制器。在这里，要控制的系统的输入与系统增益 K 成正比。
• 滞后和超前补偿器
  补偿器是系统中添加的附加组件，用于补偿性能不足。相前补偿器有助于将根轨迹移向复 s 平面中的左侧，并进一步提高系统的稳定性。类似地，借助根轨迹可以以各种方式设计滞后和超前补偿器。

根轨迹的优点

根轨迹的优点如下

• 我们可以借助根轨迹图分析系统的绝对稳定性。
• 使用幅值和角度条件，我们可以找到根轨迹上任何点的系统增益 K 的极限值。
• 以更高的精度增强系统设计。
• 它有助于分析具有时延的系统的稳定性。
• 根轨迹图帮助我们确定增益裕度、相对稳定性、相角裕度和系统的稳定时间。
• 与其他控制系统技术相比，根轨迹技术易于实现。
• 它有助于分析控制系统的性能。