根轨迹的规则

我们知道 -2.2 位于 -2 和 -3 之间，而点 -3.4 位于 -3 和 -4 之间。

点 -2.2： 在点 -2.2，右侧的极点和零点的总和为 2，即 1 个极点和 1 个零点。 这意味着总和是偶数。 根据规则 3，总和应该是奇数。 因此，点 -2.2 不位于根轨迹上。 我们也可以说，-2 和 -3 之间的任何点都不会位于根轨迹上。

点 -3.4： 在点 -3.4，右侧的极点和零点的总和为 3，即 1 个极点和 2 个零点。 这意味着总和是奇数。 根据规则 3，总和应该是奇数。 因此，点 -3.4 位于根轨迹上。 我们也可以说，-3 和 -4 之间的任何点都将位于根轨迹上。

点之间的根轨迹区域如下所示

在这里，橙色线表示根轨迹所在的区域。

让我们考虑一个例子以便更好地理解。

示例：G(s)H(s) = K(s + 1)(s + 4)/ s(s + 3)(s + 5)。 找出根轨迹存在于实轴的哪些部分。

解决方案： 我们知道分母表示极点，分子表示零点。 因此，根据给定的传递函数，0、-3 和 -5 是极点，-1 和 -4 是零点。 这意味着有 3 个极点和 2 个零点。

这些极点和零点在实轴上将显示为

根据规则 3，

• 0 和 -1 之间 的部分（例如，点 -0.4）仅包含一个极点，右侧没有零点。 这意味着总和是奇数（即 1）。 因此，它存在于根轨迹上。
• -1 和 -3 之间 的部分（例如，点 -2.1）在右侧仅包含一个极点和一个零点。 这意味着极点和零点的总和是偶数（即 2）。 因此，它不存在于根轨迹上。
• -3 和 -4 之间 的部分（例如，点 -3.5）在右侧包含两个极点和一个零点。 这意味着总和是奇数（即 3）。 因此，它存在于根轨迹上。
• -4 和 -3 之间 的部分（例如，点 -4.3）在右侧包含两个极点和两个零点。 这意味着极点和零点的总和是偶数（即 4）。 因此，它不存在于根轨迹上。
• 大于 -5 的部分（例如，点 -8.6）在右侧包含三个极点和两个零点。 这意味着总和是奇数（即 5）。 因此，它存在于根轨迹上。

因此，标有橙色的线描绘了根轨迹存在的部分。 如下所示

规则 4

我们已经讨论过 (P - Z) 提供了给定传递函数接近无穷大的分支的数量。 关于这些接近无穷大的分支的信息在规则 4 下定义，称为 渐近线。 这种渐近线的角度由下式给出

= (2q + 1)180 / P - Z

其中，

q = 0, 1, 2, 3, 4 ... (P - Z - 1)

这些总是关于实轴对称的。

规则 5

规则 4 描述了关于接近无穷大的分支的准则或信息，称为渐近线。 但是，角度不足以绘制根轨迹，而且这些分支在 s 平面中的位置也很重要，由规则 5 定义。

质心 是渐近线在实轴上的公共点处相交的点。 它可以计算为

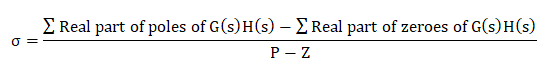
注意：质心的值始终是实数，可以是正数或负数。 它可以是根轨迹的一部分，有时不是。

规则 6

最后一条规则是分离点。 它也是给定方程的多个根发生于根轨迹上的一个点。 它针对系统增益 K 的特定值进行计算。

或

它可以定义为根轨迹上的一个点，在该点处会发生给定 K 值的两个或多个根。

根轨迹分支始终以 180/n 的角度离开分离点。

其中，

N = 接近分离点的分支数。

角度的值可以是正数或负数。

让我们讨论一些关于分离点存在的预测

• 如果两个极点之间的部分位于根轨迹上，则在相邻的极点之间至少存在一个分离点。
  例如：
  G(s)H(s) = K/s(s + 3)

上述传递函数在 0 和 -3 处有两个极点。 根据规则 3，0 和 -3 之间的部分上的点（例如，点 -2.2）在右侧有一个极点和零个零点。 这表明零点和极点的总和为 1，即奇数。 因此，0 和 -3 之间的部分存在于根轨迹上。

因此，它们之间必须至少存在一个分离点。