控制系统：带解释的示例

在这里，我们将讨论与方框图简化、信号流图、梅森增益公式和控制系统基本概念相关的示例。这些示例将基于 MCQ（多项选择题），因为这也有助于应对竞争性考试。

示例 1

求给定方框图的传递函数。

1. 10
2. 7.7
3. 4.5
4. 2.416

答案： (d) 2.416

解： 在给定方框图中，R(s) 是输入，C(s) 是输出。系统的传递函数将是输出与输入之比。它由以下公式给出

C(s)/R(s)

让我们开始解决系统传递函数的步骤。

步骤 1： 我们将首先使用并联的两个方框值相加形成等效方框的规则，合并并联的两个方框。如下图所示

4 + 5 = 9

求解后，方框图现在将显示为

步骤 2： 现在，我们将使用串联的两个方框值相乘形成等效方框的规则，合并串联的方框。如下图所示

9x8 = 72

第二步后的方框图将显示为

我们剩下一个闭环。闭环传递函数由以下公式给出

C(s)/R(s) = 72/1 + 72x 0.4 = 72/29.8 = 2.416

C(s)/R(s) = 2.416

示例 2

线性系统的传递函数由以下公式给出

1. 系统输出 Vo(t) 与输入 Vi(t) 之比。
2. 系统输出 Vo(t) 的导数 dVo(t)/dt 与输入 Vi(t) 的导数 dVi(t)/dt 之比。
3. 系统输出 Vo(s) 与输入 Vi(s) 的拉普拉斯变换之比，且所有初始条件均为零。
4. 系统输出 Vo(s) 与输入 Vi(s) 的傅里叶变换之比。

答案： (c) 系统输出 Vo(s) 与输入 Vi(s) 的拉普拉斯变换之比。

解： 对于给定的方框图或特征方程，线性系统的传递函数始终用拉普拉斯表示。它被计算为系统输入和输出的拉普拉斯变换之比。

例如：

Vo = (1 + t²) Vi

上述方程的传递函数可以通过首先取拉普拉斯变换来计算，它由以下公式给出

Vo (s) = (1/s + 2/s³) Vi(s)

Vo (s)/ Vi(s) = (1/s + 2/s³)

因此，传递函数为 (1/s + 2/s³)。它是在假设所有初始条件均为零的情况下获得的。

示例 3

求给定方框图的传递函数。

1. C(s) = G₁ R₁(s) / (1 + G₁H₁) + G₂R₂(s) /(1 + G₁G₂H₁)
2. C(s) = G₁G₂ R₁(s) / (1 + G₁G₂H₁) + G₂R₂(s) /(1 + G₁G₂H₁)
3. C(s) = G₂ R₁(s) / (1 + G₁G₂H₁) + R₂(s) /(1 + G₁G₂H₁)
4. C(s) = G₁G₂ R₁(s)R₂(s) / (1 + G₁G₂H₁)

答案： (b) C(s) = G₁G₂ R₁(s) / (1 + G₁G₂H₁) + G₂R₂(s) /(1 + G₁G₂H₁)

解： 以上问题是关于多输入系统的。让我们考虑一些可能有助于解决多输入问题的步骤。

1. 考虑一个输入，其他输入为零。
2. 对每个输入执行上述步骤。
3. 重新排列方框图并确定具有单个非零输入的传递函数。
4. 对所有输入重复步骤 3。
5. 将所有传递函数相加得到最终输出。

为了解决上述问题，请遵循以下步骤

步骤 1： 在给定图中，有两个输入 R1 和 R2。让我们首先设置 R1 = 0。

因此排列的方框图将显示为

结果的方框图现在将显示为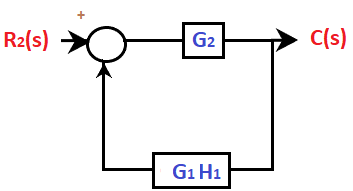

传递函数将是

C₂(s)/R₂(s) = G₂/(1 + G₁G₂H₁)

C₂(s) = G₂R₂(s) /(1 + G₁G₂H₁) ... (1)

步骤 2： 现在假设 R2 = 0

因此排列的方框图将显示为

结果的方框图现在将显示为

传递函数将是

C₁(s)/R₁(s) = G₁G₂/(1 + G₁G₂H₁)

C₁(s) = G₁G₂ R₁(s) / (1 + G₁G₂H₁) ... (2)

现在，将两个方程相加，我们将得到所需的传递函数。它由以下公式给出

C(s) = C₁(s) + C₂(s)

C(s) = G₁G₂ R₁(s) / (1 + G₁G₂H₁) + G₂R₂(s) /(1 + G₁G₂H₁)

C(s) = (G₁G₂ R₁(s) + G₂R₂(s))/( 1 + G₁G₂H₁)

示例 4

系统类型表示

1. 原点的零点数
2. 原点的极点数
3. 无穷远的极点数
4. 有限极点数

答案： (b) 原点的极点数

解： 系统类型通常表示原点的极点数。如果原点有两个极点，则表示该系统是 2 型。1 型表示开环传递函数，在原点有一个极点。同样，我们可以说，如果系统在原点没有极点，则将其归类为 0 型系统。

示例 5

在给定信号流图中，y/x 等于

1. 2.5
2. 8
3. 6
4. 4

答案： (b) 8

解： 信号流图中只有一个回路。回路的增益由以下公式给出

2/( 1 + 2(1)) = 2/3

所有其他分支都串联或级联连接。因此，等效结果将是三个节点上所有值的乘积。

y/x = 4 x 2/3 x 3 = 8

示例 6

信号流图的目的是找到

1. 系统的传递函数
2. 系统的可控性
3. 系统的稳定性
4. 系统的可观测性

答案： (a) 系统的传递函数

解： 控制系统中的信号流图用于查找系统的传递函数，例如梅森增益公式。它专门设计用于查找信号流图的传递函数，包括不相接触的回路和前向路径增益。

示例 7

求给定信号流图的传递函数。

1. 10/9
2. 22/15
3. 44/23
4. 23/24

答案： (c) 44/23

解： 我们知道信号流图的传递函数通常使用梅森增益公式计算，它由以下公式给出

其中，

Pk 是前向路径增益

∆ 是回路增益。

回路增益计算如下

1 - 所有回路增益之和 + 两个不相接触回路增益乘积之和 - 三个不相接触回路增益乘积之和

∆_k 是通过消除所有与前向路径 Pk 相接触的回路来计算的。

让我们讨论给定信号流图的解决方案。

根据给定图表，有两个前向路径。

P1 = 5

P2 = 1x2x3x4 = 24

有四个单独的闭环。

L1 = -5

L2 = -2

L3 = -3

L4 = -4

只有两个不相接触的回路，即 L2 和 L4。这两个回路的乘积是：(-2) x (-4) = 8

因此，给定信号流图的传递函数是

= 5 (1 + 3) + 24/ 1 + (5 + 2 + 3 + 4) + 8

= 44/23

示例 8

求传递函数 F(s) = 4 /s²+2s + 5 的初始值 f(t)，其中 F(s) 是函数 f(t) 的拉普拉斯变换。

1. 4
2. 4/5
3. 0
4. 1

答案： (c) 0

解： 传递函数的初始值由以下公式给出

所以，我们将把 s = 无穷大代入给定的传递函数 F(s) = 4 /s²+2s + 5。

我们得到，

F(s) = 0

示例 9

以下哪项陈述不正确？

1. 传递函数沿信号流图中的分支表示
2. 方框图的简化是一个复杂的过程
3. 传递函数沿方框图中的分支表示
4. 方框图中没有自环

答案： (c) 传递函数沿方框图中的分支表示

解： 让我们详细讨论这四项陈述。

• 传递函数沿信号流图中的分支表示
  信号流图以连接节点的支路形式出现。我们从一端到另一端找到前向路径和支路的增益。因此，第一个陈述是正确的。
• 方框图的简化是一个复杂的过程。
  方框图的简化涉及各种步骤，因为有必要在每个步骤绘制方框图。简化需要仔细遵循。因此，第二个陈述也是正确的。
• 传递函数沿方框图中的分支表示。
  在方框图的情况下，传递函数在方框内部表示，而不是沿分支表示。因此，第三个陈述是不正确的。
• 方框图中没有自环。
  自环存在于信号流图的情况下。因此，最后一个陈述是正确的。

示例：10

给定方框图的传递函数是

1. -1.714
2. 1. 714
3. -2.9
4. 1.59

答案： (a) -1.714

解： 在这里，给定的方框图有三个回路。所以，我们首先解决这三个回路。

步骤 1、2 和 3 如下所示

步骤 1： 它有一个方框和一个并联的单位线。当单位线与方框并联时，它被认为是 1。根据规则，并联方框的等效值相加。所以，

= 2 + 1 = 3

步骤 2： 它包含两个方框，其中一个方框存在于反馈路径中。

所以，我们将使用传递函数公式，其中 G(s) 和 H(s) 分别为 1.5 和 1。

= 1.5/1 + 1.5x2

= 1.5/4

步骤 3： 级联中的前两个方框将相乘。

= 5 x -8 = -40

它有一个值为 0.6 的反馈路径。所以，我们将使用以下传递函数公式

G(s)/1 - G(s)H(s)

其中，G(s) 和 H(s) 分别为 -40 和 0.6。

方框的结果值将是：-40/ 1 + (40)(0.6)

= -40/25

结果的方框图现在将显示为

步骤 4： 方框图的传递函数将是

Vo(s)/Vi(s) = -(40/25) x3/ {1 + 40/25 x 3 x 1.5/4)

= (-120/25)/ 2.8

= -120/70

= -1.714