二阶系统的时间响应

在上面的传递函数中，分母中 's' 的幂是 2。这就是为什么上面的传递函数是二阶的，并且该系统被称为二阶系统。

单位阶跃输入下二阶系统的时间响应

根据公式 1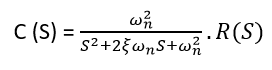

对于单位阶跃，输入为

现在对上述方程进行拉普拉斯逆变换

这个方程也可以写成

二阶系统的瞬态响应指标

控制系统的性能通常用单位阶跃输入的瞬态响应来表示，因为它很容易生成，初始条件基本上为零。

以下是常见的瞬态响应特性

1. 延迟时间。
2. 上升时间。
3. 峰值时间。
4. 最大峰值。
5. 稳定时间。
6. 稳态误差。

延迟时间

响应第一次达到最终值的 50% 所需的时间称为延迟时间。

上升时间

对于过阻尼系统，响应从最终值的 10% 上升到 90% 所需的时间；对于欠阻尼系统，从 0 上升到 100% 所需的时间称为系统的上升时间。

峰值时间

响应达到时间响应的第一个峰值或第一个峰值过冲所需的时间称为峰值时间。

最大过冲

第一个峰值和稳态输出之间的差异称为最大过冲。 它由以下定义：

稳定时间 (t_s)

响应达到并保持在其最终值的指定范围（2% 到 5%）内所需的时间称为稳定时间。

稳态误差 (e_ss)

当时间“t”趋于无穷大时，实际输出和期望输出之间的差异称为系统的稳态误差。

示例 - 1

当一个二阶系统受到单位阶跃输入时，ξ = 0.5 且 ωn = 6 rad/sec。 确定上升时间、峰值时间、稳定时间和峰值过冲。

解决方案

给定-

上升时间

峰值时间

稳定时间

最大过冲