稳定性条件

控制系统的基本要求是它应该具有稳定性。 这意味着系统的输出应该跟随输入。 如果输入是有限的，则输出也需要是有限的，以满足稳定性条件。

一个LTI（线性时不变）系统应在以下条件下保持稳定

1. BIBO（有界输入有界输出）
   这意味着在任何初始条件下，系统对有界输入信号的响应是有界输出信号。 如果满足此条件，则该系统被称为BIBO。 它通常用于信号处理系统。
2. 线性输入和输出，与初始条件无关
   这意味着如果输入为零，则输出也应该为零，而与任何初始条件无关。

让我们考虑两个由以下方程式描述的系统

1. y(t) = x(t)
2. y(t) = {x(t)}^-1

其中，

x(t) = e^-t

这两种情况下的输入均为e^-t（反指数函数）。 下面显示了该图

上述输入是有界输入。 现在，为了满足稳定条件，输出也需要是有界的。 上图显示输出减小并达到值0。因此，系统是稳定的。

让我们考虑一个正指数图的情况。 下面显示了正指数图（Y(t) = e^t）

在这种情况下，输出随时间增加。 它趋于无穷大。 当输出趋于无穷大时，它变得不稳定。

关于极点和零点位置的稳定性

在极点和零点方面，我们可以将传递函数表示为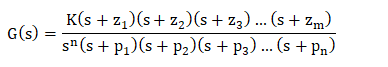

在这里，z代表零点，p代表极点。 使给定传递函数的分子等于零的s值称为系统的零点。 类似地，使给定传递函数的分子等于零的s值称为系统的极点。

分子的根可以表示为？z1，-z2，-z3... -zm，这被称为零点。

分母的根可以表示为？p1，-p2，-p3... -pn，这被称为极点。 极点是传递函数为无穷大的s值。 这是因为它属于分母的一部分。 1/无穷大 = 0。

零点和极点都可以是实数或复数量。

让我们考虑一个例子。

示例：G(s) = (s + 5)(s + 2)/ (s + 1)

在这里，分子中有两项，分母中有一项。 这意味着上述传递函数包括两个零点和一个极点。

令分子为0，

(s + 5)(s + 2) = 0

s = -5, -2

因此，零点为-5和-2。

令分母为0，

(s + 1) = 0

s = -1

因此，极点为-1。

极点和零点显示在下图。

S平面图

s变量等于jw。 这意味着变量s是一个复数。 我们还可以使用s的值来构造一个图。 传递函数提供了可以图形方式绘制的极点和零点。

请考虑以下示例。

示例：G(s) = 5 (s + 2)/ s^2 + 2s + 2

解决方案

可以通过将分子设为0来获得零点。 它由

5 (s + 2) = 0

S = -2

通过将分母设为0可以获得极点。 它由

s^2 + 2s + 2 = 0

求解后，我们得到

-1 + j和-1 -j。

零极点图如下所示

让我们讨论关于极点位置的系统稳定性。

在s平面的左半部分具有负实部的极点被认为是稳定系统的极点。 因此，我们可以说一个稳定的系统具有一个闭环传递函数，该传递函数的极点仅位于s平面的左半部分。

如果一个或多个极点出现在s平面的右半部分或极点位于虚轴上，则该系统是不稳定的。

在开始Routh Hurwitz标准之前，让我们先讨论一下它的一些概念。

Routh Hurwitz标准的基本概念

• Routh标准没有提供特征方程的根的精确位置，这些根位于s平面的右半部分。 这是因为如果任何一个根接近s平面的右半部分，系统就会变得不稳定。
• 它没有说明根是实数还是复数。 实根以实数的形式表示。 复根用iota表示并包括虚部。
• 它仅适用于线性系统。
• 如果特征方程是代数，则该标准有效。 这意味着如果特征方程的任何系数为指数或复数，则该标准无效。