线性时不变 (LTI) 系统的瞬态和稳态分析2025年3月17日 | 阅读 3 分钟 时域响应分析当任何系统的能量状态受到干扰,并且干扰发生在输入端、输出端或两端时,它需要一些时间才能从一个状态变为另一个状态。将状态从一个状态变为另一个状态所需的时间称为瞬态时间,在此期间的电流和电压值称为瞬态响应。 根据系统的参数,瞬态可能具有振荡,其性质可能是持续的或衰减的。 因此,控制系统的时间响应分为两部分:
瞬态响应 它处理系统在受到输入时的响应性质。 稳态分析 它处理输入和输出之间稳态误差大小的估计。 不同类型的标准测试信号 影响系统性能的各种输入或干扰在数学上表示为标准测试信号。
注意
时域分析的特征
瞬态时间:从一个状态变为另一个状态所需的时间称为瞬态时间。 瞬态响应:在此时间变化期间的电流和电压值称为瞬态响应。  因此,我们可以说,瞬态响应是响应的一部分,当时间增加时,它变为零,而稳态响应是总响应的一部分,在瞬态消失之后。如果稳态响应的输出部分与输入不匹配,则系统具有稳态误差。 用于瞬态分析的测试输入信号为了分析控制系统的时间响应,使用以下输入信号。 阶跃函数 单位阶跃函数用 u(t) 表示,定义如下 拉普拉斯变换:  阶跃函数也称为位移函数。如果输入是 R(S),则 R(s) = 1/s 斜坡函数 此函数从原点开始,随时间线性减小或增大,如上图所示。 令 r(t) 为斜坡函数,则 其中 'K' 是直线的斜率,对于 'K' 的正值,斜率向上,对于 'K' 的负值,斜率向下。 拉普拉斯变换  抛物线函数 当 t<0 时,r(t) 的值为零,当 t>0 时,它是时间的二次函数。 其中 'K' 是单位抛物线函数的常数,K = 1。单位抛物线函数定义如下 拉普拉斯变换  脉冲函数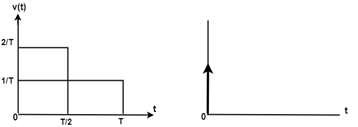 单位脉冲函数定义为  因此,我们可以说,脉冲函数在除 t=0 以外的任何地方都具有零值,其中振幅是无限的。 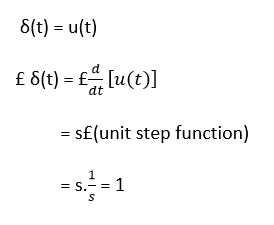 下一主题一阶系统的时间响应 |
我们请求您订阅我们的新闻通讯以获取最新更新。