极坐标图

正弦传递函数的极坐标图是幅值 G(jω) 与 G(jω) 的相位角在极坐标系中的图形。在极坐标图中，频率从零变化到无穷大。极坐标图绘制在极坐标纸上，极坐标纸是一种图纸，由同心圆和径向线组成。

极坐标图上的同心圆代表幅值，径向线代表相位角。图上的每个点都显示了幅值和相位角的信息。

下面是极坐标图的例子

极坐标图中的正角沿逆时针方向测量，而负角沿顺时针方向测量。两个角度都以参考点（即 0 度轴）为基准进行测量。

矩形形式的传递函数 G(jω) 可以写成

G(jω) = GR(jω) + GI(jω)

其中，

G_R(jω) 是传递函数 G(jω) 的实部

G_I(jω) 是传递函数 G(jω) 的虚部

正如前面讨论的，极坐标图中的角频率从零变化到无穷大。我们不应将其与奈奎斯特图混淆，奈奎斯特图是极坐标图的扩展。角频率 (ω) 从零变化到无穷大，而奈奎斯特图的频率范围从负无穷大到正无穷大。

极坐标图的主要优点在于它能在单个图上描绘出系统在整个频率范围内的频率响应特性。由于所有内容似乎都在一个整体中，它无法显示开环传递函数各部分的贡献。

极坐标图的积分因子由以下给出

G(s) = 1/s

其中，

S = jω

s 是传递函数

G(jω) = 1/jω

这是负虚轴。

极坐标图的微分因子由以下给出

G(jω) = jω

这是正虚轴。

添加极点和零点的影响

• 在极坐标图中添加极点会将其末端向负 90 度移动。
• 在极坐标图中添加零点会将其末端向正 90 度移动。

系统类型和阶数

极坐标图中系统的类型决定了极坐标图开始的象限。所有极点的极坐标图的开始图示如下。

极坐标图中系统的阶数决定了极坐标图结束的象限。所有极点的极坐标图的结束图示如下。

标准传递函数的极坐标图

在此，我们将讨论各种标准传递函数的极坐标图。

类型 0

阶数：1

令 G(s) = 1/(1 + sT)

令 s = jω

G(jω) = 1/(1 + jωT)

上述传递函数以幅值和角度形式表示为

G(jω) = 1/[(1 + ω² T²)^1/2∠tan^-1ωT]

如果我们将角度部分放在分子中，由于从分母到分子或反之的转换，我们需要加上一个负号。

G(jω) = 1∠-tan^-1ωT /(1 + ω² T²)^1/2

让我们找出上面函数在零和无穷大处的值。

当 ω = 0 时

G(jω) = 1∠0/1

G(jω) = 1∠0

这是因为 tan^-10 = 0

当 ω = 无穷大时

G(jω) = 0∠-90

这是因为 tan^-1 ∞ = 90 度

零和无穷大处的极坐标图将显示为

阶数 2

由于这是一个二阶系统，该函数包含最高导数变量 (s) 的幂为 2。

令 G(s) = 1/(1 + sT₁) (1 + sT₂)

令 s = jω

G(jω) = 1/(1 + jωT₁) (1 + jωT₂)

上述传递函数以幅值和角度形式表示为

G(jω) = 1/[(1 + ω² T₁ ²)^1/2∠tan^-1ωT₁][(1 + ω² T₂ ²)^1/2∠tan^-1ωT₂]

如果我们将角度部分放在分子中，由于从分母到分子的转换，我们需要加上一个负号，如下所示

G(jω) = 1∠(-tan^-1ωT₁ - tan^-1ωT₂) /(1 + ω² T₁ ²)^1/2(1 + ω² T₂ ²)^1/2

让我们找出上面函数在零和无穷大处的值。

当 ω = 0 时

G(jω) = 1∠(-0 - 0)/1x1

G(jω) = 1∠0

这是因为 tan^-10 = 0

当 ω = 无穷大时

G(jω) = 0∠(-90 - 90)/1

G(jω) = 0∠-180

这是因为 tan^-1 ∞ = 90 度

零和无穷大处的极坐标图将显示为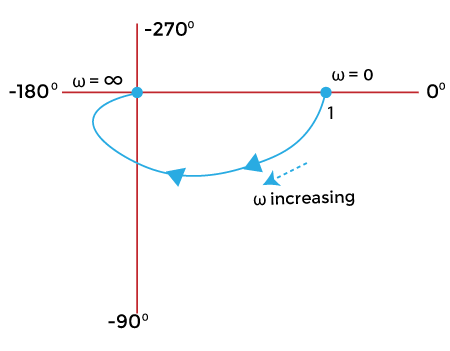

类型 1

阶数：1

令 G(s) = 1/s

令 s = jω

G(jω) = 1/jω

G(jω) = 1/(ω∠90)

如果我们将角度部分放在分子中，由于从分母到分子的转换，我们需要加上一个负号，如下所示

G(jω) =1∠-90 /ω

让我们找出上面函数在零和无穷大处的值。

当 ω = 0 时

G(jω) =∞ ∠-90

这是因为函数直接除以 ω。1/0 = 无穷大。

tan^-10 = 0

当 ω = 无穷大时

G(jω) = 0∠-90

这是因为函数直接除以 ω。1/无穷大 = 零。

tan^-1 ∞ = 90 度

零和无穷大处的极坐标图将显示为

阶数：2

令 G(s) = 1/s(1 + sT)

令 s = jω

G(jω) = 1/ jω(1 + jωT)

上述传递函数以幅值和角度形式表示为

G(jω) = 1/ω∠90 [(1 + ω² T²)^1/2∠tan^-1ωT]

如果我们将角度部分放在分子中，由于从分母到分子或反之的转换，我们需要加上一个负号。

G(jω) = 1∠(-90 - tan^-1ωT) / ω(1 + ω² T²)^1/2

让我们找出上面函数在零和无穷大处的值。

当 ω = 0 时

G(jω) =∞ ∠-90

这是因为函数直接除以 ω。1/0 = 无穷大。

tan^-10 = 0

当 ω = 无穷大时

G(jω) = 0∠(-90-90)

G(jω) = 0∠-180

这是因为函数直接除以 ω。1/无穷大 = 零。

tan^-1 ∞ = 90 度

零和无穷大处的极坐标图将显示为

阶数：3

令 G(s) = 1/s(1 + sT₁) (1 + sT₂)

令 s = jω

G(jω) = 1/ jω (1 + jωT₁) (1 + jωT₂)

上述传递函数以幅值和角度形式表示为

G(jω) = 1/ ω∠90 [(1 + ω² T₁ ²)^1/2∠tan^-1ωT₁][( 1 + ω² T₂ ²)^1/2∠tan^-1ωT₂]

如果我们将角度部分放在分子中，由于从分母到分子的转换，我们需要加上一个负号，如下所示

G(jω) = 1∠(-90 -tan^-1ωT₁ - tan^-1ωT₂) /ω(1 + ω² T₁²)^1/2(1 + ω² T₂²)^1/2

让我们找出上面函数在零和无穷大处的值。

当 ω = 0 时

G(jω) =∞ ∠-90

这是因为函数直接除以 ω。1/0 = 无穷大。

tan^-10 = 0

当 ω = 无穷大时

G(jω) = 0∠(-90 -90 -90)

G(jω) = 0∠-270

这是因为函数直接除以 ω。1/无穷大 = 零。

tan^-1 ∞ = 90 度

零和无穷大处的极坐标图将显示为

类型 2

阶数：4

令 G(s) = 1/s²(1 + sT₁) (1 + sT₂)

令 s = jω

G(jω) = 1/ j² ω² (1 + jωT₁) (1 + jωT₂)

上述传递函数以幅值和角度形式表示为

G(jω) = 1/ ω²∠-180 [(1 + ω² T₁ ²)^1/2∠tan^-1ωT₁][( 1 + ω² T₂ ²)^1/2∠tan^-1ωT₂]

如果我们将角度部分放在分子中，由于从分母到分子的转换，我们需要加上一个负号，如下所示

G(jω) = 1∠(-180-tan^-1ωT₁ - tan^-1ωT₂) /(1 + ω² T₁ ²)^1/2(1 + ω² T₂²)^1/2

让我们找出上面函数在零和无穷大处的值。

当 ω = 0 时

G(jω) = ∞ ∠(-180 - 0 - 0)/1x1

G(jω) = ∞ ∠-180

这是因为函数直接除以 ω。1/0 等于无穷大。

tan^-10 = 0

当 ω = 无穷大时

G(jω) = 0∠(-180 - 90 - 90)/1

G(jω) = 0∠-360

这是因为函数直接除以 ω。1/无穷大 等于零。

tan^-1 ∞ = 90 度

零和无穷大处的极坐标图将显示为

极坐标图的增益裕度和相位裕度

增益裕度是 Kg。它由以下给出

Kg = 1/G_B

G_B 是幅度圆上与 180 度轴相交点的（B）值。如果点 B 位于单位圆内，则增益裕度为正。否则为负。

相位裕度由以下给出

Y = 180 + theta

其中，

Theta 是在增益交叉频率下的 G(jω) 的相位角。当幅度曲线与外部单位圆相交时计算相位角。从该交点到图形末端的线决定了角度 theta。它可以是正的或负的。

借助示例可以更好地理解相位裕度和增益裕度。

示例

让我们讨论一个极坐标图的例子。

示例：单位反馈系统的开环传递函数为 G(s) = 1/s(s + 1)(2s + 1)。绘制极坐标图并确定增益裕度和相位裕度。

解：传递函数由以下给出

G(s) = 1/s(s + 1)(2s + 1)

上述函数清楚地表明该系统是类型 1 阶 3。它具有以下形式

G(s) = 1/s(1 + sT₁) (1 + sT₂)

令 s = jω

G(s) = 1/ jω (jω + 1)(2jω + 1)

上述传递函数以幅值和角度形式表示为

G(jω) = 1/ ω∠90 [(1 + ω²)^1/2∠tan^-1ω][( 1 + ω²4)^1/2∠tan^-1ω2]

如果我们将角度部分放在分子中，由于从分母到分子的转换，我们需要加上一个负号，如下所示

G(jω) = 1∠(-90 -tan^-1ω - tan^-1 2ω) / ω(1 + ω²)^1/2(1 + 4ω²)^1/2

现在，让我们从上面的方程中分离出幅度和角度项。

|G(jω)| = 1/ ω((1 + ω²) (1 + 4ω²))^1/2

|G(jω)| = 1/ ω(1 + 4ω² + ω²+ 4ω⁴)^1/2

|G(jω)| = 1/ ω(1 + 5ω² + 4ω⁴)^1/2

Angle G(jω) = -90 -tan^-1ω - tan^-1 2ω

我们知道上面函数在零和无穷大处的值。

当 ω = 0 时

G(jω) =∞ ∠-90

当 ω = 无穷大时

G(jω) = 0∠-270

让我们找出不同频率下的 G(jω) 的幅值和相位。

极坐标图如下所示

这里，每两条线之间的间隔为15 度。我们指定了点上的正负角度值。这是基于正角度沿逆时针测量，负角度沿顺时针测量的概念。当我们从 0 度角沿顺时针方向开始时，我们可以注意到角度的负值在增加。同样，当我们从 0 度角沿顺时针方向开始时，我们可以注意到角度的正值在上升。

让我们计算增益裕度和相位裕度。

从极坐标图可以看出，幅度圆在点 0.7 处与 180 度轴相交。因此，这将是 G_B 的值。

增益裕度是 Kg = 1/G_B

Kg = 1/0.7

Kg = 1.428

相位裕度由以下给出

Y = 180 + theta

我们可以清楚地看到用红色标记的点。这是幅度曲线与单位圆的交点。从交点（标有红色）绘制的线确定了 theta 角，该角等于 (-168) 度。

因此，相位角等于

Y = 180 - 168

Y = 12 度

因此，增益裕度为 1.428，相位角为 12 度。