根轨迹的例子

在这里，我们将讨论一个根轨迹图的例子。如前所述，我们将遵循根轨迹的六个规则。我们还将讨论在根轨迹上添加极点和零点的影响。

在开始一个例子之前，让我们先讨论一下解决根轨迹问题的步骤。

1. 从给定的传递函数中找到极点、零点、分支数等。
2. 绘制显示标记在其上的极点和零点的图。
3. 计算渐近线的角度并绘制一个单独的草图。
4. 找到质心并绘制一个单独的草图。
5. 找到分离点。这些点也可以用复数的形式表示。我们可以使用角度条件来验证复数形式的这些点。
6. 计算根轨迹与虚轴（或 y 轴）的交点。
7. 如果适用，计算到达和离开的角度。
8. 通过组合以上所有草图绘制根轨迹的最终草图。
9. 我们还可以使用根轨迹技术预测给定系统的稳定性和性能。

大多数步骤可能会令人困惑。让我们讨论一个例子，它将帮助我们了解绘制根轨迹图的方法以及解释。

例子：绘制闭环系统的根轨迹图，其环路传递函数为

G(s)H(s) = K/s(s + 5)(s + 10)

同时找出系统是否稳定。

解决方案：我们将按照上述步骤的步骤进行操作。

步骤 1： 找到极点、零点和分支。

给定传递函数的 Denominator 表示极点，Numerator 表示零点。因此，有 3 个极点，没有零点。

极点 = 0, -5 和 -10

零点 = 无零点

P - Z = 3 - 0 = 3

有三个分支 (P - Z) 趋向无穷大，并且没有开环零点。因此，无穷大将是根轨迹的终止点。

步骤 2： 根轨迹所在的实轴部分。

有三个极点，如下所示

在 0 和 -5 之间（例如，-3.5）的部分在其右侧只有一个极点。这意味着给定点一侧的极点和零点的总和为 1。

规则 3 描述了 0 和 -5 之间的部分位于根轨迹上。类似地，-10 之后的部分也位于根轨迹上。-5 和 -10 之间的部分在右侧有偶数个零点和极点。因此，实轴上 -5 和 -10 之间的根轨迹不存在。

给定系统的分离点将位于根轨迹存在的实轴部分之间，即 0 和 -5。

步骤 3： 渐近线的角度。

此类渐近线的角度由下式给出

= (2q + 1)180 / P - Z

q = 0, 1, 和 2

对于 q = 0,

角度 = 180/3 = 60 度

对于 q = 1,

角度 = 3x180/3 = 180 度

当 q = 2 时，

角度 = 5x180/3 = 300 度

步骤 4： 质心

质心由下式给出

= 0 - 5 - 10 - 0/3

= -15/3

= -5

因此，根轨迹的质心位于实轴上的 -5 处。

显示质心和渐近线角度的图如下所示

步骤 5： 分离点

我们知道，分离点将位于 0 和 -5 之间。让我们找到有效的分离点。

1 + G(s)H(s) = 0

将给定传递函数的值代入上述方程，我们得到

1 + K/s(s + 5)(s + 10) = 0

s(s + 5)(s + 10) + K = 0

s(s² + 15s + 50) + K = 0

s³ + 15s² + 50s + K = 0

K = - s³ - 15s² - 50s

对两边求导，

Dk/ds = - (3s² + 30s + 50) = 0

3s² + 30s + 50 = 0

将等式除以 3，我们得到

s² + 10s + 16.667 = 0

现在，我们将使用公式找到给定方程的根

使用值 a = 1, b = 10, 和 c = 16.667

该方程的根将是 -2.113 和 -7.88。

在这两个根中，只有 -2.113 位于 0 和 -5 之间。因此，这将是分离点。

让我们通过将根的值代入方程 K = - s³ - 15s² - 50s 来验证。

K = - -2.113 ³ - 15(-2.113)² - 50(-2.113)

K = 48.112

发现 K 的值为正数。因此，这是一个有效的分离点。

步骤 6： 与负实轴的交点。

在这里，我们将使用 Routh Hurwitz 准则，使用方程 s³ + 15s² + 50s + K = 0 找到根轨迹在虚轴上的交点

Roth 表如下所示

从第 3 行 s, 750 - K/K = 0

750 - K = 0

K = 750

从第 2 行 s²,

15 s² + K = 0

将 Kin 的值代入上述方程，我们得到

15 s² = -750

s² = -750/15

s² = -50

s = j7.071 和 -j7.071

这两个点都位于正虚轴和负虚轴上。

步骤 7： 给定传递函数中不存在复极点。因此，不需要出发角。

步骤 8： 组合以上所有步骤。

因此，组合以上所有步骤后形成的根轨迹如下所示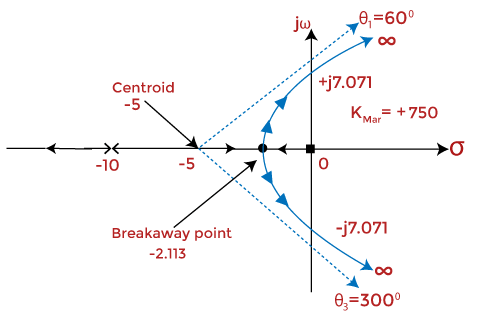

步骤 9： 系统的稳定性

系统可以是稳定的、临界稳定的或不稳定的。在这里，我们将根据上述 Roth Hurwitz 准则确定系统对于不同 K 值的稳定性。

如果 K 的值介于 0 和 750 之间，则系统是稳定的。K 的根轨迹位于 s 平面的左半部分。对于大于 750 的值，系统变得不稳定，这是因为根开始向 s 平面的右半部分移动。但是，在 K = 750 时，系统是临界稳定的。

我们可以得出结论，稳定性基于根在 s 平面的左半部分或右半部分的位置。

添加极点和零点对根轨迹的影响

让我们讨论添加极点和零点对根轨迹的影响。

添加极点的影响

将极点添加到 s 平面的左半部分的影响将把根轨迹推向 s 平面的右侧。我们知道，当根位于 s 平面的左半部分时，系统趋于稳定。当根轨迹向右半部分移动时，稳定性会降低 reduces。 这意味着在根轨迹上添加极点会降低系统的稳定性。系统“K”的范围和增益裕度也会降低。

例如：

考虑系统 G(s)H(s) = K/s(s + 2)(s + 4) 的图。

现在，让我们向上述系统添加 s = -6 极点。根轨迹图现在将显示为

G(s)H(s) = K/s(s + 2)(s + 4)(s + 6)。

我们可以注意到，添加极点导致根轨迹也向 s 平面的右半部分移动。

添加零点的影响

添加零点的影响将把根轨迹推向 s 平面的 左侧。我们知道，当根位于 s 平面的左半部分时，系统趋于稳定。当根轨迹向左半部分移动时，稳定性会提高。这意味着在根轨迹上添加零点将提高系统的稳定性。系统“K”的范围和增益裕度也会增加。

在这里，根轨迹将向添加的零点移动。

例如：

考虑系统 G(s)H(s) = K(s + 4)/s(s + 2)。

现在，让我们向上述系统添加零点 s = -6。根轨迹图现在将显示为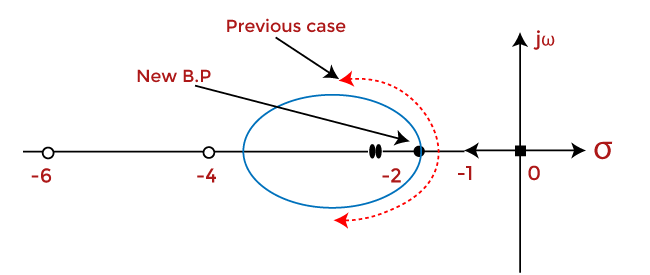

G(s)H(s) = K(s + 4)(s + 6)/s(s + 2)。

我们可以注意到，添加极点导致根轨迹也向 s 平面的右半部分移动。