算法的渐近分析 (函数增长)

算法的资源通常表示为关于输入的函数。通常这个函数很混乱，并且很难处理。为了有效地研究函数增长，我们将函数简化为重要的部分。

  Let f (n) = an2+bn+c

在这个函数中，当 n 足够大时，n² 项控制着该函数。

主导项是我们感兴趣的简化函数的部分，在这种情况下；我们忽略所有常量和系数，并查看关于 n 的最高阶项。

渐近表示法

“渐近”一词表示任意接近某个值或曲线（即，作为某种极限被取走）。

渐近分析

它是一种表示极限行为的技术。该方法在科学领域具有应用。它可用于分析应用于某些大型数据集的算法的性能。

1. 在计算机科学中，在算法分析中，考虑将算法应用于非常大的输入数据集时的性能

最简单的例子是函数 *ƒ (n) = n²+3n*，当 n 非常大时，项 3n 相比于 *n²* 变得微不足道。函数“*ƒ (n)* 被称为与 *n²* **渐近等价**，当 *n → ∞* 时”，这里用符号写为 *ƒ (n) ~ n²*。

**渐近符号**用于编写算法最快和最慢的可能运行时间。这些也分别被称为“最佳情况”和“最坏情况”方案。

“在渐近符号中，我们根据输入的大小推导出复杂度。（例如用 n 表示）”

“这些符号非常重要，因为在不增加运行算法的成本的情况下，我们可以估计算法的复杂度。”

为什么渐近符号很重要？

1. 它们给出了算法效率的简单特征。

2. 它们允许比较各种算法的性能。

渐近记号

渐近符号是一种比较函数的方式，它忽略了常数因子和小的输入大小。使用三个符号来计算算法的运行时间复杂度

**1. 大O符号：** 大O 是表达算法运行时间上限的正式方法。它是衡量最长时间的量度。函数 **f (n) = O (g (n))** [读作 "f of n is big-oh of g of n"] 当且仅当存在正数常数 c 并且存在 n₀ 使得

因此，函数 g (n) 是函数 f (n) 的上限，因为 g (n) 比 f (n) 增长得更快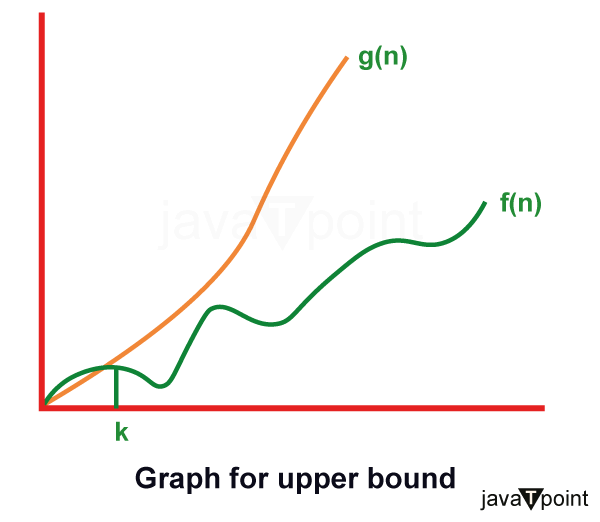

例如

因此，**f(n)** 的复杂度可以表示为 O (g (n))

**2. Omega (Ω) 符号：** 函数 f (n) = Ω (g (n)) [读作 "f of n is omega of g of n"] 当且仅当存在正数常数 c 和 n₀ 使得

F (n) ≥ k* g (n) for all n, n≥ n0

例如

  f (n) =8n2+2n-3≥8n2-3
        =7n2+(n2-3)≥7n2 (g(n))
Thus, k1=7

因此，**f (n)** 的复杂度可以表示为 Ω (g (n))

**3. Theta (θ)：** 函数 f (n) = θ (g (n)) [读作 "f is the theta of g of n"] 当且仅当存在正数常数 k₁、k₂ 和 k₀ 使得

  k1 * g (n) ≤ f(n)≤ k2 g(n)for all n, n≥ n0

例如

3n+2= θ (n) as 3n+2≥3n and 3n+2≤ 4n, for n
    k1=3,k2=4, and n0=2

因此，f (n) 的复杂度可以表示为 θ (g(n))。

Theta 符号比大O和Omega 符号都更精确。如果 g(n) 既是上限又是下限，则函数 f (n) = θ (g (n))。