正则表达式匹配

正则表达式匹配也是经典的动态规划问题之一。

给定一个字符串 S 和一个正则表达式 R，编写一个函数来检查字符串 S 是否与正则表达式 R 匹配。假设 S 只包含字母和数字。

正则表达式由以下组成：

• 字母 A-Z
• 数字 0-9
• '*': 匹配 0 个或多个字符
• '.': 匹配一个字符

让我们通过一个例子来理解。

考虑一个字符串

S = "ABBBAC"

考虑一个正则表达式

R = ".*A*"

现在我们将比较字符串与上述给出的正则表达式。

在正则表达式中，

第一个字符是 '.' 字符。'.' 字符表示它应该匹配任何一个字符。它与字符串中的 'A' 字符匹配。

第二个字符是 '*' 字符。'*' 字符表示它应该匹配 0 个或多个字符，因此它匹配字符串中的 3 个 'B' 字符。

第三个字符是 'A'。'A' 字符与字符串 S 中的 'A' 匹配。

第四个字符是 '*'，它与字符串中的 'C' 字符匹配。

因此，正则表达式的所有字符都与字符串 S 匹配。返回 true。

让我们看另一个例子。

考虑以下字符串。

S = "GREATS"

R = "G*T*E"

现在我们需要比较字符串和正则表达式 R。

正则表达式 R 中的第一个字符 'G' 与字符串 'G' 的第一个字符匹配。

正则表达式中的第二个字符 '*' 与字符串中的 "REA" 匹配。

正则表达式中的第三个字符 'T' 与字符串中的 'T' 匹配。

第四个字符 '*' 与 'S' 字符匹配。

第五个字符，即 'E'，与字符串中的任何字符都不匹配。

因此，我们可以说正则表达式不匹配上面给出的字符串，因此返回 False。

现在让我们看看解决此问题的分步方法。

首先，我们将定义系统状态。

参数

我们将使用两个索引，即 i 和 j，其中：

i: S 的最后一个子串的索引。

j: R 的最后一个子串的索引。

成本函数

我们将定义一个函数 matches(i, j, S, R)；此函数返回 true，如果 S 中以 i 结尾的子串与 R 中以 j 结尾的子串匹配。

第二，我们定义转移。

这里的基本情况是 i=-1, j=-1，返回 true，表示 S 和 R 都为空，并且 S 中的所有字符都与正则表达式 R 匹配。

如果 i>=0 且 j=-1，返回 false，表示 S 中有部分字符与 R 中的字符不匹配。这里 i>=0 表示子串 S 不为空，而 j=-1 表示正则表达式 R 为空。

如果 i=0 且 j>=0，返回 false，表示 R 中有部分字符不匹配。

让我们看看这种方法是如何工作的。

S = ABBBAC

R = .*A*

最初，'i' 指向字符串 S 的最后一个字符，即 C，而 'j' 指向正则表达式的最后一个字符，即 *。

第一种情况：'*' 匹配 S 中的一个字符，即 'C'。在这种情况下，'i' 前进并指向 'A'，而 'j' 将保持在同一位置，指向字符 '*'。

第二种情况：'*' 匹配零个字符。在这种情况下，'i' 将保持在同一位置，而 'j' 前进并指向 A 字符。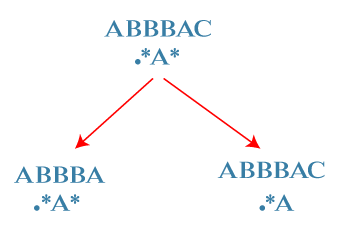

首先，我们将解决左子树。

S = ABBBA

R = .*A*

再次，有两种情况：

要么 '*' 匹配 0 个字符，要么匹配 1 个字符。

第一种情况：'*' 匹配一个字符，即 'A'。在这种情况下，'i' 前进并指向 B，而 'j' 将保持在同一位置，指向 '*'。

第二种情况：'*' 匹配零个字符。在这种情况下，'i' 将保持在同一位置，而 'j' 前进并指向 A 字符。

现在我们将解决右子树。

R 中的 'A' 和 S 中的 'A' 都匹配，因此 'A' 将从 R 和 S 中移除，如下所示：

再次，有两种情况：

S = ABBB

R = .*

第一种情况：'*' 匹配一个字符，即 B。在这种情况下，'i' 前进并指向 B，而 'j' 将保持在同一位置，指向 '*'。

第二种情况：'*' 匹配零个字符。在这种情况下，'i' 将保持在同一位置，我们将 'j' 移到左边。

下一个状态是：

S = ABB

R = .*

第一种状态：'*' 匹配一个字符，即 B。在这种情况下，'i' 前进并指向 B，而 'j' 将保持在同一位置，指向 '*'。

第二种状态：'*' 匹配零个字符。在这种情况下，'i' 将保持在同一位置，我们将 'j' 移到 '*' 的左边。

当我们考虑右子树时，

S = ABBB

R = .

当我们将正则表达式与字符串匹配时，'.' 与 'B' 字符匹配。这意味着 '.' 字符已从正则表达式中移除，变成空。'B' 字符已从字符串 S 中移除，变成 "ABB"。由于正则表达式 'R' 为空，但字符串 'S' 不为空，因此返回 false。

现在我们考虑另一种状态：

S = AB

R = .*

第一种状态：'*' 匹配一个字符，即 B。在这种情况下，'i' 前进并指向 a，而 'j' 将保持在同一位置，指向 '*'。

第二种状态：'*' 匹配零个字符。在这种情况下，'i' 将保持在同一位置，我们将 'j' 移到 '*' 的左边，指向 '.' 字符。

现在我们考虑另一种状态：

S = ABB

R = .

当我们将正则表达式与字符串匹配时，'.' 与 'B' 字符匹配。这意味着 '.' 字符已从正则表达式中移除，变成空。'B' 字符已从字符串 S 中移除，变成 "AB"。由于正则表达式 'R' 为空，但字符串 'S' 不为空，因此返回 false。

现在我们考虑另一种状态：

S = A

R = .*

第一种状态：'*' 匹配一个字符，即 A。在这种情况下，字符串 'S' 将变为空，而 'j' 将保持在同一位置，指向 '*' 字符。由于字符串 S 为空，但正则表达式 'R' 不为空，因此返回 false。

第二种状态：'*' 匹配零个字符。在这种情况下，'i' 将保持在同一位置，我们将 'j' 移到 '*' 的左边，指向 '.' 字符。

现在，我们考虑另一种状态：

S = A

R = .

由于 **R** 中的字符 '.' 与字符串 'S' 中的 'A' 匹配，因此返回 true。现在我们已达到基本情况，即两个字符串都为空并返回 true。一旦返回 true，它将一直传播到顶部，整个解决方案的返回值将为 true。这意味着字符串匹配正则表达式。

3. 转移

基本情况

i = 1 且 j = -1，返回 true，所有字符都匹配，S 和 R 都为空。

i>=0 且 j=-1，返回 false，S 中有部分字符不匹配。

i = -1 且 j>= 0，返回 false，R 中有部分字符不匹配。

R[0: j] = '*'，返回 true，* 匹配 S 中的所有内容。

以下是各种情况：

情况 1

R[j] = S[i]，则

matches(i, j) = matches(i-1, j-1)

情况 2

R[j] = '.'

matches(i, j) = matches(i-1, j-1)

情况 3

R[j] = '*'

如果匹配一个字符，则：

matches(i, j) = matches(i-1, j)

如果匹配零个字符，则：

matches(i, j) = matches(i, j-1 )

在以上两种情况下，只要其中一个函数返回 true，结果就为 true。

递推关系

matches(i, j, S, R) =True, if i = -1 and j = -1 // 表示 S 和 R 都为空。

matches(i, j, S, R) = False, if i = -1 or j = -1 // 表示 S 和 R 均不为空。

matches(i, j, S, R) = matches(i-1, j-1); if S[i] = R[j]

matches(i, j, S, R) = matches(i-1, j-1); if R[j] = .

matches(i, j) = matches(i-1, j) or matches(i, j-1 ), if R[j] = *

让我们看看如何实现 matches() 函数。

4. 记忆化

现在我们将看到如何使用记忆化或自顶向下的方法来实现动态规划。

我们将使用二维数组来缓存或存储结果。这里我们使用 i, j 作为键或参数。

如果字符串 S[0 : i] 与正则表达式 R[0 : j] 匹配，则返回 true。如果子串索引 i 与正则表达式索引 j 匹配，我们将缓存 true 值。

5. 自底向上方法

到目前为止，我们已经看到了自顶向下的方法。现在我们将看到如何使用动态规划来实现自底向上方法。

递推关系

matches(i, j, S, R) = true, if i = -1, j = -1

matches(i, j, S, R) = false, if i = -1, j = -1

matches(i, j, S, R) = matches(i-1, j-1), if S[i] = R[j]

matches(i, j, S, R) = matches(i-1, j-1), if R[j] = .

matches(i, j, S, R) = matches(i-1, j) or matches(i, j-1), if R[j] = *

自底向上方程

Dp[i][j] = true, if i = 0, j=0

Dp[i][j] = false, if i = 0 or j = 0

Dp[i][j] = dp[i-1][j-1], if S[i-1] = R[j-1]

Dp[i][j] = dp[i-1][j-1], if R[j-1] = .

Dp[i][j] = dp[i-1][j] or dp[i][j-1] if R[j-1] = *

让我们实现正则表达式匹配。