旅行商问题

旅行商问题涉及一个销售员和一组城市。销售员必须访问每个城市，从某个城市（例如，家乡）开始，然后返回同一个城市。该问题的挑战在于，旅行销售员需要尽量减少旅行的总长度。

假设城市为 x₁ x₂..... x_n，其中 cost c_ij 表示从城市 x_i 到 x_j 的旅行成本。旅行商问题是要找到一条从 x₁ 开始和结束的路线，该路线将以最小的成本包含所有城市。

示例： 一位报纸代理每天以这样的方式将报纸送到分配的区域：他必须以最小的旅行成本覆盖相应区域内的所有房屋。计算最小的旅行成本。

代理要投递报纸的分配区域如图所示

解决方案：图 G 的成本邻接矩阵如下

cost_ij =

旅行从区域 H₁ 开始，然后选择可从 H₁ 到达的最小成本区域。

标记区域 H₆，因为它是由 H₁ 可达的最小成本区域，然后选择可从 H₆ 到达的最小成本区域。

标记区域 H₇，因为它是由 H₆ 可达的最小成本区域，然后选择可从 H₇ 到达的最小成本区域。

标记区域 H₈，因为它是由 H₈ 可达的最小成本区域。

标记区域 H₅，因为它是由 H₅ 可达的最小成本区域。

标记区域 H₂，因为它是由 H₂ 可达的最小成本区域。

标记区域 H₃，因为它是由 H₃ 可达的最小成本区域。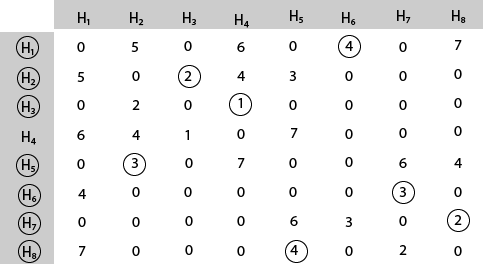

标记区域 H₄，然后选择可从 H₄ 到达的最小成本区域，即 H₁。因此，使用贪婪策略，我们得到以下结果。

4    3    2    4    3    2   1    6
H1 → H6 → H7 → H8 → H5 → H2 → H3 → H4 → H1.

因此，最小的旅行成本 = 4 + 3 + 2 + 4 + 3 + 2 + 1 + 6 = 25

拟阵

拟阵是一个有序对 M(S, I)，满足以下条件

1. S 是一个有限集合。
2. I 是 S 的子集的非空族，称为 S 的独立子集，使得如果 B ∈ I 且 A ∈ I。如果 I 满足此属性，我们说 I 是遗传的。 请注意，空集 ∅ 必然是 I 的成员。
3. 如果 A ∈ I，B ∈ I 且 |A| <|B|，则存在一些元素 x ∈ B ? A，使得 A∪{x}∈I。 我们说 M 满足交换属性。

如果有一个相关的权重函数 w 为每个元素 x ∈ S 分配一个严格正的权重 w (x)，我们说拟阵 M (S, I) 是加权的。 权重函数 w 通过求和扩展到 S 的子集

w (A) = ∑x∈A w(x)

对于任何 A ∈ S。