最大和递增子序列

最大递增子序列和是一个整数列表的子序列，其中和最大，并且子序列中的所有元素都按递增顺序排序。

输出

Maximum sum increasing subsequence is {3, 4, 5}   

让我们再举一个例子来更清楚地理解它。

考虑下面给出的数组

数组：4, 6, 1, 3, 8, 4, 6

在这里，我们考虑三个数组；第一个数组存储数组值，第二个数组存储最大值，第三个数组存储实际序列。

最初，第二个数组存储问题中给出的数组值，第三个数组存储与每个值对应的索引，如下所示。

假设有两个变量，“i”和“j”。对于每个“i”，“j”将一直运行到“i-1”。将“i”处的值与“j”处的值进行比较。

当 i=0, j=0 时

A[i]=4

A[j] = 4

由于“i”和“j”处的值相同，我们将增加“i”的值，“i”的值变为 1。

当 i=1, j =0 时

A[i] = 6

A[j] = 4

由于 A[i] > A[j]，我们将相加“i”和“j”处的值，即 (6+4) 等于 10。我们将用 10 替换第二个数组中 i=1 处的值 6。第三个数组中 i=1 处的索引值 1 被替换为 0，并且“i”的值增加，如下所示。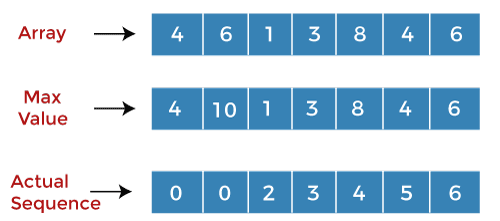

当 i=2, j=0 时

A[i] = 1

A[j] = 4

由于 A[i]

当 i=2，j=1 时

A[i] = 1

A[j] = 6

由于 A[j] > A[i]，因此不会相加，并且“i”的值会增加。“i”的值变为 3，“j”被设置为 0。

当 i=3, j=0 时

A[3] = 3

A[0] = 4

由于 A[j] > A[i]，因此不会相加，并且“j”的值会增加。“j”的值变为 1。

当 i=3, j=1 时

A[3] = 3

A[1] = 6

由于 A[i]

当 i=3, j=2 时

A[3] = 3

A[2] = 1

由于 A[i] > A[j]，我们将相加“i”和“j”处的值，即 (3+1) 等于 4。我们将用 4 替换第二个数组中 i=3 处的值 3。第三个数组中 i=3 处的索引值 3 被替换为 2，并且“i”的值增加，如下所示。

当 i=4, j=0 时

A[4] = 8

A[j] = 4

由于 A[i] > A[j]，我们将相加“i”和“j”处的值，即 (8+4) 等于 12。我们将用 12 替换第二个数组中 i=4 处的值 8。第三个数组中 i=4 处的索引值 4 被替换为 0，并且“j”的值增加，如下所示。

当 i=4, j=1 时

A[4] = 8

A[1] = 6

由于 A[i] > A[j]，我们将相加“i”和“j”处的值。第二个数组中对应于 j 的值为 10，因此我们将相加 (8+10) 等于 18。由于 18>12，因此 12 将在第二个数组的索引 4 处被替换为 18。第三个数组的索引 4 处的值 0 被替换为 1，如下所示。

当 i=4, j=2 时

A[4] = 8

A[2] = 1

由于 A[i]>A[j]，我们将相加“i”和“j”处的值。第二个数组中对应于“j”的值为 1，因此我们将相加 (8+1) 等于 9。值 9 小于值 18，因此不会进行替换。

当 i=4, j=3 时

A[4] = 8

A[3] = 3

由于 A[i]>A[j]，我们将相加“i”和“j”处的值。第二个数组中对应于“j”的值为 4，因此我们将相加 (8+4) 等于 12。值 12 小于值 18，因此不会进行替换。“i”的值增加。

当 i=5, j=0 时

A[5] = 4

A[0] = 4

由于“j”处的值不小于“i”处的值，我们将增加“j”的值。

当 i=5, j=1 时

A[5] = 4

A[1] = 6

由于 A[i] 小于 A[j]，因此“j”的值将增加。

当 i=5, j=2 时

A[5] = 4

A[2] = 1

由于 A[i]>A[j]，我们将相加“i”和“j”处的值。第二个数组中对应于“j”的值为 1，因此我们将相加 (1+4) 等于 5。值 5 大于值 4，因此第二个数组中索引 5 处的值 4 将被替换为 5。第三个数组中索引 5 处的值 5 被替换为 2，如下所示。

当 i=5, j=3 时

A[5] = 4

A[3] = 3

由于 A[i] >A[j]，我们将相加“i”和“j”处的值。第二个数组中对应于“j”的值为 4，因此我们将相加 (4+4) 等于 8。值 8 大于值 5，因此第二个数组中索引 5 处的值 5 将被替换为 8。第三个数组中索引 5 处的值 2 被替换为 3。

当 i=5, j=4 时

A[5] = 4

A[4] = 8

由于 A[j] > A[i]，因此“i”的值增加。“i”的值变为 6，“j”被设置为 0。

当 i=6, j=0 时

A[6] = 6

A[0] = 4

由于 A[i] >A[j]，我们将相加“i”和“j”处的值。第二个数组中对应于“j”的值为 4，因此我们将相加 (4+6) 等于 10。值 10 大于值 6，因此第二个数组中索引 6 处的值 6 将被替换为 10。第三个数组中索引 6 处的值 6 被替换为 0。

当 i=6, j=1 时

A[6] = 6

A[1] = 6

由于 A[6] == A[1]，因此“j”的值增加。“j”的值等于 2。

当 i=6, j=2 时

A[6] = 6

A[2] = 1

由于 A[i] >A[j]，我们将相加“i”和“j”处的值。第二个数组中对应于“j”的值为 1，因此我们将相加 (1+6) 等于 7。值 7 小于值 10，因此不会进行替换。

当 i=6, j=3 时

A[6] = 6

A[3] = 3

由于 A[i] >A[j]，我们将相加“i”和“j”处的值。第二个数组中对应于“j”的值为 4，因此我们将相加 (4+6) 等于 10。计算出的值与第二个数组中索引 6 处的值相同。

当 i=6, j=4 时

A[6] = 6

A[4] = 8

由于 A[j] > A[i]，因此不会进行替换。“j”的值增加并变为 5。

当 i=6, j=5 时

A[6] = 6

A[5] = 4

由于 A[i] >A[j]，我们将相加“i”和“j”处的值。第二个数组中对应于“j”的值为 8，因此我们将相加 (8+6) 等于 14。值 14 大于值 10，因此第二个数组中索引 6 处的值 10 将被替换为 14。第三个数组中索引 6 处的值 0 被替换为 5，如下所示。

正如我们在最大值数组中观察到的，18 是递增子序列的最大和。现在我们将找到构成 18 作为和的子序列中的元素。

对应于 18 的元素是 8；因此，子序列中的第一个元素是 8。

子序列：8

实际序列数组中对应于 18 的值为 1。索引 1 处的值为 6。因此，子序列中的第二个元素是 6。

子序列：6, 8

移动到实际序列数组中的索引 1。索引 1 处的值为 0。数组中的索引 0 处的值为 4。因此，子序列中的第三个元素是 4。

子序列：4, 6, 8

C 语言实现

输出