堆排序

二叉堆

二叉堆是一个可以被视为完全二叉树的数组对象。二叉树的每个节点都对应于数组中的一个元素。

1. 长度 [A]，数组中的元素数
2. 堆大小[A]，在数组A中存储的堆中的元素数。

树 A [1] 的根并给出节点的索引 'i'，可以计算出其父节点、左子节点和右子节点的索引。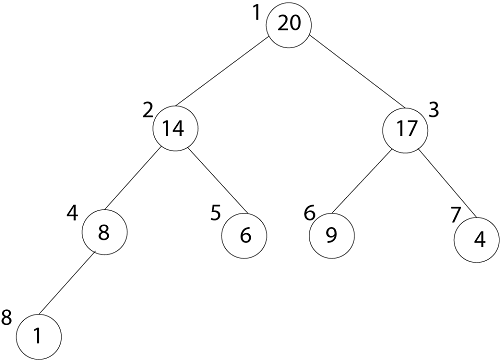

上图的数组表示如下

20 的索引是 1

为了找到左子节点的索引，我们计算 1*2=2

这（正确地）将我们带到 14。

现在，我们向右移动，因此我们计算 2*2+1=5

这（再次正确）将我们带到 6。

现在，4 的索引是 7，我们想转到父节点，因此我们计算 7/2 =3，这会将我们带到 17。

堆属性

二叉堆可以分为最大堆或最小堆

1. 最大堆： 在二叉堆中，对于除根节点以外的每个节点 I，该节点的值大于或等于其最大子节点的值

因此，堆中的最高元素存储在根节点处。以下是 MAX-HEAP 的一个示例

2. 最小堆： 在 MIN-HEAP 中，节点的值小于或等于其最小子节点的值。

堆化方法

1. 维护堆属性： 堆化是用于操作堆数据结构的过程。它给出一个数组 A 和数组的索引 I。以 A [i] 的子节点为根的子树是堆，但节点 A [i] 本身可能违反堆属性，即 A [i] < A [2i] 或 A [2i+1]。过程“堆化”操作以 A [i] 为根的树，使其成为一个堆。

MAX-HEAPIFY (A, i)
 1. l ← left [i]
 2. r ← right [i]
 3. if l≤ heap-size [A] and A[l] > A [i]
 4. then largest ← l
 5. Else largest ← i
 6. If r≤ heap-size [A] and A [r] > A[largest]
 7. Then largest ← r
 8. If largest ≠ i
 9. Then exchange A [i]    A [largest]
 10. MAX-HEAPIFY (A, largest)

分析

一个元素可以向上移动的最大层数是 Θ (log n) 层。在每一层，我们做简单的比较，即 O (1)。因此，堆化的总时间为 O (log n)。

构建堆

BUILDHEAP (array A, int n)
 1 for i ← n/2 down to 1
 2 do
 3 HEAPIFY (A, i, n)

堆排序算法

HEAP-SORT (A)
 1. BUILD-MAX-HEAP (A)
 2. For I ← length[A] down to Z
 3. Do exchange A [1] ←→ A [i]
 4. Heap-size [A] ← heap-size [A]-1
 5. MAX-HEAPIFY (A,1)

分析： 构建最大堆需要 O (n) 的运行时间。堆排序算法调用“构建最大堆”，我们花费 O (n) 时间，并且对 Max-heap 的 (n-1) 次调用以修复一个新的堆。我们知道“Max-Heapify”需要 O (log n) 的时间

堆排序的总运行时间为 O (n log n)。

示例： 在数组上说明 BUILD-MAX-HEAP 的操作。

解决方案：最初

优先队列

与堆一样，优先级队列以两种形式出现：最大优先级队列和最小优先级队列。

优先级队列是一种用于维护一组 S 中元素的 ​​数据结构，每个元素都带有一个称为键的组合值。最大优先级队列引导以下操作

INSERT(S, x): 将元素 x 插入到集合 S 中，这与操作 S=S∪[x] 成正比。

MAXIMUM (S) 返回 S 中具有最高键的元素。

EXTRACT-MAX (S) 移除并返回 S 中具有最高键的元素。

INCREASE-KEY(S, x, k) 将元素 x 的键的值增加到新值 k，该值被认为至少与 x 的当前键值一样大。

让我们讨论如何实现最大优先级队列的操作。过程 HEAP-MAXIMUM 在 θ (1) 时间内考虑 MAXIMUM 操作。

HEAP-MAXIMUM (A)

1. return A [1]

过程 HEAP-EXTRACT-MAX 实现了 EXTRACT-MAX 操作。它类似于堆排序过程的 for 循环。

HEAP-EXTRACT-MAX (A)
 1 if A. heap-size < 1
 2 error "heap underflow"
 3 max ← A [1]
 4 A [1] ← A [heap-size [A]]
 5 heap-size [A] ← heap-size [A]-1
 6 MAX-HEAPIFY (A, 1)
 7 return max

过程 HEAP-INCREASE-KEY 实现了 INCREASE-KEY 操作。数组中的索引 i 标识我们希望增加其键的优先级队列元素。

HEAP-INCREASE-KEY.A, i, key)
 1 if key < A[i]
 2 errors "new key is smaller than current key"
 3 A[i] = key 
 4 while i>1 and A [Parent (i)] < A[i] 
 5 exchange A [i] with A [Parent (i)] 
 6 i =Parent [i]

HEAP-INCREASE-KEY 在 n 个元素的堆上的运行时间为 O (log n)，因为从第 3 行更新的节点到根的路径的长度为 O (log n)。

过程 MAX-HEAP-INSERT 实现了 INSERT 操作。它将要插入到最大堆 A 中的新项目的键作为输入。该过程首先通过计算树到一个新的叶子来扩展最大堆，其键为 - ∞。然后它调用 HEAP-INCREASE-KEY 将此新节点​​的键设置为其正确的值并维护最大堆属性

MAX-HEAP-INSERT (A, key)
 1 A. heap-size = A. heap-size + 1 
 2 A [A. heap-size] = - ∞
 3 HEAP-INCREASE-KEY (A, A. heap-size, key)

MAX-HEAP-INSERT 在 n 个元素的堆上的运行时间为 O (log n)。

示例： 在堆上说明 HEAP-EXTRACT-MAX 的操作

图： HEAP-INCREASE-KEY 的操作

图：(a)

在该图中，最大堆，其索引为“i”的节点被 heavily shaded

图：(b)

在该图中，该节点的键已增加到 15。

图：(c)

在第 4-6 行的 while 循环的一次迭代之后，该节点及其父节点交换了键，并且索引 i 向上移动到父节点。

图：(d)

在 while 循环的另一次迭代之后，A [PARENT (i) ≥A (i)] 最大堆属性现在成立，并且该过程终止。

Heap-Delete

Heap-DELETE (A, i) 是一个过程，它从堆 A 中删除节点“i”中的项目，HEAP-DELETE 在 n 个元素的​​最大堆中以 O (log n) 的时间运行。

HEAP-DELETE (A, i)
 1. A [i] ← A [heap-size [A]]
 2. Heap-size [A] ← heap-size [A]-1
 3. MAX-HEAPIFY (A, i)