Travelling Salesman Problem

引言

旅行商问题 (TSP) 被认为是运筹学和优化领域的基准问题。它体现了现实世界中决策和物流的复杂性，使其在许多不同行业中都具有极高的重要性。该问题最好描述如下：找到一个最短路线，该路线正好访问每个城市一次，然后返回起点城市。尽管旅行商问题的表述简单明了，但其计算复杂性历来引起数学家、计算机科学家和工程师的浓厚兴趣。

历史背景

该问题最早由爱尔兰数学家 W.R. Hamilton 和英国数学家 Thomas Kirkman 在 19 世纪提出。然而，直到 20 世纪中叶，这个问题才开始受到广泛关注。为了解决整数规划问题，George Dantzig、Ray Fulkerson 和 Selmer Johnson 于 1954 年提出了线性规划的概念。这激发了对 TSP 的进一步研究。计算机的发明使得研究人员能够处理更复杂的问题场景，从而催生了多种算法和启发式方法的开发。

什么是旅行商问题？

旅行商问题 (TSP) 是计算机科学和数学领域中一个著名的优化问题。它涉及到确定一条最快的路线，该路线需要精确地访问一组给定的地点一次，然后再返回起点。换句话说，这个挑战在于找到一条路线，使旅行推销员能够在返回出发城市的同时，以最少的旅行时间访问最多的地点。

让我们将一组 n 个城市视为 TSP 的数学表示。目标是找到一个组合，使总的旅行距离最小。通常，距离矩阵用于表示城市之间的距离，其中第 i 行第 j 列的每个条目都表示城市 i 和城市 j 之间的距离。

该问题定义如下：

• 给定 n 个城市及其相应的距离列表。
• 找到一个列表 [city1, city2,..., cityn] 的排列，该排列精确访问每个城市一次，同时使总旅行距离最小。
• 推销员的旅程从同一个城市开始，并在同一个城市结束。

数学公式

TSP 可以用图来数学表示，每个城市作为一个节点，城市之间的距离或旅行成本由节点之间的边表示。目标是找到一个组合，使总旅行距离最小。对于大型案例，穷举搜索非常困难，因为如果 n 个城市，则有 (n-1)! 种可能的路线需要考虑。

旅行商问题的伪代码

此伪代码使用二维数组“distanceMatrix”表示城市之间的距离，其中“distanceMatrix[i][j]”是城市 i 和城市 j 之间的距离。“startingCity”表示推销员行程的起始城市。该算法重复地从当前城市选择最近的未探索城市，并将其添加到行程中，直到访问完所有城市。最后返回一个列表作为行程。

请记住，最近邻算法是一种简单的启发式方法，不一定能保证旅行商问题的最优解。在距离矩阵不满足三角不等式性质的情况下，它可能会导致次优解。此伪代码提供了一种方法的简单概述，但有更复杂的方法和策略可以寻求更好的答案。

复杂度和近似

旅行商问题 (TSP) 是 NP-hard 问题，这意味着没有一种单一的有效方法可以处理所有情况。随着城市数量的增加，其复杂性呈指数级增长，因为 n 个城市有 (n-1)! 种潜在的解决方案。近似算法，例如 Christofide 的方法（对度量 TSP 具有 3/2 的近似度），旨在高效地找到接近最优值的解决方案。尽管这些启发式方法提供了有用的解决方案，但 TSP 仍然是理论复杂性和实际优化交叉点上的一个难题。

基于旅行商问题的分支定界法示例

问题

使用以下图的分支定界算法解决旅行商问题。

解决方案

步骤 1

编写后，降低初始成本矩阵。

规则

• 独立地对矩阵进行行约简和列约简以减小它。
• 如果一行或一列至少有一个“0”项，则认为它已约简。

行约简

考虑以上矩阵中的每一行。

如果行中已存在“0”项，则

• 无需执行此操作。

如果行中缺少“0”项，则

• 约简该特定行。
• 选择该行中值最小的元素。
• 从该行中的每个元素中减去该最小元素。
• 这将通过添加“0”项来约简该行。

之后是。

• 将第 1 行的元素减少 4。
• 第 2 行的元素应减少 5。
• 将第 3 行的元素减少 6。
• 第 4 行的元素应减少 2。

通过这样做，我们得到以下行约简矩阵：

列约简

考虑以上行约简矩阵中的每一列。

如果列中已存在“0”项，则

• 该列无需约简。

如果列中不存在“0”项，则

• 约简该特定列。
• 选择该列中值最小的元素。
• 将该最小元素加到该列的每个元素上。
• 这将通过在该列中添加一个值为“0”的项来约简该列。

此后，我们得到：

• 第 1 列无需约简。
• 第 2 列无需约简。
• 第 3 列的元素应减少 1。
• 第 4 列无需约简。

因此，我们得到后续的列约简矩阵：

原始距离矩阵最终完全约简。

现在，我们加总所有约简的元素以确定节点 1 的成本。

节点 (1) 的成本

所有约简元素的总和

4 + 5 + 6 + 2 + 1

= 18

步骤 2

• 我们考虑每个额外的顶点。
• 为了降低行程成本，我们选择我们可以到达的最佳顶点。

选择前往顶点 B

节点 2 路径 (A → B)

• 在第一个约简矩阵步骤中，M[A,B] = 0；将第 A 行和第 B 列设置为 ∞。
• 将 M[B,A] 设置为 ∞。

由此产生的成本矩阵如下：

现在，

• 此矩阵已约简。
• 之后，我们将找到节点 2 的成本。

行约简

• 由于第 1 行的所有元素都为 ∞，我们无法对其进行约简。
• 将第 2 行的元素减少 13。
• 第 3 行无需约简。
• 第 4 行无需约简。

通过这样做，我们得到以下行约简矩阵：

列约简

• 第 1 列的元素应减少 5。
• 由于第 2 列的所有组件都为 ∞，我们无法对其进行约简。
• 第 3 列无需约简。
• 第 4 列无需约简。

因此，我们得到后续的列约简矩阵：

矩阵最终完全约简。

我们现在正在计算节点 2 的成本。

节点 2 的成本

节点 1 的成本 + 约简元素的总和 + M[A,B]

18 + (13 + 5) + 0

=36

选择前往顶点 C

节点 3 路径 (A → C)

M[A, C] = 7 是从第一个约简矩阵步骤中得出的。

将第 A 行和第 C 列设置为 ∞。

将 M[C, A] 设置为 ∞。

由此产生的成本矩阵如下：

现在，

• 此矩阵已约简。
• 之后，我们将找出节点 3 的成本。

行约简

• 由于第 1 行的所有元素都为 ∞，我们无法对其进行约简。
• 第 2 行无需约简。
• 第 3 行无需约简。
• 第 4 行无需约简。

矩阵已完成行约简。

• 第 1 列的约简不是必需的。
• 第 2 列的约简不是必需的。
• 第 3 列的所有元素都为 ∞。因此，我们无法对其进行约简。
• 第 4 列的约简不是必需的。

因此，矩阵已完成列约简。

矩阵最终完全约简。

我们现在正在计算节点 3 的成本。

节点 2 的成本

节点 1 的成本 + 约简元素的总和 + M[A,B]

18 + 0 + 7

= 25

选择前往顶点 D

节点 4 路径 (A → D)

M[A, D] = 3 是从第一个约简矩阵步骤中得出的。

将第 A 行和第 D 列设置为 ∞。

将 M[D, A] 设置为 ∞。

由此产生的成本矩阵如下：

现在，

• 此矩阵已约简。
• 之后，我们将找出节点 4 的成本。

行约简

由于第 1 行的所有元素都为 ∞，我们无法对其进行约简。

第 2 行无需约简。

将第 3 行的所有元素减少 5。

第 4 行无需约简。

通过这样做，我们得到以下行约简矩阵：

列约简

• 第 1 列的约简不是必需的。
• 第 2 列的约简不是必需的。
• 第 3 列的约简不是必需的。
• 由于第 4 列的所有元素都为 ∞，我们无法约简它。

矩阵已完成列约简。

矩阵最终完全约简。

我们现在正在计算节点 4 的成本。

节点 (4) 的成本

节点 (1) 的成本 + 约简元素的总和 + M[A,D]

18+5+3

= 26

所以，这里我们有：

• 节点 (2) 的成本 = 36 (路径 A→B)
• 节点 (3) 的成本 = 25 (路径 A→C)
• 节点 (4) 的成本 = 26 (路径 A→D)

选择成本最低的节点。

我们选择访问节点 3，因为它成本最低。

因此，我们选择节点 3，或路径 A→ C。

步骤 3

我们分析节点 3 的顶点 B 和 D。

现在，我们从节点 3 的成本矩阵开始，该矩阵是：

选择前往节点 B

节点 5 路径 (A → C → D)

M[C, B] = ∞ 是从第一个约简矩阵步骤中得出的。

将第 C 行和第 B 列设置为 ∞。

将 M[B, A] 设置为 ∞。

由此产生的成本矩阵如下：

此矩阵已约简。

之后，我们将找出节点 5 的成本。

行约简

• 由于第 1 行的所有元素都为 ∞，我们无法对其进行约简。
• 第 2 行需要减少 13。
• 由于第 3 行的所有元素都为 ∞，我们无法对其进行约简。
• 第 4 行需要减少 8。

通过这样做，我们得到以下行约简矩阵：

列约简

• 第 1 列的约简不是必需的。
• 由于第 2 行的所有元素都为 ∞，我们无法对其进行约简。
• 由于第 3 行的所有元素都为 ∞，我们无法对其进行约简。
• 第 4 列的约简不是必需的。

矩阵已完成列约简。

矩阵最终完全约简。

我们现在正在计算节点 5 的成本。

节点 (5) 的成本

节点 (3) 的成本 + 约简元素的总和 + M[C,B]

25 + (13 + 8) + ∞

= ∞

选择前往节点 D

节点 6 路径 (A → C → D)

M[C, B] = ∞ 是从第二个约简矩阵步骤中得出的。

将第 C 行和第 D 列设置为 ∞。

将 M[D, A] 设置为 ∞。

由此产生的成本矩阵如下：

此矩阵已约简。

之后，我们将找出节点 6 的成本。

行约简

• 由于第 1 行的所有元素都为 ∞，我们无法对其进行约简。
• 第 2 行无需约简。
• 由于第 3 行的所有元素都为 ∞，我们无法对其进行约简。
• 由于第 4 行的所有元素都为 ∞，我们无法对其进行约简。

因此，矩阵已完成行约简。

列约简

• 第 1 列的约简不是必需的。
• 由于第 2 行的所有元素都为 ∞，我们无法对其进行约简。
• 由于第 3 行的所有元素都为 ∞，我们无法对其进行约简。
• 由于第 4 行的所有元素都为 ∞，我们无法对其进行约简。

矩阵已完成列约简。

矩阵最终完全约简。

我们现在正在计算节点 6 的成本。

节点 (6) 的成本

节点 (3) 的成本 + 约简元素的总和 + M[C,D]

25 + 0 + 0

= 25

所以，这里我们有：

• 节点 (5) 的成本 = ∞ (路径 A→C→B)
• 节点 (6) 的成本 = 25 (路径 A→C→D)

选择成本最低的节点。

我们选择访问节点 6，因为它成本最低。

因此，我们选择节点 6，或路径 A→C→D。

步骤 4

我们从顶点 B 分析节点 6。

现在，我们从节点 6 的成本矩阵开始，该矩阵是：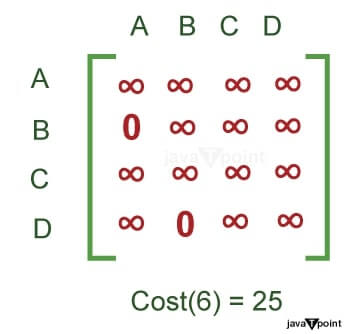

选择前往节点 B

节点 7 路径 (A → C → D → B)

M[D, B] = 0 是从第三个约简矩阵步骤中得出的。

将第 B 行和第 B 列设置为 ∞。

将 M[B, A] 设置为 ∞。

由此产生的成本矩阵如下：

此矩阵已约简。

之后，我们将找出节点 7 的成本。

行约简

• 由于第 1 行的所有元素都为 ∞，我们无法对其进行约简。
• 由于第 2 行的所有元素都为 ∞，我们无法对其进行约简。
• 由于第 3 行的所有元素都为 ∞，我们无法对其进行约简。
• 由于第 4 行的所有元素都为 ∞，我们无法对其进行约简。

矩阵已完成行约简。

列约简

• 由于第 1 列的所有元素都为 ∞，我们无法对其进行约简。
• 由于第 2 列的所有元素都为 ∞，我们无法对其进行约简。
• 由于第 3 列的所有元素都为 ∞，我们无法对其进行约简。
• 由于第 4 列的所有元素都为 ∞，我们无法对其进行约简。

矩阵已完成列约简。

矩阵最终完全约简。

所有条目都变成了 ∞。

我们现在正在计算节点 7 的成本。

节点 (7) 的成本

节点 (6) 的成本 + 约简元素的总和 + M[D,B]

25 + 0 + 0

= 25

最终，

最优路径是 A → C → D → B → A。

路径的总成本为 25 个单位。

C++ 代码实现

输出

Enter the number of cities: 5
Enter the coordinates of each city (x y):
0 0
2 4
5 1
3 3
1 2
Optimal Tour Order:
0 4 1 3 2
Total Distance Travelled: 13.8138

• 此 Java 代码实现了最近邻算法来解决旅行商问题 (TSP)。
• 它首先定义了一个“Point”类来表示城市坐标，以及一个“distance”方法来计算城市之间的距离。
• “nearestNeighborTSP”函数在每个阶段选择最近的未探索城市来确定最佳路线。
• 该程序为一组指定的城市提供了最佳行程顺序和总里程，作为 TSP 解决方案的示例。
• 该代码展示了最近邻算法在处理 TSP 实例时的有效性，使其适用于与现实世界路线规划和优化相关的问题。

Java 代码实现

输出

Optimal Tour Order:
0 4 1 3 2
Total Distance Traveled: 13.8138

• 此 Java 代码实现了最近邻算法来解决旅行商问题 (TSP)。
• 它首先定义了一个“Point”类来表示城市坐标，以及一个“distance”方法来计算城市之间的距离。
• “nearestNeighborTSP”函数在每个阶段选择最近的未探索城市来确定最佳路线。
• 该程序为一组指定的城市提供了最佳行程顺序和总里程，作为 TSP 解决方案的示例。
• 该代码展示了最近邻算法在处理 TSP 实例时的有效性，使其适用于与现实世界路线规划和优化相关的问题。

输出

Optimal Tour Order:
0 4 1 3 2 
Total Distance Traveled: 13.8138

Python 代码实现

• 最近邻算法用于解决旅行商问题 (TSP)。
• 它包括一个用于城市坐标的“Point”类和一个用于计算城市之间距离的“distance”方法。
• “nearest_neighbor_tsp”函数通过从当前城市迭代选择最近的未探索城市来获得最佳行程。
• 它维护一个已访问列表来标记已访问的城市，以及一个行程列表来跟踪访问地点的顺序。
• 该程序为一组城市提供了最佳“行程”顺序和总里程，作为 TSP 解决方案的示例。
• 该代码展示了最近邻算法在处理 TSP 实例时的有效性。

输出

[0, 4, 1, 3, 2]
Total Distance Traveled: 13.81379615571165

TSP 的算法和启发式方法

1. 最近邻算法：这个简单的启发式方法通过从给定城市开始，重复选择最近的未访问城市来创建行程。虽然易于使用，但此策略可能无法始终产生最佳结果。
2. 贪婪算法：与最近邻算法类似，贪婪方法不断地从当前城市选择到未访问城市的边，并选择最短的边。这种方法可以产生接近最优解的结果，但不能保证全局最优。
3. Christofides 算法：该算法于 1976 年创建，它保证对于度量 TSP 的情况，解决方案将不超过最佳解决方案的 3/2 倍。它通过结合最小生成树和一些额外的步骤来创建行程。
4. 遗传算法：遗传算法受自然选择的启发，它创建候选解决方案的种群，并通过选择、交叉和变异等操作反复演化它们。它们通常在大型实例上表现良好，但不能保证始终找到最优解。
5. 蚁群优化： ACO 算法模仿蚂蚁寻找食物的方式，利用信息素路径来指导搜索过程。这种策略已成功地为 TSP 情况找到了合理的解决方案。
6. 模拟退火：这种优化方法借鉴了冶金学的思想，它通过迭代地“冷却”系统，使其能够逃离局部最优并向全局最优移动。

TSP 的应用

旅行商问题 (TSP) 本质上是关于路线优化的，在许多不同的行业中有广泛的实际应用。以下是一些重要的例子：

1. 物流和供应链管理：快递服务、货运公司和供应链管理经常使用 TSP 来优化配送路线。通过缩短旅行距离，可以降低燃料成本和交付时间。
2. 车辆路线规划：拥有车队的业务，如公共交通、垃圾处理和校车服务，利用 TSP 来规划其车辆的高效路线，以确保及时服务和优化资源。
3. 制造和生产：TSP 有助于确定制造工厂中的哪些设备应首先进行检查，从而优化生产计划并减少停机时间。
4. 遗传学和 DNA 测序：TSP 在 DNA 测序中有应用，因为它可以帮助找到测序 DNA 片段的最快和最便宜的方法。
5. 电信：在电信领域，路由和网络架构至关重要。TSP 可用于通过降低延迟和优化数据传输路径来提高网络性能。
6. 医疗保健：TSP 可用于医疗保健行业，以有效安排家庭医疗访问和优化医疗用品的配送路线。
7. 游戏和谜题：在娱乐数学中，找到穿过一系列点的最短路径是一个常见的问题，并且是受 TSP 启发的许多游戏和谜题中的挑战。
8. 机器人路径规划：TSP 在机器人领域用于设计高效的机器人路线，确保它们能够到达特定区域，同时最大限度地减少能源消耗和旅行时间。
9. 军事行动：在需要最小化旅行时间和危险的军事行动（如侦察任务或物资配送）的规划中，TSP 可以提供帮助。

总而言之，旅行商问题是解决各个领域和应用中的路线规划、排序和资源分配问题的宝贵工具。由于其解决这些问题的能力，它已成为运筹学、物流和计算机科学领域的经典概念。

TSP 的空间复杂度

在空间方面，所选择的算法和数据结构对解决旅行商问题 (TSP) 的难度有重大影响。精确算法可能会产生高空间复杂度，因为它们可能需要大量内存来存储中间结果。相比之下，启发式和近似技术通常对大型问题实例具有较低的内存需求。

TSP 的时间复杂度

旅行商问题 (TSP) 的时间复杂度通常是指数级的，最坏情况下的复杂度为 O(n!)，其中 'n' 是城市的数量。这表明随着城市数量的增加，需要考虑的潜在路径数量呈阶乘增长，使得精确解在许多情况下变得不可行。另一方面，启发式和近似算法提供了更有效但次优的解决方案，其时间复杂度通常在 O(n²) 到 O(n³) 之间，具体取决于技术。由于 TSP 本身的计算复杂性，对于大型数据集来说，找到最优解仍然是一个挑战，这凸显了对有用近似方法的需求。

旅行商问题的优缺点

旅行商问题 (TSP) 是一个著名的优化问题，引起了学术界和业界的极大兴趣。这个挑战的目标是找到一条最快的路线，该路线访问集合中的每个城市一次，然后返回起点。尽管 TSP 是一个基本且灵活的问题，但它既有优点也有缺点。

TSP 的优点

1. 现实世界相关性

TSP 在各个行业中有许多现实世界的应用。它在运输、制造和电信等行业中非常适用，因为它模拟了许多现实世界的物流、路线规划和调度难题。

2. 优化潜力

解决 TSP 可以带来显著的成本节约和生产力提高。例如，一家快递公司可以通过确定最短的配送路线来节省成本，从而减少燃料消耗和行程时间。

3. 数学抽象

运筹学和组合优化都将 TSP 作为基本问题。它提供了一个平台来创建和测试可用于解决各种优化问题的启发式方法和算法。

4. 算法研究

TSP 对算法设计和分析研究产生了重大影响。为了更好地理解优化过程，研究人员开发了从精确方法到近似技术的各种算法。

5. 教育和培训

TSP 作为算法概念和问题解决技术的教学工具。它经常在计算机科学和数学课程中用于向学生介绍优化和算法构建。

6. 跨学科见解

工程、计算机科学、运筹学、数学等领域的 TSP 研究都有涉及。不同领域的专业人士之间的合作产生了对各种问题的深刻见解和开创性解决方案。

7. 全球网络

TSP 汇聚了来自世界各地的研究人员和从业人员。通过与 TSP 相关的学术会议、竞赛和合作，促进了优化和算法开发领域专家之间的国际交流。

8. 决策支持

在现实世界的场景中，解决 TSP 可以通过揭示资源分配和路线规划方面的有价值信息来辅助决策。它支持明智的决策，从而降低成本并提高运营效率。

TSP 的缺点

1. 计算复杂度

TSP 的计算复杂度是其主要缺点之一。随着城市数量的增加，该问题的求解时间呈指数级增长。对于大型案例，精确方法通常变得不切实际。

2. NP-Hardness

TSP 被归类为 NP-hard 问题，这意味着不存在一个多项式时间算法可以完美地解决所有可能的输入。这种困难限制了实际获得精确解决方案的可能性。

3. 启发式依赖性

启发式和近似算法提供了可行的答案，但不能保证最优结果。解决方案的正确性很难判断，因为它取决于问题实例和所使用的启发式方法。

4. 对输入数据的敏感性

输入数据，特别是城市的位置和距离，可能对 TSP 的最优解决方案产生重大影响。数据的微小变化可能会对路线长度产生重大影响，从而影响解决方案的可靠性。

5. 内存需求

大型 TSP 案例的精确方法有时需要大量内存来保留中间结果，这可能是一个问题，尤其是在资源有限的系统上。

6. 对问题变体的依赖性

TSP 有多种形式，包括度量 TSP、非对称 TSP 和时间依赖 TSP。没有一种放之四海而皆准的解决方案，因为算法和启发式方法的适用性取决于具体的问题变体。

7. 缺乏并行性

TSP 的本质上顺序的性质使其不太适合并行化，因此在这些系统中对其进行有效求解仍然是一个挑战。

8. 没有通用的算法

尽管进行了大量研究，但没有一种算法或方法能够始终在所有 TSP 案例中胜过其他所有算法。挑战的特性和范围通常会影响所选算法。

结论

旅行商问题的理论挑战和实际影响继续吸引着学者和从业人员。由于处理能力的不断提高和创新的算法技术，在处理更大的 TSP 实例和为各种应用找到可行的解决方案方面正在取得进展。无论是优化配送路线、指导 DNA 测序还是构建高效的网络，TSP 仍然是数学、计算机科学和物流交叉领域的一个经典问题。