如何解决动态规划问题？

什么是动态规划？

动态规划是一种优化技术，由Richard Bellman在20世纪50年代开发。基本上，动态规划是对普通递归的优化。在递归的情况下，会为同一个子问题进行重复调用，但我们可以使用动态规划来优化这个问题。使用动态规划的思想是，我们存储子问题的结果，这样就不需要在需要时重新计算子问题。这可以将时间复杂度从指数级降低到线性级。

下面是具有指数级时间复杂度的递归代码。

下面是具有线性时间复杂度的动态规划代码。

解决动态规划问题的技术。

要解决任何动态规划问题，我们可以使用FAST方法。

在这里，FAST代表

• 'F' 代表 寻找递归解： 无论何时遇到DP问题，我们都需要找到递归解。
• 'A' 代表 分析解： 一旦找到递归解，我们就必须分析该解并寻找重叠问题。
• 'S' 代表 保存结果以供将来使用： 一旦找到重叠问题，我们就存储这些子问题的解决方案。为了存储解决方案，我们使用n维数组进行缓存。

以上三个步骤用于自顶向下方法，如果我们使用“F”、“A”和“S”，这意味着我们实现了自顶向下方法。但这并不完全是，因为我们使用了递归技术。

• 'T' 代表 调整解决方案 以通过消除递归开销使其更强大，这被称为自底向上方法。在这里，我们消除了递归技术，并使用迭代方法来实现相同的结果，所以这是一种纯粹的方法。递归总是一个开销，因为它有可能导致堆栈溢出错误，所以我们应该使用自底向上方法来避免这个问题。

以上是解决复杂问题的四个步骤。

问题陈述：编写一个高效的程序来查找第n个斐波那契数？

众所周知，斐波那契数列看起来像

0, 1, 1, 2, 3, 5, 8, 13, 21,...

首先，我们找到递归解，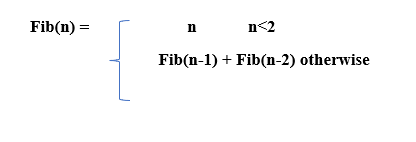

以下是上述递归解的代码

上述递归解也是上述问题的解决方案，但此时的时间复杂度为 O(2ⁿ)。因此，动态规划用于将时间复杂度从指数级降低到线性级。

第二步是分析解

假设我们要计算 fib(4)。

Fib(4)= fib(3) + fib(2)

Fib(3) = fib(2) + fib(1)

Fib(2) = fib(1) + fib(0)

正如我们在上图中所观察到的，fib(2) 被计算了两次，而 fib(1) 被计算了三次。因此，在这里出现了重叠问题。在此步骤中，我们分析了解决方案。

第三步是保存结果。

保存结果的过程称为记忆化。在此步骤中，我们将遵循相同的方法，即递归方法，但有一个小的不同之处在于我们使用了缓存来存储解决方案，以便在需要时可以重复使用。.

以下是记忆化代码。

在上面的代码中，我们使用了大小为 n+1 的缓存数组。如果 cache[n] 不等于零，则从缓存中返回结果；否则，我们将计算 cache 的值，然后返回 cache。我们在这里使用的技术是自顶向下方法，因为它遵循递归方法。在这里，我们总是查找缓存，因此缓存将按需填充。假设我们要计算 fib(4)，首先我们在缓存中查找，如果值不在缓存中，则计算该值并将其存储在缓存中。

上述代码的可视化表示为

第四步是调整解决方案

在此步骤中，我们将完全消除递归，并将其改为迭代方法。因此，这种技术称为自底向上方法。

在上面的代码中，我们遵循了自底向上的方法。我们声明了一个大小为 n+1 的缓存数组。基本情况是 cache[0] 和 cache[1]，其值为 0 和 1。在上面的代码中，我们完全消除了递归。我们使用了一种迭代方法。我们声明了一个 for 循环，其中我们从索引 i=2 到 n 填充缓存，并从缓存中返回结果。假设我们要计算 f(4)，我们首先计算 f(2)，然后计算 f(3)，最后计算 f(4) 的值。我们是从下往上走的，所以这种方法被称为自底向上方法。

我们可以通过图表来可视化这种方法

正如我们在上图中观察到的，我们是从下往上填充缓存的，所以它被称为自底向上方法。这种方法比之前的方法效率更高，因为它不使用递归，但这两种方法具有相同的时间和空间复杂度，即 O(n)。

在这种情况下，我们使用了FAST方法来获得最优解。以上是我们到目前为止获得的最优解，但这并非完全是最优解。

高效解决方案

上述解决方案是高效解决方案，因为我们没有使用缓存。