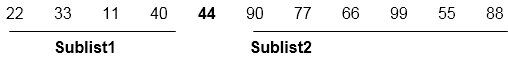快速排序

它是一种分治算法。

分割：重新排列元素并将数组分成两个子数组和一个中间元素，搜索左子数组中的每个元素是否小于或等于平均元素，并且右子数组中的每个元素是否大于中间元素。

征服：递归地对两个子数组进行排序。

合并：合并已排序的数组。

算法

分区算法

分区算法在原地重新排列子数组。

图：显示分区算法的执行轨迹

快速排序的例子

令 44 为 枢轴 元素，并从右向左进行扫描

将 44 与右侧元素进行比较，如果右侧元素 小于 44，则交换它们。由于 22 小于 44，因此交换它们。

  22	33	11	55	77	90	40	60	99	44	88	

现在将 44 与左侧元素进行比较，并且该元素必须 大于 44，然后交换它们。由于 55 大于 44，因此交换它们。

22	33	11	44	77	90	40	60	99	55	88

递归地重复步骤 1 和步骤 2，直到我们得到两个列表，一个来自枢轴元素 44 的左侧，一个来自枢轴元素的右侧。

22	33	11	40	77	90	44	60	99	55	88

与 77 交换

22	33	11	40	44	90	77	60	99	55	88

现在，右侧和左侧的元素分别大于和小于 44。

现在我们得到了两个已排序的列表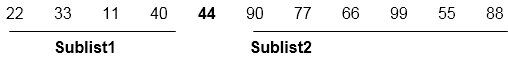

这些子列表是按照与上面相同的过程进行排序的。

这两个已排序的子列表并排显示。

合并子列表

                          已排序的列表

最坏情况分析：当项目已经按排序形式排序，而我们又试图对它们进行排序时就是这种情况。这将花费大量的时间和空间。

方程

T (1) 是枢轴元素所花费的时间。

T (n-1) 是除枢轴元素之外的其余元素所花费的时间。

N：识别其自身的确切位置（每个元素）所需的比较次数

如果我们将第一个元素枢轴与其他元素进行比较，则将进行 5 次比较。

这意味着如果有 n 个项目，则将进行 n 次比较。

最坏情况的关系公式

注意：为了使 T (n-4) 变为 T (1)，我们将用 '4' 替换 (n-1)，并且如果
我们用 (n-1) 替换 4，那么我们必须用 (n-2) 替换 3，用 (n-3)
替换 2，依此类推。

T(n)=(n-1) T(1) + T(n-(n-1))+(n-(n-2))+(n-(n-3))+(n-(n-4))+n
T (n) = (n-1) T (1) + T (1) + 2 + 3 + 4+............n
T (n) = (n-1) T (1) +T (1) +2+3+4+...........+n+1-1

[添加 1 并减去 1 以创建 AP 系列]

T (n) = (n-1) T (1) +T (1) +1+2+3+4+........ + n-1
T (n) = (n-1) T (1) +T 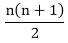(1) + -1

停止条件：T (1) =0

因为最后只剩下一个元素，并且不需要进行比较。

T (n) = (n-1) (0) +0+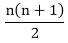-1

快速排序的最坏情况复杂度为 T (n) =O (n²)

随机快速排序 [平均情况]

通常，我们假设列表的第一个元素为枢轴元素。在平均情况下，获得枢轴元素的机会数量等于项目的数量。

因此，一般来说，如果我们将 Kth 元素作为枢轴元素。

然后，

枢轴元素将进行 n 次比较，并且我们正在处理平均情况，因此，

因此，随机快速排序的关系公式为

    = n+1 +(T(0)+T(1)+T(2)+...T(n-1)+T(n-2)+T(n-3)+...T(0))

    = n+1 +x2 (T(0)+T(1)+T(2)+...T(n-2)+T(n-1))

在等式 1 中设 n=n-1

从等式 1 和等式 2

n T (n) - (n-1) T (n-1)= n(n+1)-n(n-1)+2 (T(0)+T(1)+T(2)+?T(n-2)+T(n-1))-2(T(0)+T(1)+T(2)+...T(n-2))
n T(n)- (n-1) T(n-1)= n[n+1-n+1]+2T(n-1)
n T(n)=[2+(n-1)]T(n-1)+2n
n T(n)= n+1 T(n-1)+2n

在等式 3 中设 n=n-1

在等式 3 中代入 4 等式

在等式 3 中设 n=n-2

在等式 5 中代入 6 等式

在等式 3 中设 n=n-3

在等式 7 中代入 8 等式

从 3 等式、5 等式、7 等式、9 等式我们得到

从 10 等式

将最后一项乘以 2 并除以 2

是用于对 n 个元素进行排序的快速排序的平均情况复杂度。

3. 快速排序 [最佳情况]：在任何排序中，最佳情况是我们不对元素进行任何比较的唯一情况，仅当我们只有一个元素需要排序时才这样做。