红黑树

17 Mar 2025 | 6 分钟阅读

红黑树是一类自平衡二叉搜索树。它由 Rudolf Bayer 于 1972 年创建，他称它们为“对称二叉 B 树”。

红黑树是一种二叉树，其中特定节点具有颜色作为额外的属性，红色或黑色。通过检查从根到叶子的任何简单路径上的节点颜色，红黑树确保没有这样的路径比任何其他路径长两倍以上，因此树通常是平衡的。

红黑树的特性

红黑树必须满足以下特性

根始终是黑色的。
nil 被认为是黑色的。这个因素是每个非 NIL 节点都有两个孩子。
黑色子节点规则：任何红色节点的子节点都是黑色的。
黑色高度规则：对于特定节点 v，存在一个整数 bh (v)，使得从 v 到 nil 的特定向下路径正确地具有 bh (v) 黑色真实（即非 nil）节点。将此部分称为 v 的黑色高度。我们确定 RB 树的黑色高度为其根的黑色高度。

如果根是红色的，但以上其他条件成立，则树 T 是一个几乎红黑树（ARB 树）。

RB 树上的操作

当在具有 n 个键的红黑树上运行时，搜索树操作 TREE-INSERT 和 TREE-DELETE 花费 O (log n) 时间。因为它们自定义了树，所以结论可能会违反红黑属性。为了恢复这些属性，我们必须更改树中某些节点的颜色，并更改指针结构。

1. 旋转

红黑树上的重组操作通常可以用旋转操作的细节更清楚地表达。

显然，顺序 (Ax By C) 由旋转操作保留。因此，如果我们从 BST 开始并且仅使用旋转进行重组，那么我们仍然会有 BST，即旋转不会破坏 BST 属性。

LEFT ROTATE (T, x)
 1. y ← right [x]
 1. y ← right [x]
 2. right [x] ← left [y]
 3. p [left[y]] ← x
 4. p[y] ← p[x]
 5. If p[x] = nil [T]
   then root [T] ← y
    else if x = left [p[x]] 									
      then left [p[x]] ← y
    else right [p[x]] ← y
 6. left [y] ← x.
 7. p [x] ← y.

示例：在键 {1, 2, 3... 15} 上绘制高度为 3 的完整二叉树。添加 NIL 叶子并以三种不同的方式对节点进行着色，使得生成的树的黑色高度为：2、3 和 4。

解决方案

黑色高度为 2 的树

黑色高度为 3 的树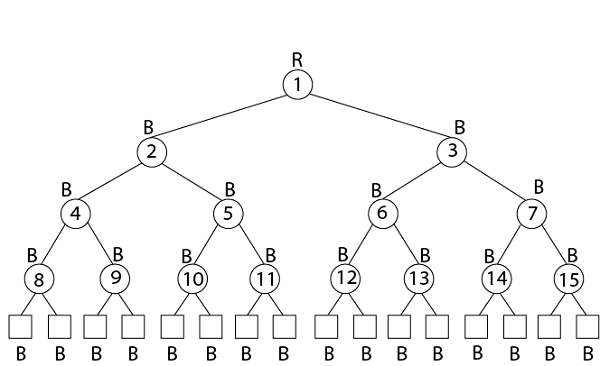

黑色高度为 4 的树

2. 插入

以在二叉搜索树中完成的方式插入新节点。
将节点涂成红色
如果红黑树出现不一致，请根据差异类型修复树。

差异可能源于父节点和子节点都具有红色。这种类型的差异由节点相对于祖父母的位置以及父节点的兄弟姐妹的颜色决定。

RB-INSERT (T, z)
 1. y ← nil [T]
 2. x ← root [T]
 3. while x ≠ NIL [T]
 4. do y ← x
 5. if key [z] < key [x]
 6. then x  ← left [x]
 7. else x ←  right [x]
 8. p [z] ← y
 9. if y = nil [T]
 10. then root [T] ← z
 11. else if key [z] < key [y]
 12. then left [y] ← z
 13. else right [y] ← z
 14. left [z] ← nil [T]
 15. right [z] ← nil [T]
 16. color [z] ← RED
 17. RB-INSERT-FIXUP (T, z)

插入新节点后，将这个新节点着色为黑色可能会违反黑色高度条件，而将这个新节点着色为红色可能会违反着色条件，即根是黑色的，并且红色节点没有红色子节点。我们知道黑色高度违规很难。所以我们把节点涂成红色。之后，如果存在任何颜色违规，那么我们必须通过 RB-INSERT-FIXUP 程序来纠正它们。

RB-INSERT-FIXUP (T, z)
 1. while color [p[z]] = RED
 2. do if p [z] = left [p[p[z]]]
 3. then y ← right [p[p[z]]]
 4. If color [y] = RED
 5. then color [p[z]] ← BLACK    //Case 1
 6. color [y] ← BLACK            //Case 1
 7. color [p[z]] ← RED           //Case 1
 8. z  ← p[p[z]]                 //Case 1
 9. else if z= right [p[z]]
 10. then z ← p [z]              //Case 2
 11. LEFT-ROTATE (T, z)          //Case 2
 12. color [p[z]] ← BLACK        //Case 3
 13. color [p [p[z]]] ← RED      //Case 3
 14. RIGHT-ROTATE  (T,p [p[z]])  //Case 3
 15. else (same as then clause)
      With "right" and "left" exchanged
 16. color [root[T]] ← BLACK

示例：显示在初始为空的红黑树中依次插入键 41、38、31、12、19、8 后产生的红黑树。

解决方案

插入 41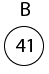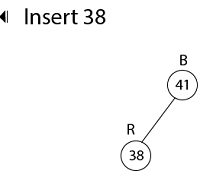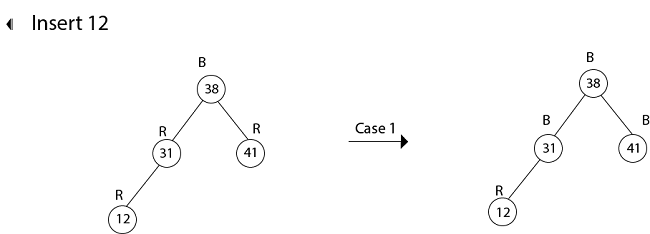

插入 19

因此，最终的树是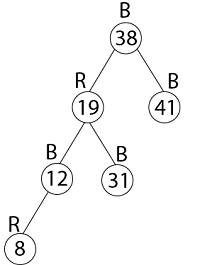

3. 删除

首先，搜索要删除的元素

如果要删除的元素位于只有左子节点的节点中，则将此节点与包含左子树中最大元素的节点交换。（此节点没有右子节点）。
如果要删除的元素位于只有右子节点的节点中，则将此节点与包含右子树中最小元素的节点交换（此节点没有左子节点）。
如果要删除的元素位于同时具有左子节点和右子节点的节点中，则以上述两种方式中的任何一种进行交换。交换时，仅交换键，而不交换颜色。
要删除的项目现在只有左子节点或只有右子节点。用其唯一的子节点替换此节点。这可能会违反红色约束或黑色约束。红色约束的违规可以很容易地修复。
如果删除的节点是黑色的，则黑色约束被违反。删除黑色节点 y 会导致包含 y 的任何路径都少一个黑色节点。
出现两种情况
- 替换节点是红色的，在这种情况下，我们只需将其着色为黑色，以弥补一个黑色节点的损失。
- 替换节点是黑色的。

策略 RB-DELETE 是 TREE-DELETE 过程的微小改变。在拼接出一个节点后，它会调用辅助程序 RB-DELETE-FIXUP，该程序会更改颜色并执行旋转以恢复红黑属性。

RB-DELETE (T, z)
 1. if left [z] = nil [T] or right [z] = nil [T]
 2. then y ← z
 3. else y ← TREE-SUCCESSOR (z)
 4. if left [y] ≠ nil [T]
 5. then x ← left [y]
 6. else x ← right [y]
 7. p [x] ←  p [y]
 8. if p[y] = nil [T]
 9. then root [T]  ← x
 10. else if y = left [p[y]]
 11. then left [p[y]] ← x
 12. else right [p[y]] ← x
 13. if y≠ z
 14. then key [z] ← key [y]
 15. copy y's satellite data into z
 16. if color [y] = BLACK
 17. then RB-delete-FIXUP (T, x)
 18. return y

RB-DELETE-FIXUP (T, x)
 1. while x ≠ root [T] and color [x] = BLACK
 2. do if x = left [p[x]]
 3. then w ← right [p[x]]
 4. if color [w] = RED
 5. then color [w] ← BLACK        //Case 1
 6. color [p[x]] ← RED            //Case 1
 7. LEFT-ROTATE (T, p [x])        //Case 1
 8. w ← right [p[x]]              //Case 1
 9. If color [left [w]] = BLACK and color [right[w]] = BLACK
 10. then color [w] ← RED         //Case 2
 11. x ← p[x]                     //Case 2
 12. else if color [right [w]] = BLACK
 13. then color [left[w]] ← BLACK //Case 3
 14. color [w] ← RED              //Case 3
 15. RIGHT-ROTATE (T, w)          //Case 3
 16. w ← right [p[x]]             //Case 3
 17. color [w] ← color [p[x]]     //Case 4
 18. color p[x] ← BLACK           //Case 4
 19. color [right [w]] ← BLACK    //Case 4
 20. LEFT-ROTATE (T, p [x])       //Case 4
 21. x ← root [T]                 //Case 4
 22. else (same as then clause with "right" and "left" exchanged)
 23. color [x] ← BLACK

示例：在前面的示例中，我们发现依次将键 41、38、31、12、19、8 插入到初始为空的树中而产生的红黑树。现在显示从成功删除顺序为 8、12、19、31、38、41 的键而产生的红黑树。

解决方案