最长递增子序列

在本主题中，我们将学习如何使用动态规划在数组中找到最长递增子序列。最长递增子序列是一个用于查找给定子序列中所有元素按递增顺序排序的最长子序列长度的问题。

让我们通过一个例子来理解。

考虑如下数组：

数组：0, 4, 12, 2, 10, 6, 9, 13, 3, 11, 7, 15

从上述数组可以构成以下子序列：

子序列1：8, 20, 40, 60, 70

子序列2：9, 21, 32, 49, 60, 70

同样，数组中可能存在更多子序列。子序列2的长度是所有子序列中最长的。子序列中的元素在原始数组中不必是连续的。现在，让我们看看如何直接确定子序列2是最长子序列。我们可以使用动态规划来找到最长子序列。

通过使用动态规划方法，我们将逐个位置地跟踪原始数组。我们将检查数组的每个索引，看它是否适合最长递增子序列。

首先，我们考虑两个变量 i 和 j，其中变量 'i' 指向数组的每个位置，对于每个 'i'，'j' 都从头开始。我们将考虑两个名为 'length' 和 'subsequence' 的数组，其中 length 数组将存储每个子序列的长度，subsequence 数组将存储子序列的元素。

动态规划的基线条件是，我们将每个数组单元格初始化为 1，如下所示。我们认为数组中的每个单个元素都是长度为 1 的最长递增子序列。

在 i=0 时

现在我们将找到长度大于 1 的子序列。如果我们从 i=0 开始；a[0] 包含值 1，这是到目前为止最长的递增子序列，并且已经找到了。所以，我们从索引 i=1 开始，对于 'i' 的每次增量，'j' 将再次从头开始。

在索引 i=1, j=0 时

由于 a[i]>a[j]，即 4>0，表示元素按递增顺序排列。索引 'i' 处的长度将等于索引 'j' 处的长度加 1，即 1+1 = 2。值 2 将添加到 length 数组的索引 1 处，如下所示。

i 的前一个索引将被添加到 subsequence 数组的 '1' 位置，如下所示。

由于 'j' 已经等于 'i'，所以 'i' 将被递增；'i' 的值变为 2，'j' 的值将再次从头开始，即 0。

在索引 i=2, j=0 时

现在我们将比较 a[i] 和 a[j]。由于 a[i] 大于 a[j]，即 12>0，表示元素按递增顺序排列。索引 'i' 处的长度将等于索引 'j' 处的长度加 1，即 1+1 = 2。值 2 将添加到 length 数组的索引 2 处，'j' 将被递增，如下所示。

在 i=2, j=1 时

由于 a[i] 大于 a[j]，即 12>4，表示元素按递增顺序排列。索引 'i' 处的长度将等于索引 'j' 处的长度加 1，即 2+1 = 3。我们将计算出的值与之前存储在索引 i 处的值进行比较。由于 3>2，因此在 length 数组的索引 'i' 处，2 被替换为值 3，如下所示。

i 的前一个索引将被添加到 subsequence 数组的索引 2 处，如下所示。

由于 'j' 已经等于 'i'，所以 'i' 将被递增；'i' 的值变为 3，'j' 的值将再次从头开始，即 0。

在索引 i=3, j=0 时

现在我们将比较 a[i] 和 a[j]。由于 a[i] 大于 a[j]，即 2>0，表示元素按递增顺序排列。索引 i=3 处的长度将等于索引 'j' 处的长度加 1，即 1+1 = 2。值 2 将添加到 length 数组的索引 3 处，'j' 将被递增，如下所示。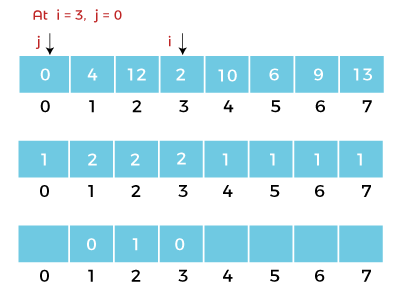

在 'j' 递增之前，'j' 指向索引 0。值 '0' 将添加到 subsequence 数组的索引 3 处，如下所示。由于 'j' 没有等于 'i'，因此值 0 没有固定在 subsequence 数组的索引 3 处。

在 j=1 时

现在，'j' 指向索引 1。a[j] 的值为 4，a[i] 的值为 2，表示 a[i]<a[j]。我们将递增 'j'，因为 4 不小于 2。一旦 'j' 被递增，'j' 的值将变为 2。

在 j=2 时

当 'j' 被递增时，我们将比较 a[i] 和 a[j]。由于 a[j] 大于 a[i]，即 12>2，表示不会进行更新。现在，'j' 将被递增，'j' 的值将等于 'i'，因此没有递增 'j' 的空间。

由于 'j' 已经等于 'i'，所以 'i' 将被递增；'i' 的值变为 4，'j' 的值将再次从头开始，即 0。

在索引 i=4, j=0 时

现在我们将比较 a[i] 和 a[j]。由于 a[i] 大于 a[j]，即 10>0，表示元素按递增顺序排列。索引 i=4 处的长度将等于索引 'j' 处的长度加 1，即 1+1 = 2。值 2 将添加到 length 数组的索引 4 处，'j' 将被递增，如下所示。

在 'j' 递增之前，'j' 指向索引 0。值 '0' 将添加到 subsequence 数组的索引 4 处，如下所示。由于 'j' 没有等于 'i'，因此值 0 没有固定在 subsequence 数组的索引 4 处。

在 j=1 时

现在，'j' 指向索引 1。a[j] 的值为 4，a[i] 的值为 10，表示 a[i]>a[j]。索引 i=4 处的长度将等于索引 'j' 处的长度加 1，即 2+1 = 3。值 3 将添加到 length 数组的索引 4 处，'j' 将被递增，如下所示。

在 'j' 递增之前，'j' 指向索引 1。值 '1' 将添加到 subsequence 数组的索引 4 处，如下所示。由于 'j' 没有等于 'i'，因此值 1 没有固定在 subsequence 数组的索引 4 处。

在 j=2 时

现在，'j' 指向索引 2。a[j] 的值为 12，a[i] 的值为 10，表示 a[i]<a[j]，即 12>10，表示不会进行更新。现在，'j' 将被递增，'j' 的值将变为 3。

在 j=3 时

由于 a[i]>a[j]，即 10>2，表示元素按递增顺序排列。索引 i=4 处的长度将等于索引 'j' 处的长度加 1，即 2+1 = 3。值 3 将添加到 length 数组的索引 4 处，'j' 将被递增，如下所示。

由于 'j' 已经等于 'i'，所以 'i' 将被递增；'i' 的值变为 5，'j' 的值将再次从头开始，即 0。

在索引 i= 5, j=0 时

由于 a[i]>a[j]，即 6>0，表示元素按递增顺序排列。索引 i=5 处的长度将等于索引 'j' 处的长度加 1，即 1+1 = 2。值 2 将添加到 length 数组的索引 5 处，'j' 将被递增，如下所示。

在 'j' 递增之前，'j' 指向索引 0。值 '0' 将添加到 subsequence 数组的索引 5 处，如下所示。由于 'j' 没有等于 'i'，因此值 0 没有固定在 subsequence 数组的索引 5 处。

在 j=1 时

现在，'j' 指向索引 1。由于 a[i] 大于 a[j]，即 4>6，这表示元素按递增顺序排列。索引 i=5 处的长度将等于索引 'j' 处的长度加 1，即 2+1 = 3。值 3 将添加到 length 数组的索引 5 处，'j' 将被递增，如下所示。

在 'j' 递增之前，'j' 指向索引 1。值 '1' 将添加到 subsequence 数组的索引 5 处，如下所示。由于 'j' 没有等于 'i'，因此值 1 没有固定在 subsequence 数组的索引 5 处。

在 j=2 时

现在，'j' 指向索引 2。由于 a[j] 大于 a[i]，即 12>6，表示不会进行更新。现在，'j' 将被递增，'j' 的值将变为 3。

在 j=3 时

现在，'j' 指向索引 3。由于 a[i] 大于 a[j]，即 6>2，表示元素按递增顺序排列。索引 i=5 处的长度将等于索引 'j' 处的长度加 1，即 2+1 = 3。值 3 将添加到 length 数组的索引 5 处，'j' 将被递增，如下所示。

在 'j' 递增之前，'j' 指向索引 2。值 '2' 将添加到 subsequence 数组的索引 5 处，如下所示。由于 'j' 没有等于 'i'，因此值 2 没有固定在 subsequence 数组的索引 5 处。

在 j=4 时

现在，'j' 指向索引 4。由于 a[j] 大于 a[i]，即 10>6，表示不会进行更新。现在 'j' 将被递增，'j' 的值将变为 5，如下所示。

由于 'j' 已经等于 'i'，因此没有递增的余地。'i' 的值将被递增，变为 6。'j' 将从头开始，即 j=0。

在索引 i=6, j=0 时

由于 a[i]>a[j]，即 9>0，表示元素按递增顺序排列。索引 i=6 处的长度将等于索引 j=0 处的长度加 1，即 1+1 =2。值 2 将添加到 length 数组的索引 i=6 处，'j' 将被递增，如下所示。

在 'j' 递增之前，'j' 指向索引 0。值 '0' 将添加到 subsequence 数组的索引 6 处，如下所示。由于 'j' 没有等于 'i'，因此值 0 没有固定在 subsequence 数组的索引 6 处。

在 j=1 时

现在 'j' 指向索引 1。由于 a[i] 大于 a[j]，即 9>4，表示元素按递增顺序排列。索引 i=6 处的长度将等于索引 j=1 处的长度加 1，即 2+1 = 3。我们将比较已存储在索引 6 处的值（即 2）与新计算出的值（即 3）。由于 3>2，因此在 length 数组的索引 6 处，2 被替换为 3，如下所示。

值 1 将添加到 subsequence 数组的索引 6 处，如下所示。'j' 的值将递增，值为 2。

在 j=2 时

现在，'j' 指向索引 2。由于 a[j] 大于 a[i]，即 12>9，表示不会进行更新。现在 'j' 将被递增，'j' 的值将变为 3，如下所示。

在 j=3 时

现在 'j' 指向索引 3。由于 a[i] 大于 a[j]，即 9>2，表示元素按递增顺序排列。索引 i=6 处的长度将等于索引 j=2 处的长度加 1，即 2+1 = 3。我们将比较已存储在索引 6 处的值（即 3）与新计算出的值（即 3）。由于两个值相同，因此无需修改。

值 3 将添加到 subsequence 数组的索引 6 处，如下所示，'j' 的值将被递增。

在 j=4 时

现在，'j' 指向索引 4。由于 a[j] 大于 a[i]，即 6>4，表示不会进行更新。现在 'j' 将被递增，'j' 的值将变为 5。

在 j=5 时

现在 j 指向索引 5。由于 a[i] 大于 a[j]，即 9>6，表示元素按递增顺序排列。索引 i=6 处的长度将等于索引 j=5 处的长度加 1，即 3+1=4。我们将比较已存储在索引 6 处的值（即 3）与新计算出的值（即 4）。由于 4>3，因此在 length 数组的索引 i=6 处，3 被替换为 4，如下所示。

值 5 将添加到 subsequence 数组的索引 6 处，如下所示，'j' 的值将递增。

在 j=6 时

在这种情况下，j 等于 'i'，因此不会进行更新。'i' 的值将被递增，变为 7。'j' 将从头开始，即 0。

在 i=7, j=0 时

由于 a[i] 大于 a[j]，即 13>0，表示元素按递增顺序排列。索引 7 处的长度将等于索引 j 处的长度加 1，即 1+1=2。我们将比较已存储在索引 7 处的值（即 1）与新计算出的值（即 2）。由于 2>1，因此在 length 数组的索引 i=7 处，1 被替换为 2，如下所示。

值 0 将添加到 subsequence 数组的索引 7 处，如下所示，'j' 的值将递增。

在 j=1 时

由于 a[i] 大于 a[j]，即 13>4，表示元素按递增顺序排列。索引 7 处的长度将等于索引 j 处的长度加 1，即 2+1=3。我们将比较已存储在索引 7 处的值（即 2）与新计算出的值（即 3）。由于 3>2，因此在 length 数组的索引 i=7 处，2 被替换为 3，如下所示。

值 1 将添加到 subsequence 数组的索引 7 处，如下所示，'j' 的值将递增。

在 j=2 时

由于 a[i] 大于 a[j]，即 13>12，表示元素按递增顺序排列。索引 7 处的长度将等于索引 j 处的长度加 1，即 2+1=3。我们将比较已存储在索引 7 处的值（即 3）与新计算出的值（即 4）。由于两个值相等，因此不会进行修改，'j' 的值将被递增。

值 2 将添加到 subsequence 数组的索引 7 处，如下所示，'j' 的值将递增。

在 j=3 时

由于 a[i] 大于 a[j]，即 13>2，表示元素按递增顺序排列。索引 7 处的长度将等于索引 j 处的长度加 1，即 2+1=3。我们将比较已存储在索引 7 处的值（即 3）与新计算出的值（即 3）。由于两个值相等，因此不会进行修改，'j' 的值将被递增。

值 3 将添加到 subsequence 数组的索引 7 处，如下所示，'j' 的值将递增。

在 j=4 时

由于 a[i] 大于 a[j]，即 13>10，表示元素按递增顺序排列。索引 7 处的长度将等于索引 j 处的长度加 1，即 3+1=4。我们将比较已存储在索引 7 处的值（即 4）与新计算出的值（即 4）。由于 4>3，因此在 length 数组的索引 i=7 处，3 被替换为 5，如下所示。

在 j=5 时

由于 a[i] 大于 a[j]，即 13>6，表示元素按递增顺序排列。索引 7 处的长度将等于索引 j 处的长度加 1，即 3+1=4。我们将比较已存储在索引 7 处的值（即 4）与新计算出的值（即 4）。由于两个值相等，因此不会进行修改，'j' 的值将被递增。

在 j=6 时

由于 a[i] 大于 a[j]，即 13>9，表示元素按递增顺序排列。索引 7 处的长度将等于索引 j 处的长度加 1，即 4+1=5。我们将比较已存储在索引 7 处的值（即 4）与新计算出的值（即 5）。由于 5>4，因此在 length 数组的索引 i=7 处，4 被替换为 5，如下所示。

值 6 将添加到 subsequence 数组的索引 7 处，如下所示，'j' 的值将递增。

这样，我们就找到了子序列的长度。在上面的 length 数组中，5 是最大长度。要找到长度为 5 的子序列，subsequence 数组中对应的单元格是索引 7。我们从索引 7 移动到索引 6，从索引 6 移动到索引 5，从索引 5 移动到索引 3，从索引 3 移动到索引 0。因此，索引是 0, 3, 5, 6, 7。这些索引处的元素是子序列。对应于这些索引的元素是 0, 2, 6, 9, 13。