Prim 的最小生成树算法

在计算机科学和数据结构领域，树在组织和高效管理数据方面起着至关重要的作用。树是分层结构，用于表示现实世界应用中的各种关系和层级。它们是算法和数据操作的基础，使其成为计算机科学领域的基石。在本文中，我们将深入探讨数据结构中的树的世界，探索其基本概念、类型和实际应用。

理解基础知识

在深入研究树的细节之前，让我们先建立一些基本概念

• 节点：节点是树的基本构建块。每个节点包含数据和零个或多个子节点。顶部的节点称为“根”，没有子节点的节点称为“叶子”。
• 边：边是树中节点之间的连接。它们表示节点之间的关系，指示哪些节点是父节点和子节点。
• 层级：树是分层结构，这意味着它们遵循特定的顺序和结构。节点以形成层级的方式组织，根节点位于顶部，下方有不同级别的子节点。

树的类型

树有多种形式，每种形式都旨在满足特定目的并解决不同问题。一些常见的树类型包括：

• 二叉树：在二叉树中，每个节点最多可以有两个子节点，通常称为左子节点和右子节点。二叉树广泛用于各种应用中，例如二叉搜索树和表达式树。
• 二叉搜索树 (BST)：二叉搜索树是一种二叉树，其中节点以允许高效搜索、插入和删除操作的方式组织。父节点左侧的节点值小于父节点，而右侧的节点值大于父节点。
• AVL 树：AVL 树是一种自平衡二叉搜索树。它通过确保任何节点的左子树和右子树的高度最多相差一，来维护平衡结构。这种平衡可确保高效的搜索操作。
• 红黑树：红黑树是另一种自平衡二叉搜索树。它使用一组规则来维护平衡结构，使其适用于广泛的应用。
• B 树：B 树是多路树，常用于数据库和文件系统中。它们通过维护具有可变数量子节点的平衡结构来提供高效的数据存储和检索。
• Trie：Trie（发音为“try”）是一种树状数据结构，用于存储和搜索动态字符串集，例如字典中的单词或路由器中的 IP 地址。

实际应用

现在我们已经探讨了树的基本概念和类型，让我们来看一些树在现实世界中的实际应用。

• 文件系统：文件系统，例如您计算机上的文件系统，通常使用树结构来组织文件和目录。每个目录都可以包含文件和子目录，形成分层结构。
• 数据库系统：许多数据库系统使用 B 树和其他树结构来高效地存储和检索数据。这些结构确保即使对于大型数据集也能快速访问数据。
• 网络路由：在计算机网络中，路由器使用基于树的算法来确定数据包从源到目标的最佳传输路径。
• 编译器设计：编译器使用抽象语法树 (AST) 来表示程序代码的结构。AST 对于解析和生成代码至关重要。
• 组织结构：树可以表示公司中的组织结构，每个节点代表一个员工或部门及其层级关系。
• 游戏开发：在视频游戏开发中，树用于管理游戏对象、它们的行为和交互。行为树是此用法的常见示例。

总之，树是计算机科学和数据结构中的一个基本概念。它们提供了一种有效的方式来组织和管理分层结构中的数据，使其在各种应用中都至关重要，从文件系统到数据库管理，甚至游戏开发。理解不同类型的树及其应用对于任何希望高效解决复杂问题的程序员或计算机科学家都至关重要。在后续的文章中，我们将更详细地探讨每种类型的树及其操作和算法。

理解贪婪算法：优化选择 步步为营

在计算机科学和优化领域，一种强大而直观的技术通常会脱颖而出，那就是贪心算法。贪心算法是多功能的解决问题策略，它们在每一步都做出决策，旨在最大化或最小化特定的目标函数。这些算法概念简单，但在广泛的应用中可能非常有效。在本文中，我们将深入探讨贪心算法的世界，探索其核心原理、优点和局限性。

什么是贪婪算法？

本质上，贪心算法通过做出一系列局部最优选择来达到全局最优解。它通过在每一步选择最佳选项来操作，而不考虑整体后果。这种短视的方法可以比作一个人在每个决策点持续选择眼前的最佳选项，希望达到最佳的整体结果。

贪婪算法的关键特征

1. 贪心选择性质

贪心算法的基本特征是其“贪心选择性质”。在每一步，算法都会选择在当前时刻看起来是最佳选择的选项，而不考虑大局。选择是根据特定标准做出的，该标准可能涉及最大化或最小化某个值。

2. 最优子结构

贪心算法依赖于“最优子结构”的概念，这意味着最优地解决一个较小的子问题有助于最优地解决较大的问题。换句话说，问题可以分解为较小的、可管理的子问题，这些子问题本身可以使用相同的贪心方法来解决。

Prim 算法简介

Prim 算法，以捷克数学家 Vojtěch Jarník 和计算机科学家 Robert C. Prim 的名字命名，是计算机科学和图论领域的基本算法。它属于贪心算法类别，主要用于在加权、连通图中查找最小生成树 (MST)。最小生成树在各种领域都有广泛的应用，包括网络设计、交通和电路布局优化。

理解最小生成树的概念

在深入研究 Prim 算法之前，理解最小生成树的概念至关重要。在图论中，连通无向图的生成树是一个包含原始图所有顶点的子图，并且形成一棵树。最小生成树是边权重之和最小的生成树。

最小生成树的意义出现在需要以最小总成本连接一组节点（代表地点、城市或其他实体）的情况下。例如，在设计通信网络时，您可能希望铺设电缆或光纤来连接多个位置，同时最大限度地减少总体电缆长度，这转化为成本节省。这正是 Prim 算法发挥作用的地方。

算法概述

Prim 算法从任意一个节点开始，通过添加连接树与图中其余部分的边来逐步构建最小生成树。以下是该算法工作原理的分步概述：

• 初始化：选择任意一个节点作为最小生成树的初始顶点。
• 候选边选择：识别连接当前最小生成树与尚未包含在树中的顶点的所有边。从这些边中，选择权重最小的一条。
• 添加到树：将选定的边添加到最小生成树中。
• 重复：通过将新添加的顶点视为最小生成树的一部分，并查找下一个候选边来继续此过程。
• 终止：重复步骤 2-4，直到所有顶点都包含在最小生成树中，从而得到一个跨越原始图所有节点的树。

算法说明

考虑以下图作为我们需要查找最小生成树 (MST) 的示例。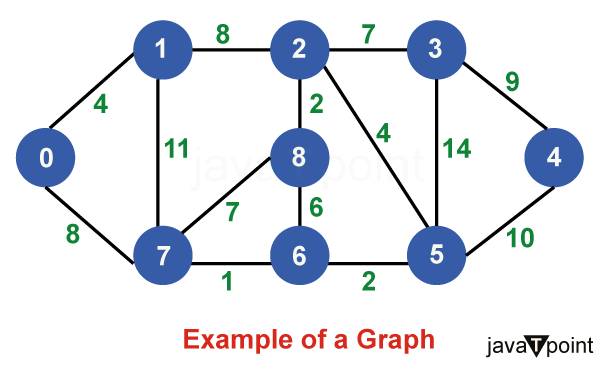

步骤 1：首先，我们选择一个任意顶点作为最小生成树的起始顶点。此处我们选择顶点 0 作为起始顶点。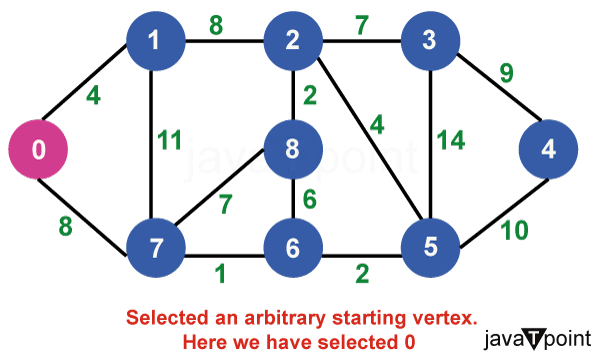

步骤 2：连接不完整 MST 和其他顶点的所有边是 {0, 1} 和 {0, 7}。在这两者之间，权重最小的边是 {0, 1}。因此，将边和顶点 1 包含在 MST 中。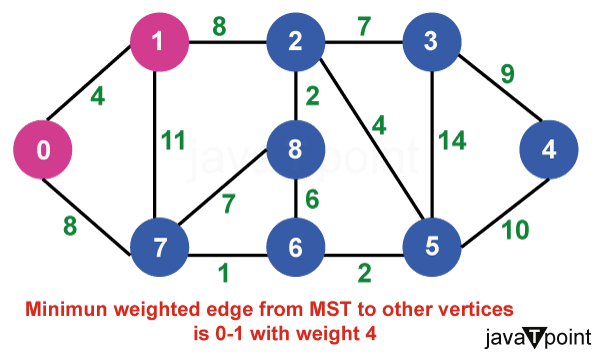

步骤 3：连接不完整 MST 与其他顶点的边是 {0, 7}、{1, 7} 和 {1, 2}。在这些边中，最小权重为 8，属于边 {0, 7} 和 {1, 2}。让我们在此包含边 {0, 7} 和顶点 7 到 MST 中。[我们也可以选择边 {1, 2} 和顶点 2 到 MST 中]。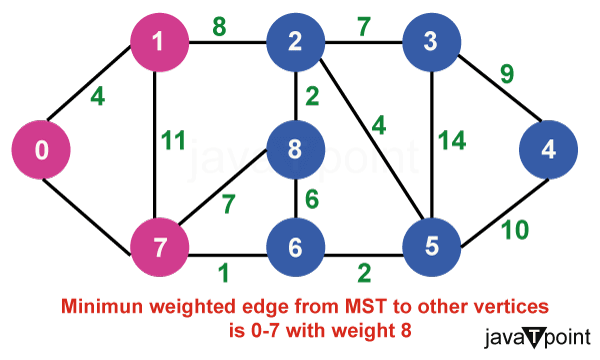

步骤 4：连接不完整 MST 与外部顶点的边是 {1, 2}、{7, 6} 和 {7, 8}。添加边 {7, 6} 和顶点 6 到 MST，因为它的权重最小（即 1）。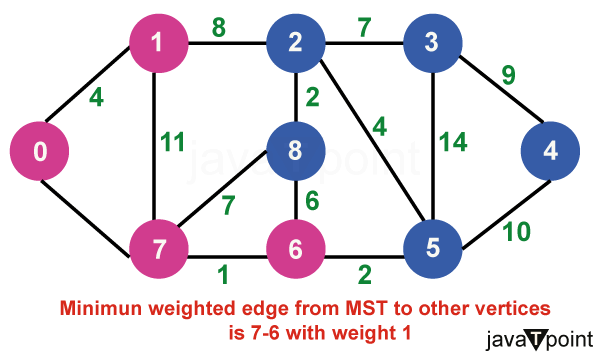

步骤 5：当前的连接边是 {7, 8}、{1, 2}、{6, 8} 和 {6, 5}。将边 {6, 5} 和顶点 5 添加到 MST，因为它们之间的边权重最小（即 2）。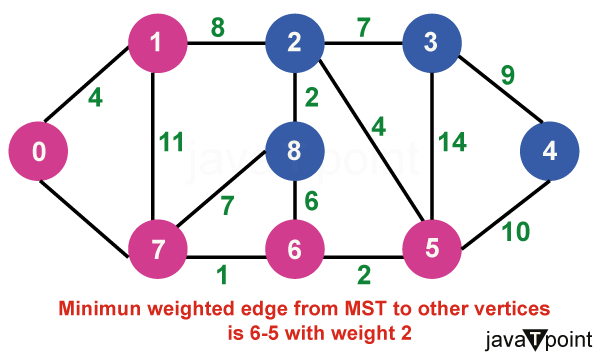

步骤 6：在当前连接边中，边 {5, 2} 的权重最小。因此，添加该边和顶点 2 到 MST 中。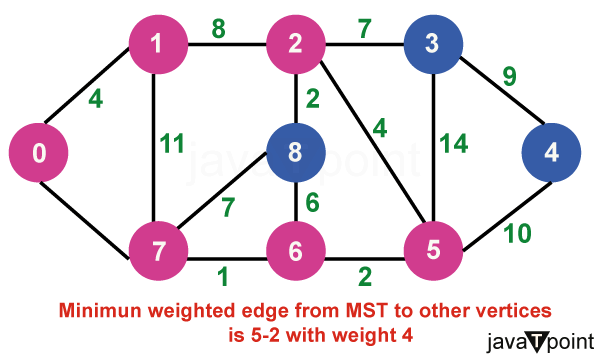

步骤 7：不完整 MST 与其他边之间的连接边是 {2, 8}、{2, 3}、{5, 3} 和 {5, 4}。权重最小的边是边 {2, 8}，其权重为 2。因此，添加该边和顶点 8 到 MST 中。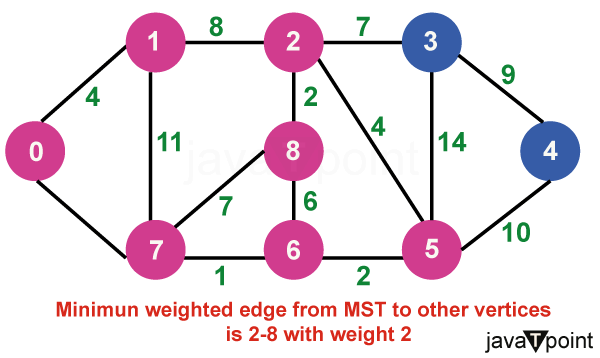

步骤 8：请注意，边 {7, 8} 和 {2, 3} 具有相同的最小权重。但 7 已经是 MST 的一部分。因此，我们将考虑边 {2, 3} 并将该边和顶点 3 添加到 MST 中。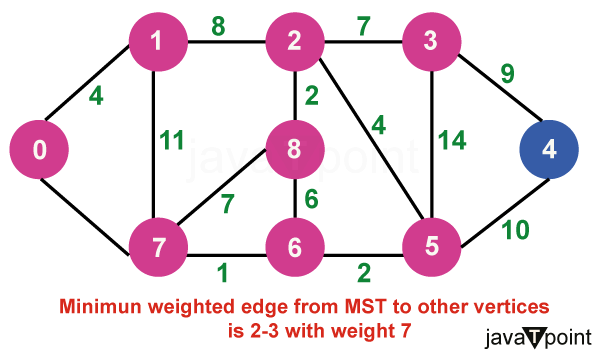

步骤 9：只剩下顶点 4 需要包含。从不完整 MST 到 4 的最小权重边是 {3, 4}。

MST 的最终结构如下，MST 的边权重为 (4 + 8 + 1 + 2 + 4 + 2 + 7 + 9) = 37。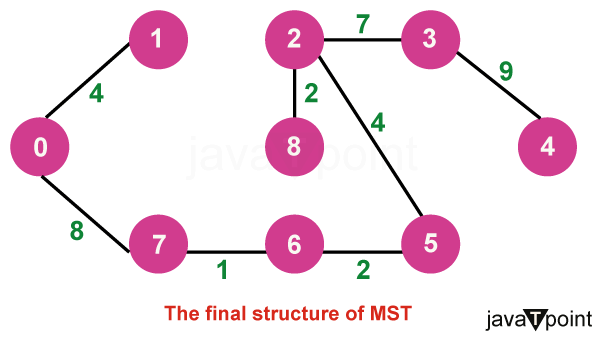

注意：如果我们选择第三步中的边 {1, 2}，那么 MST 将如下所示。

Prim 算法的关键特性

Prim 算法具有几个关键特性：

• 贪心策略：该算法通过在每一步选择最小权重的边来做出系列局部最优选择。这种贪心方法可确保最终的树是 MST。
• 连通性：该算法仅适用于连通图。如果输入图不连通，您需要分别将 Prim 算法应用于每个连通分量。
• 效率：Prim 算法以其效率而闻名，尤其是在使用优先级队列或堆等数据结构实现时。对于密集图，其时间复杂度为 O(V^2)，但使用优先级队列可以优化到 O(E + V log V)，其中 V 表示图中顶点的数量，E 表示边的数量。

Prim 算法的应用

Prim 算法在各种领域都有应用，包括：

• 网络设计：用于设计高效的通信和交通网络，同时最大限度地降低成本。
• 聚类分析：Prim 算法可用于数据聚类，其中它有助于识别连通分量或簇。
• 机器人技术：在机器人技术中，它可用于规划机器人穿越具有障碍物的连通环境的路径。
• 图像处理：Prim 算法在图像分割和特征提取中有应用，将图像视为加权图。
• 游戏开发：可用于高效生成迷宫或游戏地图。

结论：Prim 算法是用于在连通的加权图中查找最小生成树的一种通用且高效的算法。它的贪心性质、简单性和众多实际应用使其成为计算机科学和各个其他领域的宝贵工具。通过系统地选择最小权重的边，Prim 算法为以最小总成本连接一组节点的问题提供了最佳解决方案，使其成为图论和优化领域的基本算法。

Prim 算法如何工作？

Prim 算法的工作原理可以通过以下步骤描述：

步骤 1：确定一个任意顶点作为 MST 的起始顶点。

步骤 2：直到存在尚未包含在 MST 中的顶点（称为外部顶点）为止，执行步骤 3 到 5。

步骤 3：查找连接任何树顶点与外部顶点的边。

步骤 4：查找这些边中的最小值。

步骤 5：如果所选边不形成任何环，则将其添加到 MST 中。

步骤 6：返回 MST 并退出。

以下是 Prim 最小生成树算法的程序：

输出

Edge     Weight
0 - 1     2 
1 - 2     3 
0 - 3     6 
1 - 4     5
.............................
Process executed in 1.11 seconds
Press any key to continue

说明

1. #include <bits/stdc++.h>：这行包含一个标准 C++ 库头文件，其中包含各种其他头文件，方便进行竞争性编程和快速开发。但是，不推荐在生产代码中使用。
2. using namespace std;：这行允许您在不显式指定的情况下使用 std 命名空间中的名称。在 C++ 中，这是一种常见做法，但在较大的程序中可能导致命名冲突。
3. #define V 5：这行定义了一个常量 V，值为 5，表示图中顶点的数量。
4. int minKey(int key[], bool mstSet[])：这是 minKey 函数的定义。它接受两个数组作为参数：key（每个顶点的键数组）和 mstSet（一个布尔数组，用于跟踪顶点是否包含在 MST 中）。此函数在尚未包含在 MST 中的顶点集中查找具有最小键值的顶点，并返回其索引。
5. void printMST(int parent[], int graph[V][V])：此函数负责打印构建的 MST。它接受两个参数：parent（一个存储 MST 中每个顶点的父项的数组）和 graph（表示原始图的邻接矩阵）。它打印 MST 中的边及其权重。
6. void primMST(int graph[V][V])：这是 Prim MST 算法的主函数。它以邻接矩阵 graph 作为输入并构建 MST。
7. int parent[V];：一个用于存储 MST 中每个顶点的父项的数组。
8. int key[V];：一个用于存储每个顶点键值（权重）的数组。初始化为无穷大 (INT_MAX)。
9. bool mstSet[V];：一个布尔数组，用于跟踪顶点是否包含在 MST 中。对所有顶点都初始化为 false。
10. 循环将所有键初始化为无穷大，并将所有 mstSet 设置为 false。
11. 将第一个顶点（0）的键设置为 0，使其成为 MST 的起点。
12. 将第一个顶点的父项初始化为 -1，表示它没有父项（它是 MST 的根）。
13. 循环用于构建 MST。它运行 V-1 次，因为 MST 有 V-1 条边。
14. 在循环内部，它调用 minKey 来查找尚未包含在 MST 中的顶点中具有最小键值的顶点 u。
15. 它将顶点 u 添加到 MST，将 mstSet[u] 设置为 true。
16. 如果它们尚未包含在 MST 中，并且到它们的边的权重小于它们当前的键值，则更新 u 的邻接顶点的键值和父索引。
17. 构建 MST 后，它调用 printMST 来打印 MST 中的边及其权重。

以下是 Prim 最小生成树算法的 C 语言程序：

输出

Edge     Weight
0 - 1     2 
1 - 2     3 
0 - 3     6 
1 - 4     5
.............................
Process executed in 1.11 seconds
Press any key to continue

说明

1. #include <limits.h>：这行包含标准 C 库头文件 limits.h，其中包含与数据类型相关的各种常量，包括不同类型的最大值和最小值。
2. #include <stdbool.h>：这行包含标准 C 库头文件 stdbool.h，其中定义了 bool 类型及其值 true 和 false。
3. #include <stdio.h>：这行包含标准 C 库头文件 stdio.h，它对于输入和输出操作是必需的。
4. #define V 5：这行定义了一个宏 V，值为 5，表示图中顶点的数量。
5. int minKey(int key[], bool mstSet[])：这行声明了一个 minKey 函数，它接受两个数组 key 和 mstSet 作为参数。此函数用于在尚未包含在 MST 中的顶点集中查找具有最小键值的顶点。
6. int min = INT_MAX, min_index;：这行声明了两个整数变量 min 和 min_index，并使用 limits.h 库中的 INT_MAX 将 min 初始化为最大可能的整数值。
7. for (int v = 0; v < V; v++)：这行开始一个循环，该循环遍历图的所有顶点。
8. if (mstSet[v] == false && key[v] < min)：这行检查顶点 v 是否尚未包含在 MST 中 (mstSet[v] == false)，以及顶点 v 的键值是否小于当前最小值 (key[v] < min)。
9. min = key[v], min_index = v;：如果上述条件为真，则将最小值 min 更新为顶点 v 的键值，并将 min_index 设置为 v。
10. return min_index;：函数返回具有最小键值的顶点的索引。
11. int printMST(int parent[], int graph[V][V])：这行声明了一个 printMST 函数，它接受一个 parent 数组和一个 graph 二维数组作为参数。此函数用于打印构建的 MST。
12. printf("Edge \tWeight\n");：这行打印 MST 边及其权重的列标题。
13. for (int i = 1; i < V; i++)：这行开始一个循环，该循环从 1 迭代到 V-1，表示 MST 中的边。
14. printf("%d - %d \t%d \n", parent[i], i, graph[i][parent[i]]);：这行打印 MST 中第 i 条边的边、权重和换行符。
15. void primMST(int graph[V][V])：这行声明了 primMST 函数，它接受一个 graph 二维数组作为参数。此函数负责查找和打印 MST。
16. int parent[V];：这行声明了一个整数数组 parent，用于存储 MST 中每个顶点的父项。
17. int key[V];：这行声明了一个整数数组 key，用于存储每个顶点的键（最小边权重）。
18. bool mstSet[V];：这行声明了一个布尔数组 mstSet，用于跟踪每个顶点是否包含在 MST 中。
19. for (int i = 0; i < V; i++)：这行将 key 数组初始化为最大值，并将所有顶点设置为尚未包含在 MST 中。
20. key[0] = 0;：第一个顶点（起始顶点）的键值设置为 0。
21. parent[0] = -1;：第一个顶点的父项设置为 -1，表示它是 MST 的根。
22. for (int count = 0; count < V - 1; count++)：这行开始一个循环，该循环迭代 V-1 次，因为 MST 有 V-1 条边。
23. int u = minKey(key, mstSet);：它调用 minKey 函数来查找尚未包含在 MST 中的顶点中具有最小键值的顶点。
24. mstSet[u] = true;：顶点 u 被标记为包含在 MST 中。
25. for (int v = 0; v < V; v++)：此循环遍历图中的所有顶点。
26. if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])：这行检查顶点 u 和 v 之间是否存在边（即 graph[u][v] 非零），顶点 v 是否尚未包含在 MST 中 (mstSet[v] == false)，以及 u 和 v 之间边的权重是否小于顶点 v 的当前键值。
27. parent[v] = u, key[v] = graph[u][v];：如果上述条件为真，则将顶点 v 的父项更新为 u，并将顶点 v 的键值更新为 u 和 v 之间的边的权重。
28. printMST(parent, graph);：最后，它调用 printMST 函数来打印构建的 MST。
29. int main()：这行声明了 main 函数，它是程序的入口点。
30. int graph[V][V] = { { 0, 2, 0, 6, 0 }, ... };：这行使用输入图的邻接矩阵表示来初始化图矩阵。
31. primMST(graph);：它调用 primMST 函数来查找给定图的最小生成树并打印它。
32. return 0;：main 函数返回 0，表示程序成功执行。
33. 此 C 程序使用 Prim 算法计算图的最小生成树，并打印 MST 中的边及其权重。

上述代码的时间和空间复杂度分析

时间复杂度

• 初始化：代码初始化了 key、parent 和 mstSet 等各种数组，这需要 O(V) 的时间，其中 V 是图中顶点的数量。
• 主循环：primMST 函数中的主循环迭代 V 次，其中 V 是图中顶点的数量。在每次迭代中，它执行以下步骤：
• minKey 函数调用：它调用 minKey 函数来查找具有最小键值的顶点，这需要 O(V) 的时间。
• 更新键值和父项：它更新邻接顶点的键值和父索引。在最坏的情况下，这涉及为每个顶点扫描所有边，这导致循环内的 O(V^2) 操作。
• 打印 MST：构建 MST 后，调用 printMST 函数，该函数遍历 V 个顶点一次以打印 MST 边。这需要 O(V) 的时间。

总而言之，此代码中 Prim 算法的时间复杂度主要由主循环决定，由于邻接矩阵表示，最坏情况下为 O(V^2)。但是，使用更有效的数据结构（如邻接表），时间复杂度可以降低到 O(V^2) 甚至 O(V*log(V))，具体取决于实现。

空间复杂度

• 邻接矩阵：空间复杂度主要由邻接矩阵 graph 决定，它消耗 O(V^2) 的空间，因为它存储了 V 个顶点之间所有可能边的权重。
• 数组：代码使用大小为 V 的 key、parent 和 mstSet 数组。因此，这些数组的空间复杂度为 O(V)。

其他变量：有几个整数变量用于循环和临时存储，与数组相比，它们的空间复杂度可以忽略不计。

优化版本

输出

4
......
Process executed in 0.11 seconds
Press any key to continue

说明

1. #include<bits/stdc++.h>：这行包含一个预处理器指令，该指令导入一组常用的标准 C++ 库，包括数据结构（如 vector 和 priority_queue）所需的库。
2. using namespace std;：这行表明代码正在使用标准 C++ 命名空间，这允许您使用标准 C++ 类和函数，而无需在它们前面加上“std::”。
3. typedef pair<int,int> pii;：这行定义了一个别名 pii，用于数据类型 pair<int, int>。这通常用于使代码更具可读性和简洁性。
4. int spanningTree(int V, int E, int edges[][3])：这行声明了一个名为 spanningTree 的函数，它接受三个参数：V（顶点数）、E（边数）以及包含边及其权重信息的二维数组 edges。
5. {：表示 spanningTree 函数开始的花括号。
6. vector<vector<int>> adj[V];：这行声明了一个名为 adj 的二维向量，用于表示具有 V 个顶点的图的邻接列表。它将每个顶点的邻接列表初始化为空向量。
7. for (int i = 0; i < E; i++) {：开始一个循环，该循环遍历 edges 数组中的每条边。
8. int u = edges[i][0];：提取当前边的源顶点。
9. int v = edges[i][1];：提取当前边的目标顶点。
10. int wt = edges[i][2];：提取当前边的权重。
11. adj[u].push_back({v, wt});：将目标顶点及其权重添加到顶点 u 的邻接列表中。
12. adj[v].push_back({u, wt});：由于这是一个无向图，它还将顶点 u 和相同的权重添加到顶点 v 的邻接列表中。
13. }：处理边的循环结束。
14. priority_queue<pii, vector<pii>, greater<pii>> pq;：这行声明了一个名为 pq 的优先级队列，用于按权重升序存储边（表示为顶点和权重的对）。greater<pii> 比较器确保较小的权重位于队列的前面。
15. vector<bool> visited(V, false);：初始化一个名为 visited 的布尔向量，用于跟踪每个顶点是否已被访问。
16. int res = 0;：初始化一个变量 res，用于存储结果（边权重之和）。
17. pq.push({0, 0});：将第一个顶点（顶点 0）放入优先级队列，权重为 0，以启动 Prim 算法。
18. while (!pq.empty()) {：循环开始，直到优先级队列为空。
19. auto p = pq.top();：从优先级队列中检索顶部元素（权重最小的边）。
20. pq.pop();：从优先级队列中删除顶部元素。
21. int wt = p.first;：提取边的权重。
22. int u = p.second;：提取与边相连的顶点。
23. if (visited[u] == true) { continue; }：检查顶点 u 是否已被访问。如果是，则跳过处理此边。
24. res += wt;：将边权重添加到结果中。

时间和空间复杂度分析

时间复杂度分析

• 邻接表创建：代码首先从给定的边列表中创建邻接表。这包括一次遍历所有边并将它们添加到各自的邻接列表中。此步骤的时间复杂度为 O(E)，其中 E 是边的数量。
• 优先级队列操作：在 while 循环中，代码会重复从优先级队列中提取最小权重的边。在最坏的情况下，优先级队列最多可以包含 E 条边。从优先级队列中提取最小元素需要 O(log E) 时间。由于此操作对所有边执行，因此优先级队列操作的总时间为 O(E * log E)。
• 遍历邻接列表：在循环内部，代码会遍历当前顶点的邻接列表。在最坏的情况下，当图密集时，此循环可能会运行 E 次（每条边一次）。每次迭代都涉及常数时间操作，例如检查顶点是否已被访问以及将元素推入优先级队列。因此，这部分也贡献了 O(E) 的时间。
• 总而言之，此代码中时间复杂度的主要影响因素是优先级队列操作，其复杂度为 O(E * log E)。因此，此代码的整体时间复杂度为 O(E * log E)。

空间复杂度分析

• 邻接表：代码创建了图的邻接表表示，其空间复杂度为 O(V + E)，其中 V 是顶点数，E 是边数。
• 优先级队列：优先级队列任何时候最多存储 E 个元素，因此其空间复杂度为 O(E)。
• 访问数组和其他变量：代码使用大小为 V 的访问数组，其空间复杂度为 O(V)。此外，还有其他一些消耗常数空间的变量。
• 总而言之，此代码的空间复杂度为 O(V + E)。

总之，提供的代码使用 Prim 算法高效地查找图的 MST，其时间复杂度为 O(E * log E)，空间复杂度为 O(V + E)。这些复杂度使其适用于相对较大的图，特别是当边数与顶点数相比不是过大时。

优点

• Prim 算法保证在连通的加权图中找到 MST。
• 使用二叉堆或 Fibonacci 堆，其时间复杂度为 O(E log V)，其中 E 是边数，V 是顶点数。
• 与其他一些 MST 算法相比，它是一种相对容易理解和实现的算法。

缺点

• 与 Kruskal 算法一样，Prim 算法在边数很多的情况下，对于密集图可能会变慢，因为它需要至少迭代所有边一次。
• Prim 算法依赖于优先级队列，这可能会占用额外的内存，并在非常大的图上减慢算法的速度。
• 起始节点的选择会影响 MST 的输出，这在某些应用中可能是不受欢迎的。