集合覆盖

集合覆盖问题：它是什么？

在组合优化中，集合覆盖问题是一个重要的NP难问题。集合覆盖问题旨在确定包含（覆盖）给定项目集合的最少集合数量。

集合覆盖问题是复杂性理论、运筹学、计算机科学和组合学中的一个著名问题。Karp在1972年证明的21个NP完全问题之一。

给定一个元素集合1, 2,..., n（称为全集）和一个集合S，集合覆盖问题是找到S的一个最小子集，其并集等于全集。例如，考虑全集U = 1, 2, 3, 4, 5和集合S = {1, 2}, {1, 3}, {2, 4}, {3, 4}。S的并集无疑是U。然而，以下更少的集合可能包含所有元素：{1, 2, 3} 和 {3, 4}。或者{1, 2}和{3, 4}。这是因为集合{1, 2, 3}和{3, 4}的并集为{1, 2, 3, 4}，而集合{1, 2}和{3, 4}的并集为{1, 2, 3, 4}。

形式上，给定一个全集和一个子集族，覆盖是指一个子族，其并集等于全集。集合覆盖的判定问题询问是否存在一个大小为k或更小的集合覆盖，其输入是一对和整数。集合覆盖的优化问题旨在找到一个使用最少集合的集合覆盖。输入是一对。

集合覆盖的判定形式是NP完全的，而优化/搜索形式是NP难的。根据[1]，这是一个“其研究已推动了整个逼近算法领域基本技术发展”的挑战。[2] 当每个集合都给定成本时，就会创建一个加权集合。

为什么集合覆盖问题是NP完全的？

给定一个基集X、一个整数k以及X的子集Si的集合，确定是否存在一个子集族，其并集为X且大小不超过k。证明：问题的一个实例是给该问题的输入。

给定一个基集X、一个整数k以及X的子集Si的集合，确定是否存在一个子集族，其并集为X且大小不超过k。

证明

问题的输入是该问题的一个实例。集合覆盖问题的例子包括基集X、整数k以及由X生成的子集Si的集合。由于NP完全问题根据定义既是NP又是NP难问题，所以声称一个问题是NP完全的包含两个部分：

1. 该问题本身是NP完全的。
2. 所有其他NP类问题都可以以多项式时间归约到它。（B可以通过多项式时间归约到C）。

如果仅满足第二个条件，则该问题称为NP难。然而，只有在某些情况下，才能将每个NP问题转化为另一个NP问题来证明其NP完全性。因此，如果我们想证明一个问题是NP完全的，我们必须证明它属于NP，并且任何NP完全问题都可以归约到它。以下命题可用于证明集合覆盖问题是NP完全的：

1. 集合覆盖属于NP：如果任何问题属于NP，那么给定一个“证书”（问题的解决方案）和一个问题实例（子集集合C，大小为k），我们可以在多项式时间内识别证书（无论解决方案是否正确）。如果你提供一个大小为k的子集集合C，我们可以遍历子集集合中的每个元素，并标记X中的项已覆盖。最终X中不应有任何未揭示的项。X中的子集数量需要多项式时间。因此，集合覆盖属于NP。
2. 集合覆盖是NP难的：为了证明集合覆盖是NP难的，我们将把顶点覆盖（一个著名的NP难问题）归约到集合覆盖问题。图G = (V, E)和数字k是顶点覆盖问题的输入。令G中的边集为基集，即

• X = E。
• 包含在子集Su中的是每个顶点v∈V的关联边。

现在，以下两个命题是正确的：

• 假设k表示Su1, Su2。Suk覆盖的基集X中的每条边都至少与u1...uk中的一个顶点相邻，从而形成大小为k的顶点覆盖。
• 如果顶点u1和uk构成一个顶点覆盖，那么Su1将覆盖所有与u1相交的边。因此，集合Su1, Su2...Suk构成覆盖X的集合。
• 集合覆盖既属于NP又属于NP难。因此，集合覆盖是NP完全的。

图上的集合覆盖是什么？

独立集合问题与集合覆盖问题相同。这是通过指出集合覆盖问题的一个实例可以被理解为一个任意二分图，左侧的顶点表示全集，右侧的顶点表示集合，边表示集合中元素的包含关系来证明的。

独立集

一组顶点。换句话说，一组非相邻顶点如果其任意两个顶点都不相邻，则称为独立集。

它通常被称为稳定集。

• G的独立数，即非相邻顶点的最大数量，由公式0(G) = max |I|: I是G中的独立集定义。
• 一个最大独立集是一个独立集I，其中|I| = 0(G)。

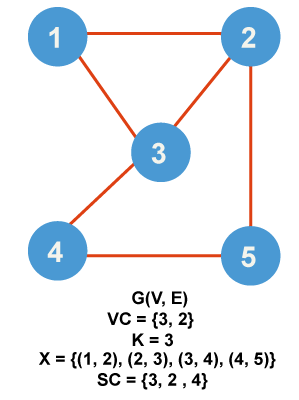
上面显示的图G的独立集是I1 = {1}, I2 = {2}, I3 = {3}, I4 = {4}。

I5 = {1, 3} 和 I6 = {2, 4}

因此，独立数0(G) = 2，这是非相邻顶点的最大数量。

顶点覆盖

• 如果图G的每条边都被集合K中的一个顶点覆盖，那么集合K就被称为G的顶点覆盖。
• G的顶点覆盖数，即可以完全覆盖所有边的最小顶点数，由参数0(G) = min |K|: K是G的顶点覆盖定义。
• 最小顶点覆盖是任何顶点覆盖K，其中|K| = 0(G)。

上面显示的图G的顶点覆盖如下：V1 = {1, 3}; V2 = {2, 4}; V3 = {1, 2, 3}; V4 = {1, 2, 3, 4}; 等等。

因此，完全覆盖所有边所需的最小顶点数为2，即顶点覆盖数0(G)。

如果I是G的顶点覆盖，那么V(G) - I是G中的一个独立集。

• 对于任何图G，n是顶点数，并且0(G) + 0(G) = n。
• 边覆盖：如果图G的每个顶点都与边集F中的一条边相连，那么该边集F就被称为图G的边覆盖。
• G的边覆盖数，即可以覆盖所有顶点的最小边数，由参数1(G) = min |F|: F是G的边覆盖定义。它等于孤立顶点的数量（如果存在）加上可以覆盖所有顶点的最小边数。
• 最小边覆盖是任何边覆盖F，其中|F| = 1(G)。

上面显示的图G的边覆盖如下：E1 = {"a", "b", "c", "d"}, E2 = {"a", "d"}, E3 = {"b", "c"}。

边覆盖数1(G) = 2，即可以覆盖所有顶点的最小边数为2。

任何图G的顶点数n等于1(G) + 1(G)。

比较

• G中不相邻的边集称为匹配集；它是一个边独立集，其中没有两条边是连续的。
• G的匹配数由参数1(G) = max |M|定义，指的是非相邻边的最大数量。
• 最大匹配是任何匹配M，其中|M| = 1(G)。

上面显示的图G的匹配值是M1 = {"a"}, M2 = {"b"}, M3 = {"c"}, M4 = {"d"}, M5 = {"a", "d"}, M6 = {"b", "c"}。

因此，非相邻边的最大数量，即匹配数1(G)，为2。

完美匹配：如果一个匹配包含图G的所有顶点，则称其为完全匹配。有时也称为完美匹配。

霍尔婚姻定理：二分图G =(V, E)具有二分（V1, V2），当且仅当对于V1的所有子集A，都有|N (A)| ≥ |A|（这是完全匹配的充要条件）。

顶点覆盖问题是NP难的吗？

顶点覆盖问题是Karp的21个NP完全问题之一，它是一个NP完全问题。

集合覆盖问题是NP完全的吗？

集合覆盖具有NP完全性定理。证明：首先，我们声称集合覆盖属于NP，因为给定一个集合族C，一个验证者可以快速确定C是否包含所有地面集U中的元素，以及C中提到的所有集合的并集是否包含这些元素。

最小子集覆盖问题：它是什么？

假设X中的每个元素至少属于一个集合；因此j S j = X。称集合I ⊆ {1, 2,..., m}，使得j∈I Sj = X为X的一个集合覆盖。大小最小的集合覆盖I是MIN-SET-COVER问题的答案。称为最小集覆盖的是覆盖X的最小集合Si1, Si2,..., Sik。

边覆盖是NP完全的，对吗？

测量整个边覆盖。t-总边覆盖问题目前正在考虑中。因此，该问题转化为多项式可解的边覆盖问题，该问题长期以来一直存在[8]。对于每个固定的t ≥ k，该问题是NP完全的[9，定理3]。

如何确定顶点覆盖？

顶点覆盖

1. 近似顶点覆盖 (G = (V, E))
2. C = 空集；3.
3. E' = E;
4. 当E'不为空时执行。
5. {
6. 假设E'中的任意边为(u, v): (*)
7. 将C添加到u和v；

如果图中的一条边子集D被认为是边支配集，则图中的每条边要么在D中，要么与D中的边共享一个端点。找到最小基数边支配集是最小边支配集问题的目标。已知该问题的判定形式是NP完全的，但我想知道是否有非常简短的证明。

Gavril和Yannakakis最初处理该问题的工作中，是我在文献中能找到的唯一证据。然而，如前所述，证明利用了顶点覆盖对于平面三次图是NP完全的性质。d-边着色对于d次二分图是可能的。如果能有一个使用在修读过算法课程的本科生通常理解的知识来证明会更好。

最大覆盖选址问题：它是什么？

最大覆盖选址问题旨在确定在给定服务距离或时间的情况下，在有限数量的设施下可以服务的最大人口数量。

由于其解决方案在现实世界中满足全部需求是不可能的，因此它们具有实际应用，因此最大覆盖选址问题受到了大量的研究关注。例如，这些解决方案可用于部署消防站、医院和商业服务，或提供人道主义援助。然而，覆盖范围通常取决于客户到设施的便利性、设施在特定区域（或半径）内服务客户的能力，或提供服务的速度。在本研究中，我们假设设施具有小的服务区域，并且需求中心点的人口足够移动，以便在合理距离内寻求他们的需求。我们构建了一个最大覆盖选址问题，该问题基于后一种假设优化可达性度量。行程成本函数、地理离散化、在移动半径内可获得机会的需求中心点数量、机会的数量和位置以及需求中心的覆盖范围都用于加权可达性指标。我们使用混合整数线性规划来定义我们的优化问题；在随机生成的实例上进行的测试表明，商业求解器可以快速地为大型实例生成近乎最优的结果。此外，我们使用墨西哥一个社会经济弱势地区的信息，对各种服务和移动半径进行了敏感性分析。最后，我们使用线性最差方法计算指示对各种可达性指标的主观偏好的权重参数。

一个多世纪以来，设施选址一直是研究的关键主题。由于其在天然气站、学校、工厂、垃圾填埋场、警察局等的部署中的应用，它在供应链的成功中起着至关重要的作用。覆盖选址问题是一个著名的研究问题，自选址科学早期以来就得到了研究。在覆盖选址挑战中，寻求解决方案以在考虑一个或多个目标和特定数量的设施的情况下服务一部分客户。

位置集合覆盖问题（LSCP）和最大覆盖位置问题（MCLP）是覆盖位置问题的两个常见分类。在传统的MCLP中，目标是定位网络上的各种设施以最大化被覆盖的人口。如果一个设施的建造距离需求节点比阈值近，则覆盖该需求节点。覆盖半径，一个用来描述这个预定阈值的术语，直接影响问题的解决方式。

Church和ReVelle最初在网络上建立了MCLP，此后，对原始问题进行了许多补充。当资金或资源不足以满足所有人的需求时，通常会考虑MCLP。决策者设定了一个固定的预算或资源来尽可能全面地满足需求。它展示了一个使用20个设施的模型答案。此图显示了设施为粗节点，它们各自的覆盖区域显示为圆。此外，需要覆盖的需求中心点为小点。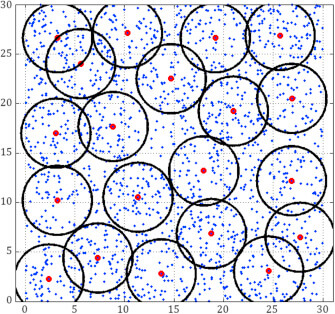

MCLP的不同变体已通过多种方法解决。这些包括下一节涵盖的精确、启发式和元启发式方法。使用精确方法，解决许多MCLP实例很困难。因此，为了解决更大规模的MCLP，使用了启发式和元启发式方法。ReVelle等人最近报告了一种解决MCLP的启发式集中方法，并实现了900个节点的解决方案。在本研究中，我们解决了包含多达2500个节点的问题，并展示了建议的GA在测试用例上的表现。我们的研究表明，GA可以高效且错误很少地处理复杂问题。

在此模型研究之前，有一些假设。当至少有一个设施在节点一定半径范围内时，假设它被覆盖。此外，每个节点都可以托管一个设施。换句话说，节点集和潜在设施集之间没有区别。此外，假设每个节点都有一个必须满足的特定需求。

此外，人们应该靠近这些便利设施。这意味着本文的范围不包括垃圾填埋场等地方。此外，还考虑了MCLP，它是外源的。

最大覆盖问题是什么？

最大覆盖问题是该问题的著名推广，由Junade Ali和Vladimir Dyo首次书面讨论。任务是找到最大覆盖。当所有权重都最大化时（最大化覆盖元素的加权和），基本版本是一个特例。

最大覆盖问题（MCP）是计算机科学和组合优化中一个著名的优化问题。

以下是其形式化定义：

• 全集是一个有限集U，包含元素e1, e2,..., en。
• 一个集合S包含m个U的子集，其中每个Si ⊆ U。S = S1, S2,..., Sm。
• 一个整数k，范围为1到m。

目标是找到一个子集C ⊆ S，其中恰好有k个子集，并且这些子集覆盖的元素数量最多。

鉴于它可以很容易地归约到集合覆盖问题（已知为NP完全），最大覆盖问题实际上是NP难的。MCP要求在给定数量的集合下覆盖的最多元素数量，而集合覆盖的优化版本要求使用最少的集合来覆盖全集中的每个元素。

贪婪方法可以为最大覆盖问题获得最佳解决方案的(1 - 1/e)倍的因子，其中e是自然对数的底。算法如下：

• 创建一个名为C的新空子集C = {}。
• 对于i从1到k：
• 选择S中的一个集合Si，该集合覆盖最多的新元素（即尚未被C中的集合覆盖的元素）。
• 将Si包含在C的子集中。
• 从集合S中移除Si。

虽然贪婪方法很简单并且有已证明的近似保证，但不能依靠它来获得理想的答案。虽然存在其他找到最佳解决方案的方法，例如整数线性规划，但它们通常比贪婪算法慢得多，特别是对于大的问题实例。

例如，n = 5, m = 4, k = 2

子集

2 1 2

2 2 3

2 3 4

2 4 5

以下详细信息在此输入中指定：

• 宇宙中有5个元素，编号从1到5。
• 有4个可用子集。
• 为了优化覆盖范围，我们必须选择正好2个子集。

以下定义了子集：

• 子集零：{1, 2}
• 子集一：{2, 3}
• 子集二：{3, 4}
• 子集三：{4, 5}

输出：选择的子集0 2

覆盖了四个元素。

说明

• 贪婪算法迭代k次，从一个空的已覆盖元素集合开始。
• 算法在第一次迭代中确定哪个子集具有最多的新元素来覆盖。目前所有子集的元素都未被覆盖。算法选择子集零（{1, 2}），因为它具有最多的元素。现在覆盖的元素列表是“1, 2”。
• 算法在第二次迭代中再次确定哪个子集具有最多的新元素来覆盖。剩余的子集是子集一、子集二和子集三。每个子集的新元素是：
• 子集一：{2, 3}（一个新元素，因为2已经提到）；
• 子集二：{3, 4}（一个新元素，因为3已经提到）；
• 子集三：{4, 5}（2个新元素）
• 算法选择子集二（{3, 4}），因为它包含最多的新元素（1）。现在覆盖的元素是1, 2, 3, 4。
• 算法运行k次迭代后，我们选择了子集零和子集二。这两个子集总共覆盖了四个元素。
• 输出显示覆盖的元素数量为“4”，选择的子集为“0 2”。

为什么要在最大覆盖中使用强制邻近限制？

因此，使用具有强制邻近限制的最大覆盖比位置集合覆盖问题能获得更令人满意的答案。

我们提出了时间约束最大覆盖销售员问题（TCMCSP），这是定向和覆盖销售员问题的一个扩展。在此问题中，中央仓库、客户和设施都表示为顶点，并且每个设施可以满足某些客户在指定覆盖区域内的需求。通过在设施子集上构建一个长度受限的哈密顿回路，从仓库开始，目标是最大化被覆盖的客户总数。针对研究问题，我们提供了几种数学规划模型，并随后提出了启发式方法。创建的算法使用了多种技术，如交换、删除、插入提取和扰动。最后，创建了一个基于整数线性规划的改进方法，以尝试提高解决方案的质量。通过对随机生成示例集合的大量计算机研究证明了该方法的有效性。

文献中描述了覆盖概念的众多现实世界应用。鉴于资源有限，在现实世界应用中满足所有客户的需求通常是不可能的。因此，在这种情况下，目标是提出最佳行动方案，同时考虑可用资源的限制，以最大化被覆盖的需求量。Church和ReVelle提出的最大覆盖位置问题（MCLP）要求我们考虑一组潜在的设施顶点和一组客户。

每个设施特别可以服务一定数量的客户，并在特定的服务半径（持续时间）内服务。目标是打开固定数量的设施（假设为p），以满足最大量的需求。后来，在1984年，Church提出了MCLP的平面示例，其中设施和客户顶点被认为是平面上的连续斑块，而不是离散的位置。研究人员已经开发出精确和启发式方法来解决这个问题。

我们提出的时间约束最大覆盖销售员问题（TCMCSP）是CSP和OP的自然扩展。在这个问题中，给出了一个中央仓库、多个设施和多个客户顶点，其中每个设施可以在其预定的覆盖区域（时间）内服务一部分客户。目标是构建一个长度（时间）受限的设施顶点子集上的哈密顿回路。它以仓库开始和结束，最大化被覆盖的客户总数。

上述问题的潜在应用存在于实际世界中。本质上，OP建议的某些用途可以应用于TCMCSP的实例。考虑移动电信网络中的每个塔，可以在服务固定数量客户位置的同时，同时服务多个需求区域。TCMCSP的实例，其目标是构建一个长度受限的塔子集回路，其中覆盖的总需求被最大化，可以通过OP的自然推广来扩展。在接下来的部分，我们为各种组合优化问题提供了几个TCMCSP应用。

所提出的问题可能出现在农村地区的医疗服务中，当需要迅速采取行动以阻止流行病或确保公众的安全和福祉时。假设一个医疗团队应该访问农村地区提供疫苗接种，并且每个地点的居民被鼓励前往最近的旅游站点。为了在预定时间内覆盖尽可能多的人，我们应该选择地点和访问顺序。

我们还可以讨论当一个地区的人口遭受自然或人为灾害（如地震或战争）时的情况，我们需要为他们提供食物、水和毯子等必需品。由于受伤者在没有基本药物或早期人道主义援助的情况下生命时间很短，我们应该尽快向他们提供供应品。因此，在这些应用程序中，我们需要在预定时间内最大化获得服务的客户数量。

考虑一个决定竞选公职的政治家。他可能只有很短的时间去不同的地方并提出他的计划。一些人可能会利用他的计划，因为不同的地点可能会为他带来相当不同的收益。应该访问哪些城市才能接触到最多的人，同时还要注意规定的时间？

例如，在25个单位的时间限制下，所提出的问题是在仓库开始和结束，访问四个设施顶点，并覆盖十一个客户。图中每条边的长度用其旁边的数字表示。

如何解决最多顶点问题？

此外，通过考虑在给定预算B的情况下覆盖至少q个顶点的类似问题，可以在多项式时间内解决在树上给定预算最大化覆盖顶点数的问题。后者可以改编以适应9 4中提出的类似算法。