Kosaraju 算法

2025年3月17日 | 阅读11分钟

在接下来的教程中，我们将学习强连通分量的形成以及如何使用 Kosaraju 算法找到它们。我们还将了解 Kosaraju 算法在 C++ 和 Python 等不同编程语言中的一些工作示例。

但在开始之前，让我们简要了解一下什么是强连通分量（SCC）。

理解强连通分量

如果图中任意一对节点（或顶点）之间都存在双向路径，则称该有向图是强连通的。这句话意味着存在从对中的第一个节点到第二个节点以及从第二个节点到第一个节点的路径。在一个可能不是强连通的有向图 G 中，如果节点 N 和 M 之间存在双向路径，则称它们是强连通的。

强连通性这个二元关系被认为是一个等价关系，其等价类的导出子图称为强连通分量（简称SCC）。等价地说，有向图 G 的强连通分量是一个强连通的子图，并且具有此特性的子图是极大的：G 中的其他节点或边不能包含在该子图中，而不会违反其强连通的特性。强连通分量的集合构成了 G 的节点集合的划分。如果一个强连通分量（SCC）只包含一个不与自身相连的节点，则称它是平凡的；否则，它被称为非平凡的。

现在，我们将通过一个例子来理解上面的内容

让我们考虑下图所示的图

图 1：初始有向图

上述图的强连通分量将是

图 2：有向图的强连通分量

正如我们从上图观察到的，第一个强连通分量中的每个节点都可以通过有向路径到达其他顶点。对于第二个和第三个强连通分量也可以得出类似的观察结果。

我们可以使用 Kosaraju 算法找到这些分量。

理解 Kosaraju 算法

Kosaraju 算法的核心是两次实现深度优先搜索算法。

该算法的完整过程分为以下步骤

步骤 1：首先，我们将对整个图进行深度优先搜索。

我们将从节点 A 开始，访问其所有子节点，并将选定的节点标记为已访问。如果节点指向一个已访问的节点，我们将当前节点推入堆栈。

图 3.1：给定的图

例如，在给定的图中，我们将从节点 0 开始，访问节点 1、节点 2，然后是节点 3。由于节点 3 指向一个已访问的节点，即节点 0，我们将源节点（即节点 3）推入堆栈。

图 3.2：图的 DFS

然后我们将回到前一个节点并访问其未访问的子节点，即依次是节点 4、节点 5、节点 6 和节点 7。由于我们无法从节点 7 进入任何地方，我们将它推入堆栈。

图 3.3：图的 DFS

现在我们将返回到前一个节点（即节点 6）并访问其子节点。但是，由于其所有子节点都已访问，我们将它推入堆栈。

图 3.4：堆叠

以类似的方式，创建最终的堆栈。

图 3.5：最终堆栈

步骤 2：反转原始图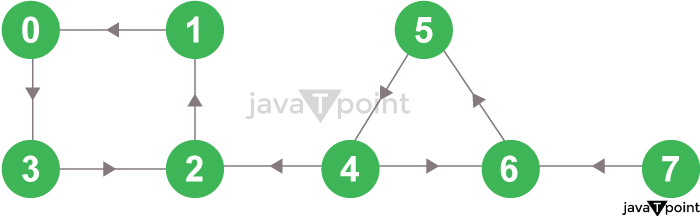

图 3.6：反转图的 DFS

步骤 3：对反转图进行深度优先搜索

现在我们将从堆栈的顶部节点开始，遍历其所有子节点。一旦达到已访问节点，就形成了一个强连通分量。

例如，我们将从堆栈中弹出节点 0。从节点 0 开始，我们将遍历其子节点（依次是节点 0、节点 1、节点 2、节点 3），并将它们标记为已访问，因此这些已访问节点构成了一个强连通分量。

图 3.7：从顶部开始遍历所有节点

现在我们将转到堆栈，如果顶部节点已访问，则弹出它。否则，我们将从堆栈中选择顶部节点并开始遍历其子节点，如给定图所示。

图 3.8：如果已访问，则弹出顶部节点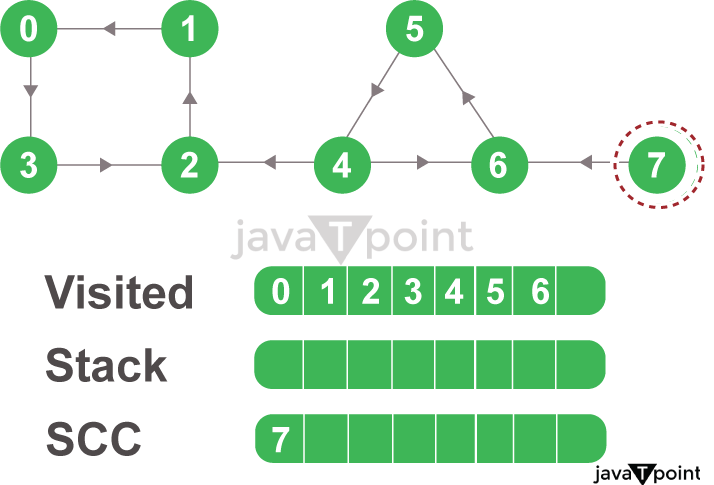

图 3.9：强连通分量

步骤 4：因此，图的强连通分量如下

图 3.10：所有强连通分量

在不同编程语言中实现 Kosaraju 算法

现在我们已经成功理解了 Kosaraju 算法的概念和工作原理，是时候看看它在 C++ 和 Python 等不同编程语言中的实现。

C++ 中 Kosaraju 算法的代码

以下是在 C++ 编程语言中实现 Kosaraju 算法

文件：example.cpp

// Kosaraju's Algorithm - Implementation in C++ to find strongly connected components

// including the required header files
#include <iostream>
#include <list>
#include <stack>

// using the standard namespace
using namespace std;

// defining the class
class DirectedGraph {
  // defining the required variables
  int N;  // number of variables
  list<int> *adj;   // empty list
  void fill_order(int a, bool visitedNodes[], stack<int> &Stack);  // method to push the elements in the stack
  void depth_first_search(int a, bool visitedNodes[]);   // method to perform depth first search   
   public:
    DirectedGraph(int N); // constructor for the graph creation
    void add_edge(int a, int d); // method to add edges into the graph
    void print_strongly_connected_components(); // method to print the strongly connected components
    DirectedGraph transpose(); // method to transpose nodes of the graph
};

// defining the constructor to create the graph
DirectedGraph :: DirectedGraph(int N) {
  this -> N = N;
  adj = new list<int>[N];
}

// defining the method to perform depth first search
void DirectedGraph :: depth_first_search(int a, bool visitedNodes[]) {
  visitedNodes[a] = true;
  cout << a << " ";

  list<int> :: iterator i;
  for (i = adj[a].begin(); i != adj[a].end(); ++i)
    if (!visitedNodes[*i])
      depth_first_search(*i, visitedNodes);
}

// defining the method to transpose nodes of the graph
DirectedGraph DirectedGraph :: transpose() {
  DirectedGraph graph(N);
  for (int a = 0; a < N; a++) {
    list<int>::iterator i;
    for (i = adj[a].begin(); i != adj[a].end(); ++i) {
      graph.adj[*i].push_back(a);
    }
  }
  return graph;
}

// defining the method to add edge into the graph
void DirectedGraph :: add_edge(int a, int d) {
  adj[a].push_back(d);
}

// defining the method to push elements into the stack
void DirectedGraph :: fill_order(int a, bool visitedNodes[], stack<int> &Stack) {
  visitedNodes[a] = true;

  list<int> :: iterator i;
  for (i = adj[a].begin(); i != adj[a].end(); ++i)
    if (!visitedNodes[*i])
      fill_order(*i, visitedNodes, Stack);

  Stack.push(a);
}

// defining the method print the strongly connected component
void DirectedGraph :: print_strongly_connected_components() {
  stack<int> Stack;

  bool *visitedNodes = new bool[N];
  for (int i = 0; i < N; i++)
    visitedNodes[i] = false;

  for (int i = 0; i < N; i++)
    if (visitedNodes[i] == false)
      fill_order(i, visitedNodes, Stack);

  DirectedGraph graph = transpose();

  for (int i = 0; i < N; i++)
    visitedNodes[i] = false;

  while (Stack.empty() == false) {
    int a = Stack.top();
    Stack.pop();

    if (visitedNodes[a] == false) {
      graph.depth_first_search(a, visitedNodes);
      cout << endl;
    }
  }
}

// main function
int main() {
  // instantiating the DirectedGraph() class to create a graph
  DirectedGraph graph(8);
  
  // adding edges to the graph
  graph.add_edge(0, 1);
  graph.add_edge(1, 2);
  graph.add_edge(2, 3);
  graph.add_edge(2, 4);
  graph.add_edge(3, 0);
  graph.add_edge(4, 5);
  graph.add_edge(5, 6);
  graph.add_edge(6, 4);
  graph.add_edge(6, 7);

  // printing a statement for the users
  cout << "The Strongly Connected Components of the Graph :\n";
  // calling the print_strongly_connected_components() method to print all the strongly connected components of the graph
  graph.print_strongly_connected_components();
}

输出

The Strongly Connected Components of the Graph :
0 3 2 1
4 6 5
7

说明

在上面的代码片段中，我们包含了必需的头文件并使用了标准命名空间。然后我们定义了一个名为 DirectedGraph 的类。在此类中，我们定义了一些变量和方法来服务于程序中的不同目的。然后我们定义了一个构造函数来为节点数量创建图。我们还定义了执行深度优先搜索的方法，我们将访问选定节点的所有子节点并将其标记为已访问。然后我们定义了转置图节点以反转其顺序的方法。我们还定义了在节点之间添加边以表示图中方向的方法。之后，我们定义了如果当前节点指向已访问节点则将其推入堆栈的方法。我们还定义了向用户打印图中所有强连通分量的方法。对于主函数，我们实例化了 DirectedGraph() 类并使用其 add_edge() 方法向图添加不同的边。最后，我们为用户打印了一个声明，并调用 print_strongly_connected_components() 方法来打印图中所有强连通分量。

结果，图中所有可能的强连通分量都为用户打印出来。

Python 中 Kosaraju 算法的代码

以下是在 Python 编程语言中实现 Kosaraju 算法

文件：example.py

# Kosaraju's Algorithm - Implementation in Python to find strongly connected components

# importing the defaultdict class from the collections module
from collections import defaultdict

# defining the class
class DirectedGraph:
    # defining an initializing method
    def __init__(self, nodes):
        # defining variables
        self.N = nodes     # number of nodes
        self.directed_graph = defaultdict(list)    # empty list

    # defining the method to add edge into the graph
    def addEdge(self, a, d):
        self.directed_graph[a].append(d)

    # defining the method to perform depth first search
    def depthFirstSearch(self, d, visited_nodes):
        visited_nodes[d] = True
        print(d, end = ' ')
        for i in self.directed_graph[d]:
            if not visited_nodes[i]:
                self.depthFirstSearch(i, visited_nodes)

    # defining the method to push elements into the stack
    def fillOrder(self, d, visited_nodes, stack):
        visited_nodes[d] = True
        for i in self.directed_graph[d]:
            if not visited_nodes[i]:
                self.fillOrder(i, visited_nodes, stack)
        stack = stack.append(d)

    # defining the method to transpose nodes of the graph
    def transpose(self):
        graph = DirectedGraph(self.N)

        for i in self.directed_graph:
            for j in self.directed_graph[i]:
                graph.addEdge(j, i)
        return graph

    # defining the method print the strongly connected components
    def printStronglyConnectedComponents(self):
        stack = []
        visited_nodes = [False] * (self.N)

        for i in range(self.N):
            if not visited_nodes[i]:
                self.fillOrder(i, visited_nodes, stack)

        graph = self.transpose()

        visited_nodes = [False] * (self.N)

        while stack:
            i = stack.pop()
            if not visited_nodes[i]:
                graph.depthFirstSearch(i, visited_nodes)
                print(" ")

# main function
if __name__ == '__main__':
    # instantiating the DirectedGraph() class to create a graph
    graph = DirectedGraph(8)

    # adding edges to the graph
    graph.addEdge(0, 1)
    graph.addEdge(1, 2)
    graph.addEdge(2, 3)
    graph.addEdge(2, 4)
    graph.addEdge(3, 0)
    graph.addEdge(4, 5)
    graph.addEdge(5, 6)
    graph.addEdge(6, 4)
    graph.addEdge(6, 7)

    # printing a statement for the users
    print("The Strongly Connected Components of the Graph :")
    # calling the printStronglyConnectedComponents() method to print all the strongly connected components of the graph
    graph.printStronglyConnectedComponents()

输出

The Strongly Connected Components of the Graph :
0 3 2 1
4 6 5
7

说明

在上面的代码片段中，我们从 collections 库导入了 defaultdict 类并定义了一个名为 DirectedGraph 的类。在此类中，我们定义了一个初始化方法来定义和初始化程序所需的一些变量。然后我们定义了在节点之间添加边以表示图中方向的方法。我们还定义了执行深度优先搜索的方法，我们将访问选定节点的所有子节点并将其标记为已访问。之后，我们定义了如果当前节点指向已访问节点则将其推入堆栈的方法。我们还定义了转置图节点以反转其顺序的方法以及向用户打印图中所有强连通分量的方法。对于主函数，我们实例化了 DirectedGraph() 类并使用其 addEdge() 方法向图添加不同的边。最后，我们为用户打印了一个声明，并调用 printStronglyConnectedComponents() 方法来打印图中所有强连通分量。

结果，图中所有可能的强连通分量都为用户打印出来。

理解 Kosaraju 算法的时间和空间复杂度

时间复杂度：在 Kosaraju 算法中，主要进行三个步骤

调用深度优先搜索：对图进行深度优先搜索（DFS）所需的时间，以邻接表为例，为O(V + E)。
反转以邻接表表示的图：要反转以邻接表表示的图，我们需要遍历邻接表，此过程所需的时间为O(V)。
再次调用深度优先搜索：对图进行深度优先搜索（DFS）所需的时间，以邻接表为例，为O(V + E)。

因此，在 Kosaraju 算法中执行上述三个步骤的总时间将是

O(V + E) + O(V) + O(V + E) = O(V + E)

因此，Kosaraju 算法的时间复杂度为O(V + E)，其中V是图中节点的数量，E是图中的边的数量。

空间复杂度：由于 Kosaraju 算法在执行第一次深度优先搜索（DFS）时使用堆栈存储节点，因此堆栈使用的空间等于图中节点的大小。

因此，Kosaraju 算法的空间复杂度为O(N)，其中N是图中的节点数量。

Kosaraju 算法的优缺点

Kosaraju 算法的优点在于我们可以轻松地使用深度优先搜索（DFS）实现它，并且它的时间复杂度为 O(V + E)，其中 V 是图中节点的数量，E 是图中的边的数量。
该算法的缺点是它需要将图及其转置存储在内存中，这对于大型图来说可能是一个问题。此外，该算法不适用于无向图，因为它只会识别属于单个强连通分量的所有节点。

强连通分量的应用

以下是强连通分量的一些应用

强连通分量（SCC）通常用于社交媒体算法，其中 SCC 用于了解具有共同兴趣和共同朋友的人。
强连通分量（SCC）也用于地图算法，以链接具有相似起点和终点的路径。
强连通分量（SCC）也用于车辆路线规划算法。

Kosaraju 算法的替代方案

除了 Kosaraju 算法之外，还有一些其他算法用于在有向图中查找强连通分量。这些算法的一些例子是Tarjan 算法和基于路径的强分量算法。

Tarjan 算法与 Kosaraju 算法相似，因为它也使用深度优先搜索（DFS）；但是，它使用不同的方法来识别图的强连通分量。
基于路径的强分量算法是一种较新的算法，它使用动态规划的方法来识别图的强连通分量。

结论

在上面的教程中，首先，我们理解了图的强连通分量的基本概念。
然后我们学习了 Kosaraju 算法及其工作原理。
之后，我们观察了它在 C++ 和 Python 等编程语言中的实现，并附有正确的输出和解释。
我们还理解了 Dijkstra 算法的时间和空间复杂度。
最后，我们讨论了 Dijkstra 算法的优缺点以及一些现实生活中的应用，并了解了它的替代方案。

下一个主题Floyd-Warshall 算法

Kosaraju 算法

理解强连通分量

理解 Kosaraju 算法

在不同编程语言中实现 Kosaraju 算法

C++ 中 Kosaraju 算法的代码

Python 中 Kosaraju 算法的代码

理解 Kosaraju 算法的时间和空间复杂度

Kosaraju 算法的优缺点

强连通分量的应用

Kosaraju 算法的替代方案

结论

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

DAA 教程

渐进分析

复发

排序分析

分而治之

排序

下界理论

线性时间排序

哈希

二叉搜索树

红黑树

动态规划

贪婪算法

回溯

最小生成树

最短路径

所有对最短路径

最大流

排序网络

复杂度理论

近似算法

字符串匹配

面试题

其他

Kosaraju 算法

理解强连通分量

理解 Kosaraju 算法

在不同编程语言中实现 Kosaraju 算法

C++ 中 Kosaraju 算法的代码

Python 中 Kosaraju 算法的代码

理解 Kosaraju 算法的时间和空间复杂度

Kosaraju 算法的优缺点

强连通分量的应用

Kosaraju 算法的替代方案

结论

相关帖子

算法的特点

Floyd 算法

交替奇偶校验的最大子数组和

Kruskals 算法的时间复杂度

如何编写算法

Kosaraju 算法

PageRank 算法

Dijkstra 算法

排序算法：最慢到最快

算法的属性

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器