最长重复子序列

最长重复子序列是指，在一个给定的字符串中，最长重复子序列的长度应该满足这样的条件：这两个子序列不能包含相同位置的字符，也就是说，给定的两个子序列中的第 i 个字符在原字符串中不能具有相同的索引。子序列是指通过从给定字符串中删除一个或多个元素而形成的新字符串。

目标： 用于查找最长重复子序列。它找出 LRS 的长度和 LRS 字符串。

约束： 两个子序列的第 i 个字符在字符串 S 中的索引不能相同。

示例 1

输入字符串：AAB

子序列 s1：A

子序列 s2：A

以上是两个长度为 1 的子序列。字符 'B' 不能包含在上述两个子序列中，因为它会在原字符串中位于相同的索引。

示例 2

输入字符串：AABB

子序列 s1：AB

子序列 s2：AB

以上是两个长度为 2 的子序列。在两个子序列中，'A' 在原字符串中的索引分别是第一个和第二个，'B' 在原字符串中的索引分别是第三个和第四个。

示例 3

输入字符串：AABEBCDD

子序列 s1：ABD

子序列 s2：ABD

以上是两个长度为 3 的子序列。在两个子序列中，'A' 在原字符串中的索引分别是第 1 个和第 2 个，'B' 在原字符串中的索引分别是第 3 个和第 5 个，'D' 在原字符串中的索引分别是第 7 个和第 8 个。

示例 4

输入字符串是：AABEBECDD

最长的重复子序列是“ABED”

最长的重复子序列的长度是 4。

示例 5

输入字符串是：“abcd”

由于没有字符出现两次以上，因此在上述给定的字符串中不存在重复子序列。

示例 6

输入字符串是：“bbc”

最长的重复子序列是 'b'，因为 'b' 重复了两次，并且我们不能包含 'c' 字符，因为它会在两个子序列中位于相同的索引。

示例 7

输入字符串是“a b x a y b c d c”

最长的重复子序列是“abc”，因为在两个子序列中；字符 'a'、'b' 和 'c' 在两个子序列中的索引是不同的。

最长重复子序列的长度是 3。

重要示例

输入字符串：A X X X

0 1 2 3

S：A X X X

子序列 s1：X X

1 2

子序列 s2：X X

2 3

正如我们在上述两个子序列中观察到的，对应字符在原字符串中具有不同的索引。因此，它们是有效的。

与 LCS 的相似性

考虑下面给出的字符串

S：AABBX

字符串中每个字符的索引如下

0 1 2 3 4

S：A A B B X

给定字符串的 LCS 将是

S：AABBX

给定字符串的 LRS 将是

S1：AB

S2：AB

以上是两个长度为 2 的子序列。在两个子序列中，'A' 在原字符串中的索引是不同的，即 S1 中 'A' 的索引是 0，S2 中 'A' 的索引是 1。字符 'B' 在两个子序列中的索引也是不同的，即 S1 中 'B' 的索引是 2，S2 中 'B' 的索引是 3。

LRS = LCS (排除相同索引处的字符)

注意：必须有多个字符实例才能贡献给 LRS。

查找排除相同索引处的字符的 LCS？

0 1 2

S1：X X X

S2：X X X

上述两个子序列是相同的，即 XXX。如果我们考虑 S1 中索引为 0 的 X 和 S2 中索引为 1 的 X，以及 S1 中索引为 1 的 X 和 S2 中索引为 2 的 X。那么，XX 将是最长的公共子序列，其长度最大，这也将是最长的重复子序列。LCS 和 LRS 的长度是 2。

算法

让我们进行一次干运行，找出排除相同索引处的字符的 LCS。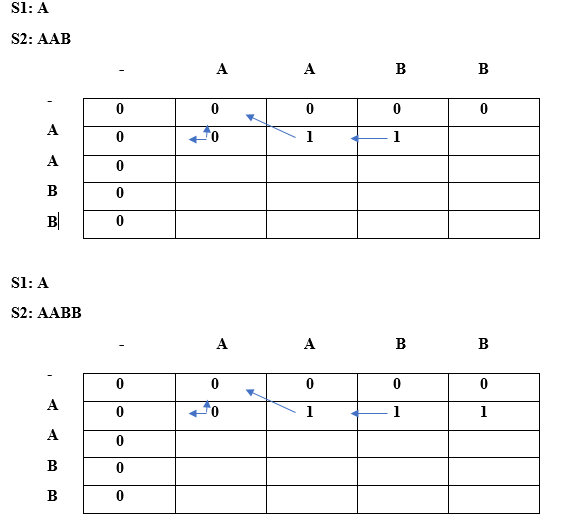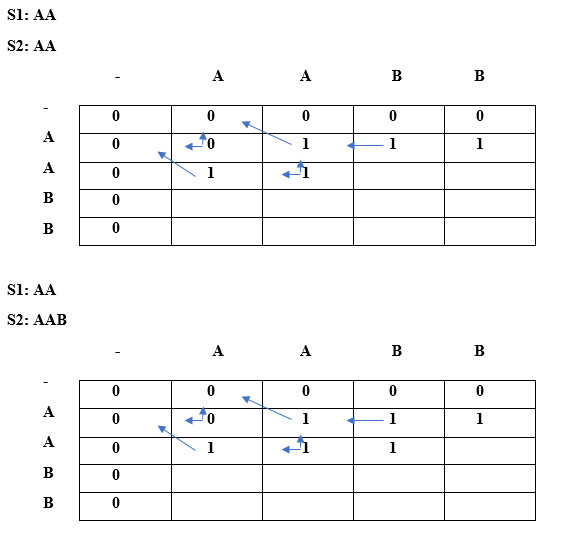

正如我们在上表中观察到的，最长重复子序列的长度是 2。

现在我们将找出 LRS 字符串。这里也将使用相同的算法。我们将 LCS 数组取为字符串类型，而不是整数类型。

首先，我们将在空字符串下方放入 '-'，如上表所示。

当 i = 0，j = 0 时

由于 lcs[i] = lcs[j]，即 'A'，并且 i==j，因此满足算法中的情况 3。因此，'-' 将出现在 lcs[0][0] 中，如下表所示。

当 i = 0，j = 1 时

由于 lcs[i]=lcs[j] 但 i!=j，因此满足情况 2。这里，lcs[0][1] = A + "" = A

由于 lcs[0]!= lcs[2]，因此我们将取顶部和左侧的最大值。

Lcs[0][2] = max(lcs[i-1][j], lcs[i][j-1])

Max(" ", 'A') // 最大值为 'A'，因此 lcs[0][2] 等于 'A'。

当 i = 0，j = 3 时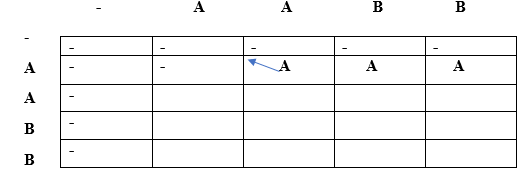

由于 lcs[0]!= lcs[3]，因此我们将取顶部和左侧的最大值。

Lcs[0][2] = max(lcs[i-1][j], lcs[i][j-1])

Max(" ", 'A') // 最大值为 'A'，因此 lcs[0][3] 等于 'A'。

当 i = 1，j = 0 时

由于 lcs[i] 等于 lcs[j]，即 'A'，但 i!=j，因此 lcs[1][0] 等于 (对角线元素 + 当前元素)。因此，lcs[1][0] 等于 (" " + 'A') = 'A'。

当 i = 1，j = 1 时

由于 lcs[i] = lcs[j]，即 A 且 i==j，因此满足算法中的情况 3。lcs[1][1] 将是顶部和左侧的最大值。顶部和左侧都是相同的，即 A，因此 lcs[1][1] 将等于 'A'。

当 i = 1，j = 2 时

由于 lcs[i] 不等于 lcs[j] 且 i 不等于 j，因此 lcs[i][j] 将是顶部和左侧的最大值。顶部和左侧都是相同的，即 A，因此 lcs[1][2] 将等于 'A'。

当 i = 1，j = 3 时

由于 lcs[i] 不等于 lcs[j] 且 i 不等于 j，因此 lcs[i][j] 将是顶部和左侧的最大值。顶部和左侧都是相同的，即 A，因此 lcs[1][2] 将等于 'A'。

当 i = 2，j = 0 时

由于 lcs[i] 不等于 lcs[j] 且 i 不等于 j，因此 lcs[i][j] 将是顶部和左侧的最大值。顶部和左侧都是相同的，即 A，因此 lcs[2][0] 将等于 'A'。

当 i=2，j=1 时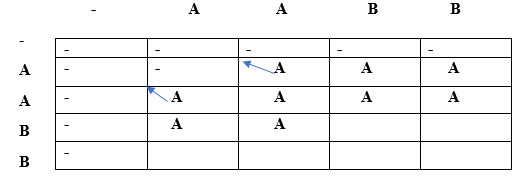

由于 lcs[i] 不等于 lcs[j] 且它们的索引也不同，因此满足情况 3。因此，lcs[2][1] 将是顶部和左侧的最大值。顶部和左侧都是相同的，即 A，因此 lcs[2][1] 将等于 'A'。

当 i = 2，j = 2 时

由于 lcs[i] 等于 lcs[j] 且 'i' 也等于 'j'，因此满足情况 3。因此，lcs[i][j] 将是顶部和左侧的最大值。顶部和左侧都是相同的，即 A，因此 lcs[2][2] 将等于 'A'。

当 i = 2，j = 3 时

由于 lcs[i] 等于 lcs[j] 且 'i' 不等于 'j'，因此满足情况 2。因此，lcs[2][3] 将等于 (对角线元素 + 当前元素) = A + B = AB。

类似地，我们将填充最后一行并得到如下表。

正如我们在上表中观察到的，AB 是最长的重复子序列。我们基本上是通过使用以下约束找到了 LCS：(i==j) 且 s[i] == s[j] 时，它将不贡献于重复子序列，否则它将贡献。