Longest Common Subsequence

这里的“最长”指的是子序列应该尽可能长。“公共”指的是两个字符串之间有一些共同的字符。“子序列”指的是从字符串中按顺序选取一些字符组成的序列。

让我们通过一个例子来理解子序列。

假设我们有一个字符串 'w'。

W₁ = abcd

从上面的字符串可以创建的子序列如下：

• ab
• bd
• ac
• ad
• acd
• bcd

以上都是子序列，因为子序列中的所有字符都相对于它们在原字符串中的位置是按递增顺序出现的。如果我们写 ca 或 da，那将是错误的子序列，因为字符不是按递增顺序出现的。可能的子序列总数为 2ⁿ，其中 n 是字符串中的字符数。在上面的字符串中，'n' 的值为 4，因此子序列的总数将是 16。

W₂= bcd

通过简单地查看两个字符串 w1 和 w2，我们可以说 bcd 是最长的公共子序列。如果字符串很长，那么就无法找到两个字符串的子序列并比较它们来找到最长的公共子序列。

使用动态规划通过表格来查找 LCS。

考虑两个字符串

X= a b a a b a

Y= b a b b a b

(a, b)

对于索引 i=1，j=1

由于两个字符都不同，我们取最大值。它们的值相同，即 0，所以在 (a,b) 处填入 0。假设我们从 'X' 字符串中取 0 值，那么我们将箭头指向 'a'，如上表所示。

(a, a)

对于索引 i=1，j=2

两个字符相同，因此该值将通过将 1 和左上角对角线的值相加来计算。这里，左上角对角线的值是 0，所以该项的值将是 (1+0) 等于 1。这里，我们考虑左上角对角线的值，所以箭头将指向对角线。

(a, b)

对于索引 i=1，j=3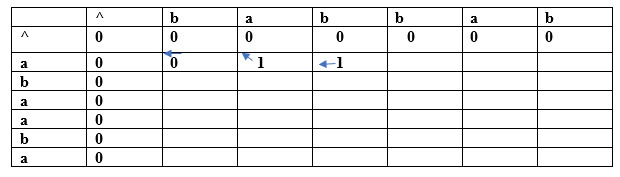

由于两个字符都不同，我们取最大值。字符 'a' 的最大值为 1。新项 (a, b) 将包含值 1，指向值为 1 的项。

(a, b)

对于索引 i=1，j=4

由于两个字符都不同，我们取最大值。字符 'a' 的最大值为 1。新项 (a, b) 将包含值 1，指向值为 1 的项。

(a, a)

对于索引 i=1，j=5

两个字符相同，因此该值将通过将 1 和左上角对角线的值相加来计算。这里，左上角对角线的值是 0，所以该项的值将是 (1+0) 等于 1。这里，我们考虑左上角对角线的值，所以箭头将指向对角线。

(a, b)

对于索引 i=1，j=6

由于两个字符都不同，我们取最大值。字符 'a' 的最大值为 1。新项 (a, b) 将包含值 1，指向值为 1 的项。

(b, b)

对于索引 i=2，j=1

两个字符相同，因此该值将通过将 1 和左上角对角线的值相加来计算。这里，左上角对角线的值是 0，所以该项的值将是 (1+0) 等于 1。这里，我们考虑左上角对角线的值，所以箭头将指向对角线。

(b, a)

对于索引 i=2，j=2

由于两个字符都不同，我们取最大值。字符 'a' 的最大值为 1。新项 (a, b) 将包含值 1，指向值为 1 的项。

就这样，我们将得到完整的表格。最终的表格将是

在上表中，我们可以看到所有项都已填满。现在我们位于最后一个单元格，值为 4。这个单元格向左移动，它包含值 4；因此，LCS 的第一个字符是 'a'。

左边的单元格向上对角线移动，值为 3；因此，下一个字符是 'b'，它变成 'ba'。现在单元格的值为 2，它向左移动。下一个单元格的值也是 2，它向上移动；因此，下一个字符是 'a'，它变成 'aba'。

下一个单元格的值为 1，它向上移动。现在我们到达单元格 (b, b)，其值向上对角线移动；因此，下一个字符是 'b'。最长公共子序列的最终字符串是 'baba'。

为什么动态规划方法解决 LCS 问题比递归算法更有效？

如果我们使用动态规划方法，那么函数调用的次数就会减少。动态规划方法会存储每个函数调用的结果，以便在将来的函数调用中可以使用这些结果，而无需再次调用函数。

在上面的动态算法中，比较 x 的元素和 y 的元素所得到的结果被存储在表中，以便将结果存储用于将来的计算。

动态规划方法完成表格所需的时间是 O(mn)，而递归算法所需的时间是 2^{max(m, n)}。

最长公共子序列算法

在 C 语言中实现 LCS 算法

输出