N皇后问题

N皇后问题是在一个n x n的棋盘上放置n个皇后，使得任何两个皇后都不能在同一行、同一列或同一对角线上相互攻击。

可以看出，当n=1时，问题有一个简单的解，而当n=2和n=3时，没有解。所以我们首先考虑4皇后问题，然后将其推广到n皇后问题。

给定一个4 x 4的棋盘，并为棋盘的行和列编号为1到4。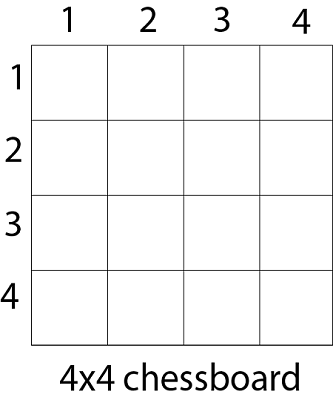

由于我们需要放置4个皇后，如q₁ q₂ q₃ 和 q₄ 在棋盘上，使得没有任何两个皇后相互攻击。在这种情况下，每个皇后必须放置在不同的行上，即，我们将皇后“i”放在第“i”行。

现在，我们将皇后q₁ 放在第一个可接受的位置 (1, 1)。接下来，我们放置皇后q₂ ，使这两个皇后不相互攻击。我们发现，如果我们将q₂ 放在第1列和第2列，那么就会遇到死胡同。因此，q₂ 的第一个可接受的位置在第3列，即 (2, 3)，但之后就没有位置可以安全地放置皇后 'q₃' 了。所以我们回溯一步，将皇后 'q₂' 放在 (2, 4) 上，这是下一个可能的最佳解决方案。然后我们得到放置 'q₃' 的位置，即 (3, 2)。但后来这个位置也导致了死胡同，并且找不到可以安全放置 'q₄' 的地方。然后我们必须回溯到 'q₁' 并将其放置到 (1, 2)，然后通过将q₂ 移动到 (2, 4)、q₃ 移动到 (3, 1) 和 q₄ 移动到 (4, 3) 来安全地放置所有其他皇后。也就是说，我们得到解决方案 (2, 4, 1, 3)。这是4皇后问题的一个可能的解决方案。对于另一个可能的解决方案，对所有部分解决方案重复整个方法。4皇后问题的另一个解决方案是 (3, 1, 4, 2) 即

4皇后问题的隐式树，对于一个解 (2, 4, 1, 3)，如下所示

图显示了4皇后问题的完整状态空间。但是我们可以使用回溯方法来生成必要的节点，如果下一个节点违反规则，即如果两个皇后相互攻击，则停止。

4 皇后解空间，节点按DFS编号

可以看出，4皇后问题的所有解都可以表示为 4 元组 (x₁, x₂, x₃, x₄)，其中x_i 表示皇后“q_i”所在的列。

图显示了8皇后问题的一个可能的解决方案

Place (k, i) 返回一个布尔值，如果第k个皇后可以放置在第i列，则为真。它测试 i 是否与所有先前的成本 x₁, x₂,....x_k-1 不同，以及是否有任何其他皇后在同一对角线上。

使用 place，我们给出了n皇后问题的精确解。

如果一个皇后可以放置在第k行和第i列，则 Place (k, i) 返回 true，否则返回 false。

x [] 是一个全局数组，其最终的 k - 1 个值已设置。Abs (r) 返回r的绝对值。